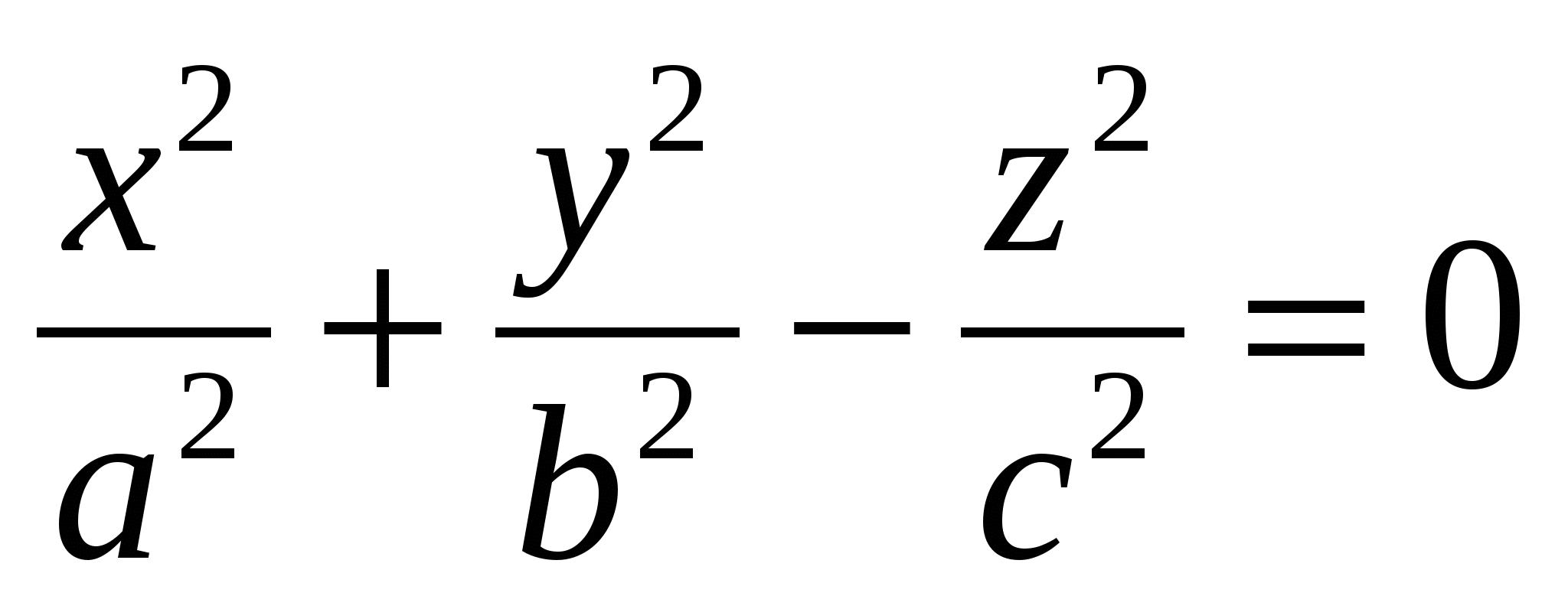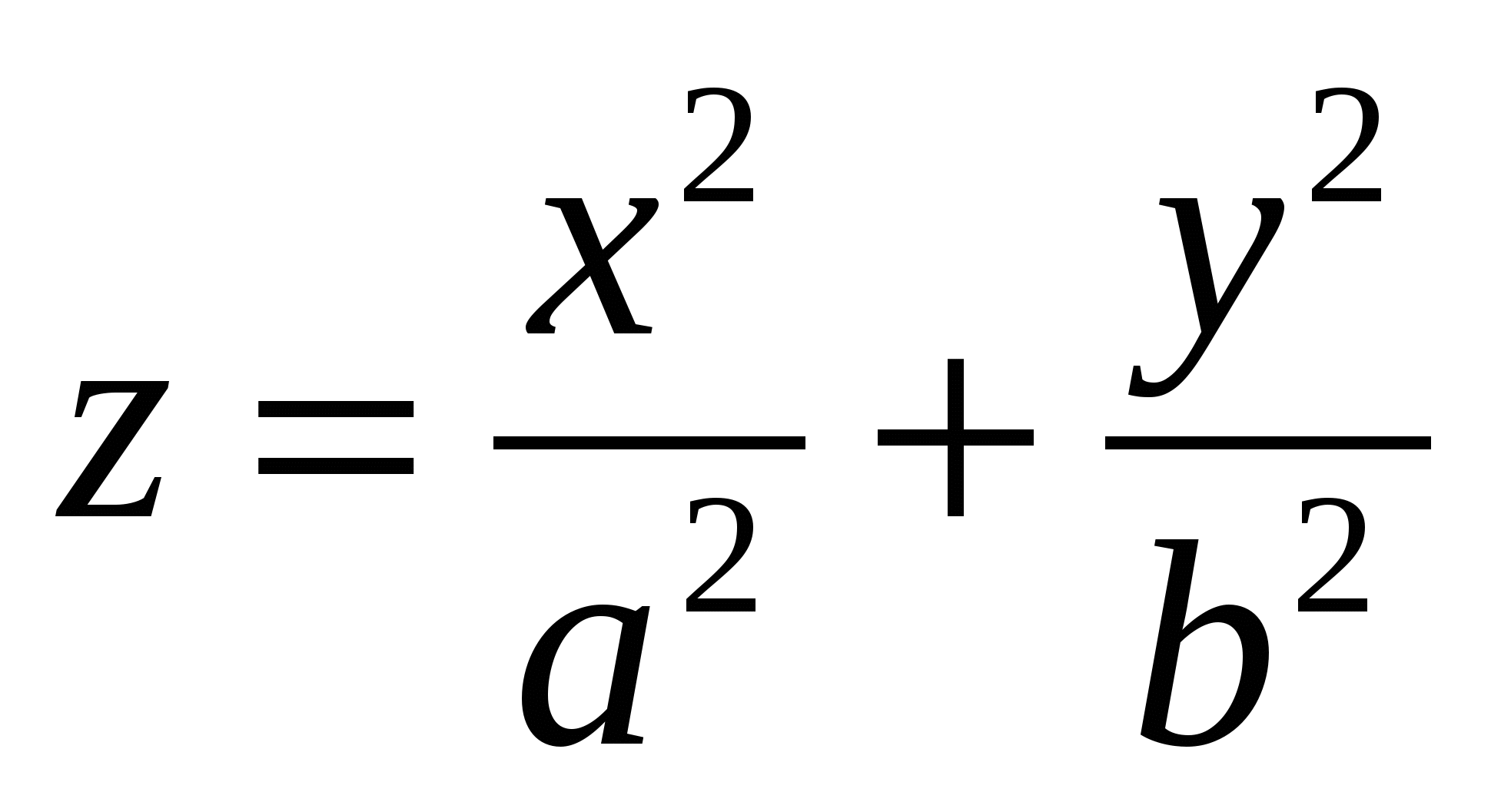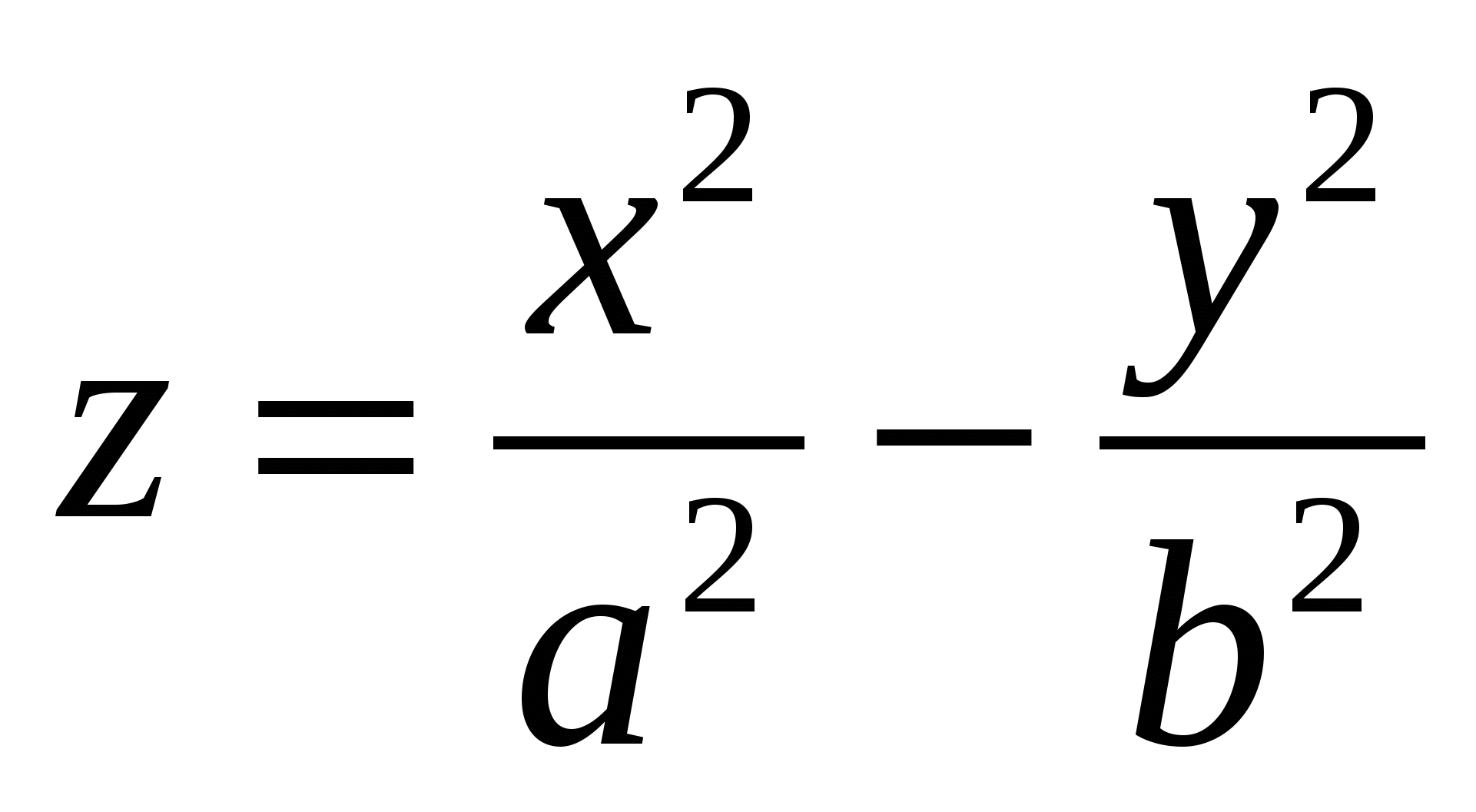|
|
Общее уравнение прямой, уравнение прямой по точке и нормальному вектору. Уравнение прямой в отрезкахОбщее уравнение прямой Уравнение прямой по точке и нормальному вектору A(x-x0)+B(y-y0)=0 Уравнение прямой в отрезках Уравнение прямой, проходящей через две данные точки
Уравнение прямой с угловым коэф. y=kx+b Нормальное уравнение прямой
Угол между двумя прямыми на плоскости. Условие параллельности и перпендикулярности двух прямых Угол между двумя прямыми на плоскости Условие параллельности Условие перпендикулярности двух прямых A1A2+B1B2=0
Плоскость в декартовой системе координат в пространстве Декартовыми прямоугольными координатами точки A в двумерном пространстве называются взятые с определенным знаком расстояния (выраженные в единицах масштаба) этой точки до двух взаимно перпендикулярных координатных осей или, что то же самое, проекции радиус-вектора r точки A на две взаимно перпендикулярные координатные оси.
Различные формы уравнений плоскости Уравнение плоскости по точке и нормальному вектору A(x-x0)+B(y-y0)+C(z-z0)=0 Общее уравнение плоскости Ax+By+Cz+D=0 Уравнение плоскости по трем точкам x-x1, y-y1, z-z1 X2-x1, y2-y1,z2-z1 =0 X3-x1, y3-y1, z3-z1 Уравнение плоскости в отрезках
Вычисления угла между плоскостями. Условия параллельности и перпендикулярности плоскостей
Условия параллельности Условия перпендикулярности плоскостей A1A2+B1B2+C1C2
Различные формы уравнений прямой в пространстве Векторное уравнение прямой r=r0+ts Параметрическое уравнение прямой X=x0+tm y=y0+tn z=z0+tp Каноническое уравнение Уравнение прямой, проходящей через 2 точки
Общее уравнение прямой в пространстве
Взаимное расположение прямой и плоскости Плоскости могут совпадать, быть параллельными или пересекаться по прямой. Прямая, параллельная плоскости. Прямая параллельна плоскости, если она параллельна прямой, лежащей в этой плоскости. Прямая, перпендикулярная к плоскости. Прямая линия перпендикулярна плоскости, если она перпендикулярна к любым двум пересекающимся прямым этой плоскости.
Общее уравнение кривой второго порядка. Определение типа кривой Линия, определенная уравнением Ax2+Bxy+Cy2+Dx+Ey+Q=0, называется кривой второго порядка
39.Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая. (x-x0)2+(y-y0)2= R2 Эллипс — геометрическое место точек M евклидовой плоскости, для которых сумма расстояний до двух данных точек F1 и F2 (называемых фокусами) постоянна и больше расстояния между фокусами, то есть F1M+F2M=2a причём F1F2<2a Окружность является частным случаем эллипса. Наряду с гиперболой и параболой, эллипс является коническим сечением и квадрикой.
Гипербола Геом.место точек в плоскости, для которой разность расстояний до 2 фиксированных точек плоскости называемых фокусами, есть постоянная величина.
Парабола —геометрическое место точек, равноудалённых от даннойпрямой (называемой директрисой параболы) и данной точки(называемой фокусом параболы). Y2= 2Px Общее уравнение поверхности 2го порядка
Цилиндрические поверхности — поверхность второго порядка, образуемая движением прямой (в каждом своём положении называемой образующей) вдоль кривой (называемой направляющей) так, что прямая постоянно остаётся параллельной своему начальному положению. В декартовых координатах может быть выражена уравнениями:
Сферойназывается геометрическое место точек пространства, равноудаленных от фиксированной точки, называемой центром. Сфера радиуса R с центром в точке Эллипсоидомназывается поверхность, каноническое уравнение которой имеет вид Однополостным гиперболоидомназывается поверхность, каноническое уравнение которой имеет вид Двуполостным гиперболоидомназывается поверхность, каноническое уравнение которой имеет вид Конусом второго порядка называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид Эллиптическим параболоидомназывается поверхность, уравнение которой в некоторой декартовой системе координат имеет вид Гиперболическим параболоидомназывается поверхность, уравнение которой в некоторой декартовой системе координат имеет вид
|
|


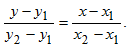


 =
=  =λ (в простейшем случае λ=1)
=λ (в простейшем случае λ=1) =
=  =
=  =1
=1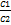
 =
=  =
= 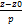
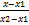 =
=  =
= 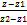
 +
+  =1
=1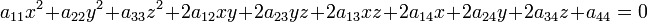

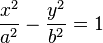
 имеет уравнение
имеет уравнение 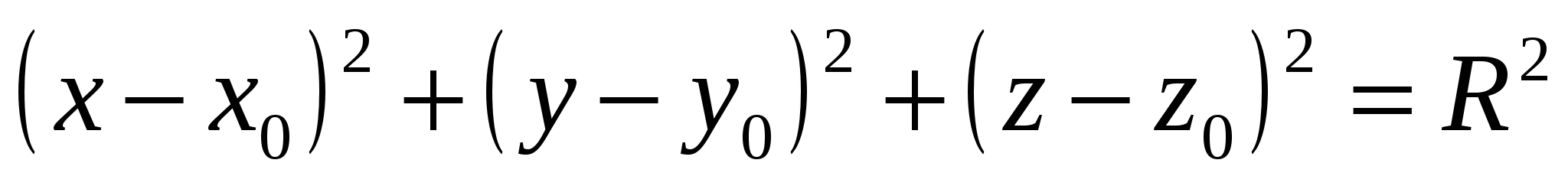
 , где a,b,c - положительные числа.
, где a,b,c - положительные числа.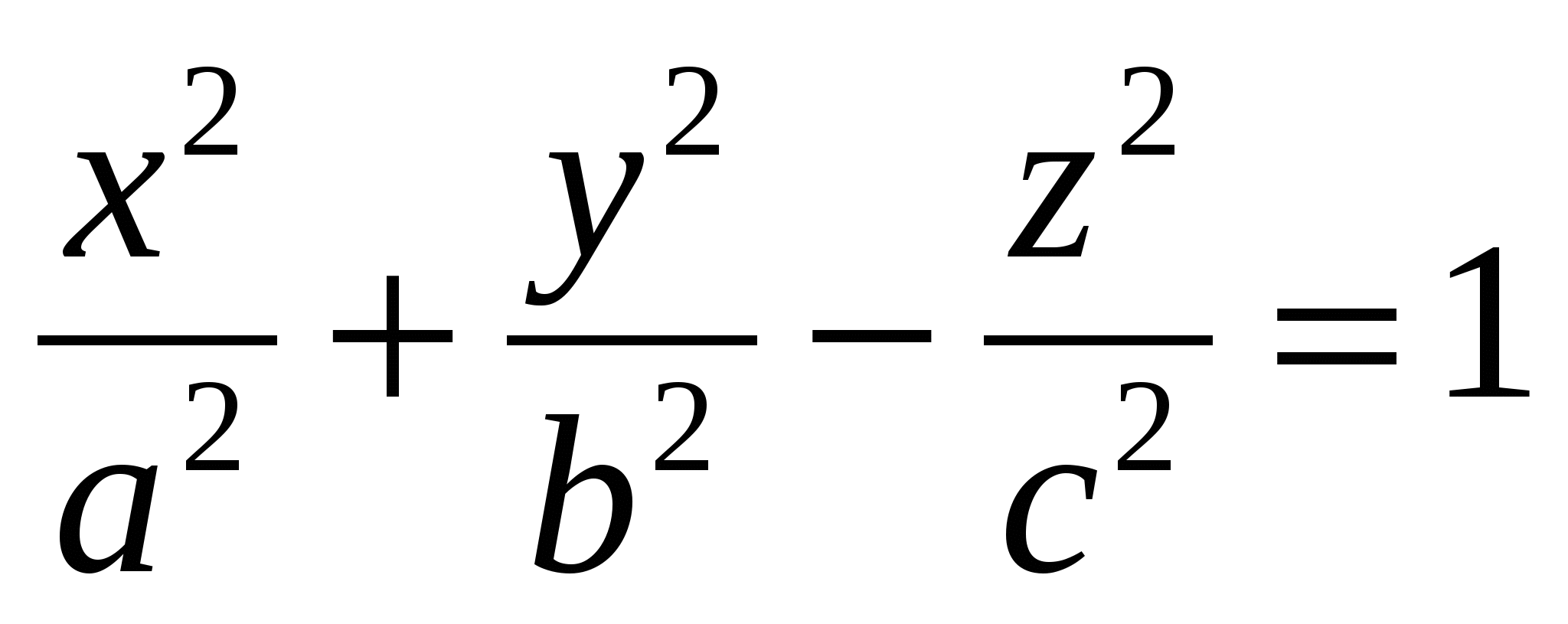 , где - положительные числа.
, где - положительные числа. , где - положительные числа.
, где - положительные числа.