|
|
Общие методические рекомендации к практическим занятиямЦель практических занятий по физике выражается в приобретении навыков использования теории для решения физических задач прикладного характера. Для этого на практических занятиях отбираются такие задачи, решение которых способствует усвоению основных разделов курса физики, углубляет представления о свойствах материи и объективном характере причинно-следственных связей в различных процессах. Подготовка к практическим занятиям состоит из частей, включающих в себя: самостоятельное изучение теории, соответствующей теме занятия; решение задач, предложенных на дом; подготовку к отчету по модулю. Для этого необходимо прочтение конспектов лекций и учебника; заучивание основных расчетных формул в соответствии с перечнем вопросов к занятию; понимание изученного физического явления; просмотр образцов решенных задач. Студентам следует порекомендовать примерную схему решения задач: 1. Начинайте с выявления данных задачи и ее неизвестных, которые нужно найти. Если план решения сразу не возникает, а вспомнить аналогичную задачу, решение которой вам было бы известно, вы не можете, то изобразите структуру задачи с помощью чертежа, схемы. Это позволит глубже понять структуру задачи, выявить возможность разбиения ее на подзадачи, и решить задачу по частям. 2. Если вы не можете осуществить поиск решения, сделайте перерыв, после чего приступите снова к задаче. Разбейте условие задачи на отдельные элементы и постарайтесь составить новую комбинацию этих элементов в сочетании с другими. 3. Если и в этом случае задача вам “не поддается”, то обратитесь за помощью к литературе и к преподавателю. Важно, чтобы вы предприняли самостоятельные попытки решения задачи, и довели решение задачи до конца. 4. После решения задачи сделайте проверку размерности полученной физической величины, сравните, если это возможно с табличными значениями, или решите задачу другим способом. Модуль I. Элементы квантовой механики. Экспериментальные основания квантовой физики. Занятие 1. Волновые свойства частиц. Соотношение неопределенностей. Краткие теоретические сведения Основные формулы Формула де Бройля, выражающая связь длины волны с импульсом а) в классическом приближении (
б) в релятивистском случае (скорость
Связь длины волны де Бройля с кинетической энергией а) в классическом приближении:
б) в релятивистском случае:
где Фазовая скорость волн де Бройля:
где Групповая скорость волн де Бройля:
Соотношения де Бройля:
где
Соотношения неопределенностей: а) для координаты и импульса частицы:
где б) для энергии и времени:
где Вопросы для ответа у доски: 1. В чем заключается корпускулярно-волновой дуализм материи? 2. Укажите волновые и корпускулярные характеристики света. 3. Запишите формулу связи между ними. 4. Изложите идею де Бройля о дуализме по отношению к движущимся частицам. 5. Приведите известные вам опыты по экспериментальному доказательству волновых свойств микрочастиц. 6. Запишите соотношение неопределенностей для координаты и импульса. 7. Дайте иллюстрацию этого соотношения на примере прохождения электронов через узкую щель. 8. Запишите и объясните соотношение неопределенностей для энергии и времени. 9. В чем, опираясь на соотношение неопределенностей, состоит отличие описания поведения частиц в классической и квантовой теориях? Примеры решения задач. Задача 1. Найти длину волны де Бройля для электрона, имеющего кинетическую энергию Решение. Так как Тогда
Длина волны равна
Подставив числовые значения, получим:
Ответ: Задача 2. Электрон начальной скоростью которого можно пренебречь, прошёл ускоряющую разность потенциалов 51 В и 510 кВ. Найти длину волны де Бройля для этих двух случаев. Решение. Длина волны де Бройля частицы определяется её импульсом согласно соотношению:
Импульс частицы можно определить, если известна её кинетическая энергия. Связь импульса с кинетической энергией различна для нерелятивистского случая (когда кинетическая энергия частицы много меньше её энергии покоя В нерелятивистском случае:
В релятивистском случае: Кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов определяется по формуле: В первом случае поэтому Во втором случае при ускоряющей разности потенциалов
Подставив числовые значения, получим:
Ответ: Задача 3. Используя соотношение неопределенностей энергии и времени, определить естественную ширину Решение. При переходе атомов из возбужденного состояния в основное существует некоторый разброс (неопределенность) в энергии испускаемых фотонов. Это связано с тем, что энергия возбужденного состояния не является точно определенной, а имеет конечную ширину Г (см рис.1).

Тогда ширина энергетического уровня: Вследствие конечной ширины уровня энергии возбужденного состояния энергия фотонов, испускаемых атомами, также имеет разброс, равный ширине энергетического уровня, т.е. Поскольку энергия фотона связана с длиной волны:
Конечный интервал длин волн Отсюда
Подставив числовые значения, получаем:
Ответ: Задача 4. Средняя кинетическая энергия электрона в невозбужденном атоме водорода равна 13,6 эВ. Исходя из соотношения неопределенностей, оценить наименьшую неточность определения координаты электрона в атоме. Решение. Согласно соотношению неопределенностей неточность
где величина неточности импульса неизвестна. Однако сам импульс (точнее его среднее квадратичное значение) легко найти, поскольку известна кинетическая энергия электрона. Рассматривая электрон как нерелятивистскую частицу, запишем:
Сравним величины
Подставив данные, получим, что Следовательно, наименьшая допустимая соотношением неопределенностей неточность, с которой можно определить координату электрона в атоме водорода, есть величина порядка Ответ: нельзя. Задача 5. Электронный пучок ускоряется в электронно-лучевой трубке разностью потенциалов 0,5 кВ. принимая, что неопределенность импульса электронов равна 0,1% его значения, определить неопределенность координаты электронов. Являются ли в данных условиях электроны квантовой или классической частицей? Решение. Согласно соотношению неопределенностей для координаты импульса: Кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов, Согласно условию задачи, неопределенность импульса Тогда искомая неопределенность координаты электрона
Ответ: Вопросы для самопроверки: 1. В чем суть и каковы результаты опытов Бибермана, Сушкина и Фабриканта с электронными пучками малой интенсивности? 2. Изложите суть и основные выводы мысленного эксперимента по рассеянию электронов на двух щелях. 3. Как понимать утверждение, что волны де Бройля имеют вероятностный характер? 4. Чему равны фазовая и групповая скорости фотона? 5. Физический принцип работы электронного и ионного микроскопов. 6.Что называется динамическими переменными? 7. Почему динамические переменные не могут быть приписаны микрообъектам? 8. Что такое неопределенность данной физической величины? 9. В каком случае и почему при условиях 10. Надо ли учитывать волновые свойства альфа-частицы, движущейся со скоростью 107 м/с, если ее положение оценивается по ширине следа в камере Вильсона (10-4м)? Задачи для самостоятельного решения: 1. Определить длину волны де Бройля 2. Найти длину волны де Бройля 3. Сравнить длину волны де Бройля для электрона и шарика массой 0,1 г, имеющих одинаковые скорости. 4. Вычислить и сравнить длины волн де Бройля для электрона и протона, прошедших ускоряющую разность потенциалов в 1000В. 5. Вычислить длину волны де Бройля для электрона, движущегося по круговой орбите атома водорода, находящегося в основном состоянии. 6. Вычислить длину волны де Бройля для протона с кинетической энергией 100 эВ. 7. Электрон движется по окружности радиусом 0,5 см в однородном магнитном поле с индукцией 8 мТл. Определить длину волны де Бройля для электрона. 8. Какую энергию необходимо дополнительно сообщить электрону, чтобы его дебройлевская длина волны уменьшилась от 0,1 нм до 0,05 нм? 9. Вычислить дебройлевские длины волн электрона, протона и атома урана, имеющих одинаковую кинетическую энергию 100эВ. 10. Вычислить длину волны де Бройля для электрона в кинескопе, ускоряющая разность потенциалов которого 10кВ. надо ли учитывать волновые свойства электрона, если диаметр электронного пучка 1 мм. 11. Вычислить длину волны де Бройля для пучка электронов в электронном микроскопе, ускоряющая разность потенциалов которого 1 кВ. Проявляются ли волновые свойства электронов, если объект бактерии, размер которых порядка 1 мкм? 12. Надо ли учитывать волновые свойства электронов в атоме водорода? Потенциал ионизации атома водорода 13,6 В, а размер атома порядка 0,53 10-10м. 13. Пучок альфа-частиц диаметром 1 см прошёл разность потенциалов 100В. надо ли учитывать волновые свойства альфа-частиц при распространении этого пучка? 14. Вычислить длину волны де Бройля для пучка протонов, имеющих скорость 103м/с. Надо ли учитывать волновые свойства, если диаметр пучка 1 мм? 15. Кинетическая энергия электрона равна 1 кэВ. Определить длину волны де Бройля. 16. Определить длину волны де Бройля для электрона, находящегося в атоме водорода на третьей боровской орбите. 17. Волновой «пакет» образован двумя плоскими монохроматическими волнами:
Определить фазовые скорости 18. Известно, что фазовая скорость 19. Фазовая скорость волн де Бройля больше скорости света в вакууме (в релятивистском случае). Не противоречит ли это постулатам теории относительности? 20. Написать закон дисперсии, т.е. формулу, выражающую зависимость фазовой скорости от длины волны) волн де Бройля в нерелятивистском и релятивистском случаях. 21. Будут ли расплываться в вакууме волновые пакеты, образованные из волн де Бройля? 22. Свободная частица движется со скоростью 23. Определить неточность 24. Пользуясь соотношением неопределенностей оценить неопределенность в определении скорости электрона атома водорода. Сравнить эту неопределенность с величиной скорости электрона на первой боровской орбите. Указать, применимо ли в данном случае понятие траектории. 25. Электрон с кинетической энергией 26. Во сколько раз дебройлевская длина волны 27. Кинетическая энергия электрона в атоме водорода составляет величину порядка 10 эВ. Используя соотношение неопределенностей оценить минимальные линейные размеры атома. 28. Если допустить, что неопределенность координаты движущейся частицы равна дебройлевской длине волны, то какова будет относительная неопределенность импульса этой частицы? 29. Используя соотношение неопределенностей 30. Показать, используя соотношение неопределенностей, что в ядре не могут находиться электроны. Линейные размеры ядра принять равными 5 фм. 31. Диаметр пузырька с жидкостно-водородной пузырьковой камере составляет величину порядка 0,1 мкм. Оценить неопределенность в определении скорости электрона и альфа-частицы, если неопределенность в определении координаты равна диаметру пузырька. 32. Оценить с помощью соотношения неопределенностей минимальную кинетическую энергию электрона, движущегося внутри сферической области диаметром 10 нм. 33. Оценить с помощью соотношения неопределенностей кинетическую энергию протона в моноэнергетическом пучке, используемом для исследования структуры с линейными размерами 10-10м. 34. Электрон движется со скоростью 106м/с. допустим, что мы можем измерить его положение с точностью до 10-12м. сравнить неопределенность импульса электрона с самим значением его импульса. 35. Теннисный мяч массой 200 г движется со скоростью 30 м/с. Если мы можем определить положение мяча с ошибкой, соизмеримой с длиной волны света, используемого при наблюдении (например, 500 нм), то, как соотносится неопределенность в установлении его импульса с самим импульсом мяча? 36. Оценить неопределенность импульса протона в ядре. Размер ядра 10-15м. 37. Определить отношение неопределенностей скорости электрона, если его координата установлена с точностью до 10 38. Электрон движется в атоме водорода по первой боровской орбите. Принимая, что допускаемая неопределенность скорости составляет 10% от её значения, определить неопределенность координаты электрона. Применимо ли в данном случае для электрона понятие траектории? 39. Пылинки массой 40. В потенциальном бесконечно глубоком одномерном ящике энергия 41. Какой смысл вкладывается в соотношение неопределенностей |
|
 движущейся частицы, для двух случаев:
движущейся частицы, для двух случаев: ):
):
 частицы сравнима со скоростью
частицы сравнима со скоростью 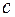 света в вакууме;
света в вакууме;  ):
):
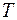 частицы:
частицы:

 энергия покоя частицы (
энергия покоя частицы ( 

 круговая частота;
круговая частота;  волновое число (
волновое число (  ).
).

 энергия движущейся частицы;
энергия движущейся частицы;  импульс частицы;
импульс частицы;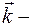 волновой вектор;
волновой вектор;  ;
; постоянная Планка (
постоянная Планка (  ).
).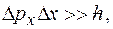
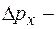 неопределенность проекции импульса частицы на ось
неопределенность проекции импульса частицы на ось  ;
;  неопределенность ее координаты;
неопределенность ее координаты;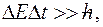
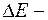 неопределенность энергии данного квантового состояния;
неопределенность энергии данного квантового состояния;  время пребывания системы в этом состоянии.
время пребывания системы в этом состоянии. эВ.
эВ. , то в данном случае электрон считается классической частицей.
, то в данном случае электрон считается классической частицей. отсюда импульс
отсюда импульс 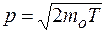



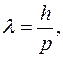 где
где  – постоянная Планка.
– постоянная Планка.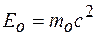 ) и для релятивистского случая (когда кинетическая энергия сравнима с энергией покоя частицы).
) и для релятивистского случая (когда кинетическая энергия сравнима с энергией покоя частицы). где
где  масса покоя электрона.
масса покоя электрона.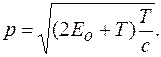

 и
и 
 (
(  ),
),
 кинетическая энергия 510 кэВ, что почти совпадает с энергией покоя 512 кэВ. Поэтому необходимо воспользоваться релятивистской формулой:
кинетическая энергия 510 кэВ, что почти совпадает с энергией покоя 512 кэВ. Поэтому необходимо воспользоваться релятивистской формулой:



 спектральной линии излучения атома при переходе его из возбужденного состояния в основное. Среднее время
спектральной линии излучения атома при переходе его из возбужденного состояния в основное. Среднее время 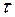 жизни атома в возбужденном состоянии принять равным 10-8 с, а длину волны
жизни атома в возбужденном состоянии принять равным 10-8 с, а длину волны  излучения – равной 600 нм.
излучения – равной 600 нм.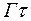 ~
~ 

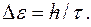
 то разбросу
то разбросу  энергии соответствует разброс
энергии соответствует разброс  :
: , (знак минус опущен).
, (знак минус опущен).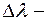 естественная ширина спектральной линии.
естественная ширина спектральной линии.


 координаты частицы:
координаты частицы:
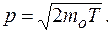
 и
и 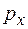 . Поскольку импульс вектор, то вычисляем только модуль этого вектора, так как его направление неизвестно. Поэтому проекция
. Поскольку импульс вектор, то вычисляем только модуль этого вектора, так как его направление неизвестно. Поэтому проекция  . Значит, неопределенность проекции импульса на ось х равна:
. Значит, неопределенность проекции импульса на ось х равна: т.е. величина
т.е. величина 
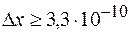 м.
м. м. Полученный результат сравним с диаметром первой боровской орбиты (
м. Полученный результат сравним с диаметром первой боровской орбиты (  м). Отсюда следует, что боровскую орбиту нельзя представить как траекторию, по которой движется электрон, так как он может оказаться в любом месте атома, находящегося в определенном состоянии.
м). Отсюда следует, что боровскую орбиту нельзя представить как траекторию, по которой движется электрон, так как он может оказаться в любом месте атома, находящегося в определенном состоянии.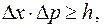 где
где 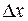 - неопределенность координаты электрона;
- неопределенность координаты электрона;  эВ, т.е. электрон при данных условиях является нерелятивистской частицей. Импульс электрона
эВ, т.е. электрон при данных условиях является нерелятивистской частицей. Импульс электрона 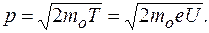
 кг·м/с.
кг·м/с.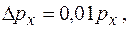 т.е.
т.е.  Поэтому электроны при данных условиях являются классическими частицами.
Поэтому электроны при данных условиях являются классическими частицами.

 и
и  можно говорить о движении частицы по определенной траектории?
можно говорить о движении частицы по определенной траектории? 1 Мм/с. Сделать такой же подсчет для протона.
1 Мм/с. Сделать такой же подсчет для протона.
 и
и  каждой волны и групповую скорость
каждой волны и групповую скорость  волнового «пакета».
волнового «пакета». Найти выражения фазовой скорости волн де Бройля в нерелятивистском и релятивистском случаях.
Найти выражения фазовой скорости волн де Бройля в нерелятивистском и релятивистском случаях.
 в определении скорости составляет 10% от ее величины. Сравнить полученную неточность с диаметром
в определении скорости составляет 10% от ее величины. Сравнить полученную неточность с диаметром  атома водорода, вычисленным по теории Бора для основного состояния, и указать, применимо ли понятие траектории в данном случае.
атома водорода, вычисленным по теории Бора для основного состояния, и указать, применимо ли понятие траектории в данном случае. 15 эВ находится в металлической пылинке диаметром
15 эВ находится в металлической пылинке диаметром 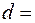 1 мкм. Оценить относительную неточность
1 мкм. Оценить относительную неточность  найти выражение, позволяющее оценить минимальную энергию
найти выражение, позволяющее оценить минимальную энергию 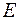 электрона, находящегося в одномерном потенциальном ящике шириной
электрона, находящегося в одномерном потенциальном ящике шириной 
 м, и пылинки массой 10
м, и пылинки массой 10  кг, если её координата установлена с такой же точностью.
кг, если её координата установлена с такой же точностью. 10-12 г взвешены в воздухе и находятся в тепловом равновесии. Можно ли установить, наблюдая за движением пылинок, отклонение от законов классической механики? Принять, что воздух находится при нормальных условиях, пылинки имеют сферическую форму. Плотность вещества, из которого состоят пылинки, равна 2·103 кг/м3.
10-12 г взвешены в воздухе и находятся в тепловом равновесии. Можно ли установить, наблюдая за движением пылинок, отклонение от законов классической механики? Принять, что воздух находится при нормальных условиях, пылинки имеют сферическую форму. Плотность вещества, из которого состоят пылинки, равна 2·103 кг/м3. ). С другой стороны, электрон заперт в ограниченной области с линейными размерами
). С другой стороны, электрон заперт в ограниченной области с линейными размерами  Не противоречит ли это соотношению неопределенностей?
Не противоречит ли это соотношению неопределенностей?