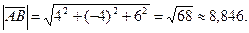|
|
Если орты образуют правую тройку, то система координат называется правой, если левую, то – левой.Мы будем работать только с правой системой координат (рис. 4.1). Определим понятие координат вектора. Рассмотрим произвольный вектор Определение 4.1.Координатамивектора
где
4.2. Разложение вектора по ортам. 10. Разложение вектора по ортам. Из прямоугольного параллелепипеда (рис. 4.1) следует:
Но
Равенство (4.3) и есть формула разложения вектора Таким образом, координатная запись вектора может быть осуществлена двумя способами:
20. Модуль вектора.Вектор
отсюда следует:
Модуль вектора равен корню квадратному из суммы квадратов его координат. Линейные операции над векторами. Сформулируем правила действий над векторами в координатной форме.
Пусть
Если
Покажем применение рассмотренного в этой главе материала к решению практической задачи. Задача 4.1.Даны векторы:
Найти: координаты и модуль вектора Решение. Используем координатную запись векторов и правила линейных операций над ними:
Модуль вектора
Ответ. Направляющие косинусы вектора
Выразим координаты вектора
С помощью данных равенств найдем выражения направляющих косинусов через координаты вектора
Вычислим сумму квадратов направляющих косинусов вектора
Полученный результат в векторной алгебре сформулирован в виде следующего утверждения: Сумма квадратов направляющих косинусов ненулевого вектора равна единице:
Задача 4.2. Определить направляющие косинусы вектора Решение. 10. Определим координаты и модуль вектора
20. Вычислим направляющие косинусы вектора
30. Проверим справедливость тождества (4.8):
Ответ. 4.5. Координаты точки в пространстве.
Определение 4.3.Радиус-вектором точки М называется вектор В качестве координат точки М примем координаты радиус-вектора. Определение 4.4.Координатами точки в пространстве называются координаты ее радиус-вектора. Координаты точки М (рис. 4.3) обозначаются символом:
Поставим задачу: найти координаты и модуль вектора
Координаты вектора равны соответствующим разностям координат конца и начала этого вектора. Задача 4.3. Даны две точки: Решение. Для определения координат вектора
По формуле (4.4) вычислим модуль вектора
Найдем направляющие косинусы вектора
Вычислим сумму квадратов направляющих косинусов:
Ответ.
|
|
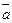 . Приведем его к началу координат, точке
. Приведем его к началу координат, точке  (рис. 4.1). Спроектируем этот вектор на координатные оси. Составляющими вектора
(рис. 4.1). Спроектируем этот вектор на координатные оси. Составляющими вектора  , а проекциями на координатные оси – числа
, а проекциями на координатные оси – числа  . Эти проекции носят названия координатами вектора.
. Эти проекции носят названия координатами вектора. на координатные оси. При этом пишут:
на координатные оси. При этом пишут: (4.1)
(4.1) Очевидно, координаты нулевого вектора равны 0:
Очевидно, координаты нулевого вектора равны 0: (4.2)
(4.2) .
.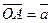 ,
,  ,
,  ,
,  , Следовательно,
, Следовательно,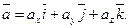 (4.3)
(4.3)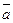 по ортам координатных осей.
по ортам координатных осей.
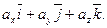
 ,
, , и наконец, получаем искомую формулу:
, и наконец, получаем искомую формулу: (4.4)
(4.4) . Координаты суммы (разности) векторов равны суммам (разностям) соответствующих координат этих векторов.
. Координаты суммы (разности) векторов равны суммам (разностям) соответствующих координат этих векторов.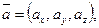
 тогда
тогда

 (4.5)
(4.5) При умножении вектора на скаляр его координаты умножаются на этот скаляр.
При умножении вектора на скаляр его координаты умножаются на этот скаляр.  – скалярная величина, то
– скалярная величина, то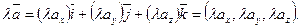 (4.6)
(4.6)




 вычислим по формуле (4.4):
вычислим по формуле (4.4):


 Определение 4.2.Направляющими косинусами ненулевого вектора называются косинусы углов, которые этот вектор образуют с осями координат (рис. 4.2).
Определение 4.2.Направляющими косинусами ненулевого вектора называются косинусы углов, которые этот вектор образуют с осями координат (рис. 4.2). :
: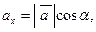


 (4.7)
(4.7)

 (4.8)
(4.8)
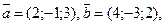 а также убедиться в справедливости тождества (4.8).
а также убедиться в справедливости тождества (4.8).







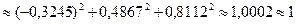

 Введем понятие координат точки в пространстве через понятие радиус-вектора.
Введем понятие координат точки в пространстве через понятие радиус-вектора. с началом в начале координат и концом в точке М, то есть вектор
с началом в начале координат и концом в точке М, то есть вектор  (рис. 4.3).
(рис. 4.3). , или
, или  . Таким образом,
. Таким образом,
 , если известны координаты его начала и конца:
, если известны координаты его начала и конца: 
 (рис. 4.4).
(рис. 4.4). Решение. Проведем в точки А и В радиус-векторы
Решение. Проведем в точки А и В радиус-векторы  и
и  , выразим координаты вектора
, выразим координаты вектора  и
и  (см. определение 4.4), получим:
(см. определение 4.4), получим: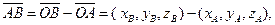
 (4.9)
(4.9) Найти координаты, разложение по ортам координатных осей, модуль и направляющие косинусы вектора
Найти координаты, разложение по ортам координатных осей, модуль и направляющие косинусы вектора