|
|
Свойства скалярного произведения
Это свойство используется для вычисления величины проекции одного вектора на другой в случае, когда векторы заданы своими координатами (об этом разговор позже).
Прежде чем формулировать следующее свойство, определим важное понятие. Определение 5.2.Скалярным квадратом вектора называется скалярное произведение вектора на себя. Скалярный квадрат вектора обозначается символом
Из равенства (5.6) следует:
Замечание. Из свойств скалярного умножения векторов следует, что преобразования векторных одночленов и многочленов относительно сложения, вычитания и умножения (в том числе и скалярного) можно производить по правилам преобразований алгебраических многочленов. Покажем это на примере решения задачи. Задача 5.1. Дано: Найти: Решение. По формуле (5.6*) получаем:
По формуле (5.5) имеем:
= Ответ.
5.3. Скалярное произведение векторов Свойства
Например, Таблица 5.1
Получим формулу скалярного произведения двух векторов в координатной форме. Имеем два вектора:
Перемножим их скалярно:
Учитывая данные таблицы, получаем:
Скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов. Из свойства
Для того чтобы два вектора были взаимно перпендикулярны, необходимо и достаточно чтобы сумма произведений соответствующих координат этих векторов была равна нулю. Рассмотрим две задачи, в которых используется формула (5.7). Задача 5.2. Найти проекцию вектора Решение.По свойству 10:
Ответ. Задача 5.3. Даны векторы: Найти скалярное произведение векторных двучленов: Решение.Решение задачи можно выполнить двумя способами: · перемножить двучлены, а затем представить векторы в координатной форме и выполнить действия; · сразу же представить векторы в координатной форме, и далее все действия осуществлять в этой форме. 10.Первый способ.
20.Второй способ.
Второй способ является, с нашей точки зрения, более рациональным. Ответ. Задача 5.4. Вычислить работу, которую производит сила Решение. Работа
Ответ. Угол между двумя векторами Для получения формулы угла между двумя векторами воспользуемся выражением скалярного произведения двух векторов:
отсюда получаем:
Подставляя в правую часть равенства (5.9) выражения
отсюда
Формула (5.11) и есть искомая формула угла между двумя векторами. Рассмотрим пример применения полученной формулы. Задача 5.5. Найти угол
Решение. Будем считать стороны Определим координаты векторов
По формулам (5.9) – (5.11) получаем:
Ответ. |
|
 Скалярное произведение двух векторов равно произведению модулей одного из них на проекцию другого вектора на этот вектор:
Скалярное произведение двух векторов равно произведению модулей одного из них на проекцию другого вектора на этот вектор: (5.2)
(5.2) Коммутативный (переместительный) закон:
Коммутативный (переместительный) закон: (5.3)
(5.3) Ассоциативный (сочетательный) закон относительно числового множителя:
Ассоциативный (сочетательный) закон относительно числового множителя: . (5.4)
. (5.4) Дистрибутивный (распределительный) закон:
Дистрибутивный (распределительный) закон: (5.5)
(5.5)
 Скалярный квадрат вектора
Скалярный квадрат вектора 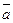 равен квадрату его модуля:
равен квадрату его модуля:
 (5.6)
(5.6) (5.6*)
(5.6*)


 и
и  .
.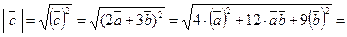


 ;
;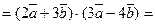

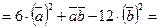


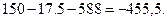
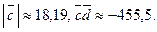
 Для того, чтобы векторы
Для того, чтобы векторы 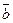 , были взаимно перпендикулярны, необходимо и достаточно, чтобы их скалярное произведение было равно нулю.
, были взаимно перпендикулярны, необходимо и достаточно, чтобы их скалярное произведение было равно нулю. Скалярное произведение ненулевых векторов
Скалярное произведение ненулевых векторов  и отрицательно при
и отрицательно при 
 и
и  позволяют получить скалярные векторов
позволяют получить скалярные векторов  – ортов координатных осей:
– ортов координатных осей:
 (по свойству 50);
(по свойству 50);  (по свойству 60), так как
(по свойству 60), так как  Аналогично обосновываются остальные соотношения. Результаты сведем в таблицу 5.1. В ней элементы главной диагонали – скалярные квадраты ортов, остальные элементы – парные произведения ортов. Таблица (табл. 5.1) скалярного умножения ортов представляет единичную матрицу третьего порядка.
Аналогично обосновываются остальные соотношения. Результаты сведем в таблицу 5.1. В ней элементы главной диагонали – скалярные квадраты ортов, остальные элементы – парные произведения ортов. Таблица (табл. 5.1) скалярного умножения ортов представляет единичную матрицу третьего порядка.
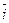
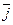
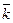
 ,
, 






 (5.7)
(5.7) скалярного произведения векторов и формулы (5.7) получаем условие перпендикулярности двух векторов в координатной форме:
скалярного произведения векторов и формулы (5.7) получаем условие перпендикулярности двух векторов в координатной форме: (5.8)
(5.8) на вектор
на вектор 
 если
если 


















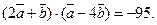
 , если точка ее приложения перемещается из начала в конец вектора
, если точка ее приложения перемещается из начала в конец вектора  , причем
, причем 

 силы
силы  на перемещении
на перемещении  Найдем координаты вектора
Найдем координаты вектора 
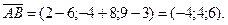




 (5.9)
(5.9) и
и  в координатной форме, получаем формулу угла между двумя векторами в координатной форме:
в координатной форме, получаем формулу угла между двумя векторами в координатной форме:
 (5.10)
(5.10) (5.11)
(5.11) треугольника
треугольника  , (рис. 5.2), вершины которого имеют координаты:
, (рис. 5.2), вершины которого имеют координаты:

 и
и  векторами
векторами  и
и  . Угол между этими векторами и есть угол
. Угол между этими векторами и есть угол  Найдем этот угол. Отметим, что векторы всегда должны иметь началом вершину того угла, величину которого мы определяем. В противном случае есть опасность определить не искомый угол, а смежный с ним угол.
Найдем этот угол. Отметим, что векторы всегда должны иметь началом вершину того угла, величину которого мы определяем. В противном случае есть опасность определить не искомый угол, а смежный с ним угол. и
и  :
:




