|
|
Агрегатная форма общего индекса
Основной формой общих индексов являются агрегатные индексы. Достижение в сложных статистических совокупностях сопоставимости разнородных единиц осуществляется введением в индексные отношения специальных сомножителей индексируемых величин. Такие сомножители называются соизмерителями. Они необходимы для перехода от натуральных измерителей разнородных единиц статистической совокупности к однородным показателям. При этом в числителе и знаменателе общего индекса изменяется лишь значение индексируемой величины, а их соизмерители являются постоянными величинами. В качестве соизмерителей индексируемых величин выступают тесно связанные с ними экономические показатели: цены, количество и др. Произведение каждой индексируемой величины на соизмеритель образует в индексном отношении определённые экономические категории. При определении общего индекса цен в агрегатной форме Агрегатная формула такого общего индекса цен имеет следующий вид:
Расчёт агрегатного индекса цен по данной формуле предложил немецкий экономист Г. Пааше, поэтому он называется индексом Пааше. При другом способе определения агрегатного индекса цен в качестве соизмерителя индексируемых величин В знаменателе индексного отношения образуется значение Агрегатная формула такого общего индекса имеет вид:
Расчёт общего индекса цен по данной формуле предложил немецкий экономист Э. Ласпейрес, и получил название индекса Ласпейреса. Индексы Пааше и Ласпейреса характеризуют различные качественные особенности изменения цен. Индекс Пааше характеризует влияние изменения цен на стоимость товаров, реализованных в отчётном периоде. Индекс Ласпейреса показывает влияние изменения цен на стоимость количества товаров, реализованных в базисном периоде. Другим важным видом общих индексов, которые широко применяются в статистике, являются агрегатные индексы физического объёма товарной массы. При определении агрегатного индекса физического объёма товарной массы Агрегатная форма общего индекса имеет следующий вид:
Поскольку, в числителе формулы 3 содержится сумма стоимости реализации товаров в текущем периоде по неизменным (базисным) ценам, а в знаменателе — сумма фактической стоимости товаров, реализованных в базисном периоде в тех же неизменных (базисных) ценах, то данный индекс является агрегатным индексом товарооборота в сопоставимых (базисных) ценах. Агрегатный индекс физического объёма товарооборота может определяться посредством использования в качестве соизмерителя индексируемых величин Агрегатная формула общего индекса будет иметь вид:
Аналогичным образом производится расчёт индекса себестоимости, при этом сравниваются суммы затрат в производстве в отчётном периоде ( В теории индексов обычно придерживаются следующего правила: · индексы качественных показателей строятся с весами отчетного периода (при этом в роли соизмерителей используется какой-либо количественный показатель); · индексы количественных показателей строятся с весами базисного периода (в этом случае соизмерителем служит какой-либо качественный показатель). Такое построение агрегатных индексов позволяет получить систему взаимосвязанных индексов и провести анализ влияния отдельных факторов на изменение обобщающих результативных показателей. Построим индексную модель, отражающую взаимосвязь динамики трех показателей – стоимости продукции, цен и количества реализованной продукции:
Такая модель называется мультипликативной. Мы получили систему взаимосвязанных агрегатных индексов, каждый из которых позволяет определить изменение индексируемого показателя в относительном выражении (%). Одна из задач индексного метода – анализ влияния отдельных факторов на изучаемое явление. Индексы рассматривают как показатели относительно изменения результативного показателя за счет отдельных факторов. Общее изменение стоимости продукции в абсолютном выражении исчисляется как разность между числителем и знаменателем общего индекса стоимости реализованной продукции:
Исходя из того, что на изменение стоимости продукции оказывают влияние два фактора (количество реализованной продукции и цены), приведем формулы расчета влияния каждого из этих факторов: · изменение стоимости реализованной продукции в абсолютном выражении за счет изменения цен исчисляется как разница между числителем и знаменателем индекса цен:
· изменение стоимости продукции в абсолютном выражении за счет изменения количества реализованной продукции исчисляется как разность между числителем и знаменателем индекса физического объема продукции:
Взаимосвязь исчисленных показателей:
Задача 1 Имеются следующие данные о продаже продукции:
На основе приведенных данных определить: 1) индивидуальные индексы цен и физического объема; 2) общие индексы цен, физического объема и товарооборота. 3) прирост товарооборота в целом и за счет изменения цен и физического объема.
РЕШЕНИЕ 1) индивидуальные индексы цен (характеризуют изменение цен по отдельным видам продукции)
р0 –цена базисного периода
А В С Следовательно, цена на продукцию «В» выросла на 13,0%; по продукции «А» и «С» снизилась на 6,5 и 1,6% соответственно.
Индивидуальные индексы физического объема (характеризуют изменение количества проданных отдельных видов продукции)
q0 – количество продукции базисного периода А В С Таким образом, количество проданной продукции «А» выросло в 1,5 раза, продукции «В» – на 67,6%, продукции «С» – на 40,0%.
2) Общий индекс цен (характеризует среднее изменение цен)
Цены на всю продукцию выросли в среднем на 5,0%.
Общий индекс физического объема
Количество проданной продукции в отчетном периоде по сравнению с базисным выросло на 55,7%.
Общий индекс товарооборота
Товарооборот вырос на 63,5%.
Взаимосвязь между исчисленными индексами:
1,635 = 1,050 * 1,557
3) Прирост товарооборота в целом:
а) за счет изменения цен:
б) за изменения физического объема
Взаимосвязь:
+ 2045 = + 249 + 1796
Вывод: В отчетном периоде по сравнению с базисным товарооборот вырос на 2045 тыс. руб., или на 63,5%; в том числе за счет роста цен товарооборот вырос на 249 тыс. руб., или на 5,0%; за счет увеличения объемов продаж товарооборот вырос на 1796 тыс. руб., или на 55,7%. Средневзвешенные индексы Помимо агрегатных индексов в статистике применяются средневзвешенные индексы.К их исчислению прибегают тогда, когда имеющаяся в распоряжении информация не позволяет рассчитать общий агрегатный индекс. Средний индекс - это индекс, вычисленный как средняя величина из индивидуальных индексов. Он должен быть тождествен агрегатному индексу. При исчислении средних индексов используются две формы средних: арифметическая и гармоническая. При построении средних индексов следует руководствоваться следующим правилом: для индекса количественного показателя обычно используют формулу среднего арифметического индекса, а для индекса качественного показателя – формулу среднего гармонического индекса. Среднеарифметический индекс физического объема продукции вычисляется по формуле:
Среднеарифметические индексы чаще всего применяются на практике для расчета сводных индексов количественных показателей. Средний гармонический индекс цен представляет собой среднюю гармоническую величину из индивидуальных индексов цен:
Имеются данные о продаже товаров в районе
Определите: 1) Общий индекс физического объёма товарооборота; 2) Абсолютный прирост стоимости проданных товаров за счёт изменения количества продажи товаров. Решение: 1) Определим общий индекс физического объёма товарооборота Ткани: iq = Iq = 2) Определим абсолютный прирост стоимости проданных товаров за счёт изменения количества продажи товаров (разница между числителем и знаменателем индекса физического объёма товарооборота) Iq = Товарооборот в отчётном периоде по сравнению с базисным возрос на 270 млн. руб. Индексы в форме средних из индивидуальных используют не только для характеристики изменения цен и физического объема, но и других (в основном, качественных) показателей: себестоимости, производительности труда, рентабельности и т.д. При этом должно выполняться основное требование – их тождественность агрегатному индексу и реальность весов как экономических категорий. Динамику среднего уровня качественного показателя для однородной совокупности изучают с помощью системы индексов переменного, постоянного состава и структурных сдвигов. Относительная величина, характеризующая динамику среднего уровня качественного показателя в однородной совокупности, называется индексом переменного состава. Он отражает влияние на изучаемый показатель двух факторов: изменения индексируемой величины у отдельных единиц совокупности и изменения структуры совокупности по изучаемому признаку. Индекс переменного состава для любых качественных показателей может быть построен следующим образом:
где х – индексируемая величина; f – вес индекса. Индекс постоянного (фиксированного) состава характеризует динамику среднего уровня качественного показателя при одинаковой фиксированной структуре совокупности. Другими словами, он показывает, как в среднем изменилось значение качественного показателя у единиц совокупности. В общем виде данный индекс можно записать следующим образом:
Индекс влияния структурных сдвигов представляет собой отношение средних величин рассматриваемого качественного показателя, рассчитанных при структуре совокупности отчетного и базисного периодов при постоянном значении качественного показателя. Формула индекса влияния структурных сдвигов:
Влияние структурных сдвигов на изменение среднего уровня изучаемого явления особенно заметно при сравнениях за длительные периоды времени и в условиях существенных изменений в структуре социально-экономических процессов. В связи с этим исключение воздействия структурного фактора при анализе изменений средних значений признаков как показателей основной тенденции – это необходимое условие для получения реалистичной оценки и правильных выводов на основе индексного анализа различных сложных явлений. Взаимосвязь индексов переменного, постоянного состава и влияния структурных сдвигов выражается уравнением:
На основе этих формул можно рассчитать абсолютное изменение среднего уровня вторичного признака за счет отдельных факторов – самого усредняемого признака и структуры. Имеются следующие данные о реализации яблок на рынках города:
На основе приведенных данных определить для трех рынков вместе: 1) индексы средней цены яблок переменного состава, постоянного состава и структурных сдвигов; 2) абсолютное изменение средней цены яблок по рынкам города в целом и за счет действия отдельных факторов.
РЕШЕНИЕ 1) Индекс переменного состава средней цены равен отношению средней цены отчетного периода к средней цене базисного периода
Индекс постоянного состава
Индекс структурных сдвигов
Взаимосвязь индексов:
2) Абсолютное изменение: Средней цены:
а) за счет изменения цен на отдельных рынках
б) за счет изменения в структуре продаж
Взаимосвязь: + 3,77 = + 3,79 – 0,02
Вывод: Средняя цена яблок выросла в декабре по сравнению с сентябрем на 3,77 руб., или на 15,3%, в том числе за счет роста цен на отдельных рынках – на 3,79 руб. За счет изменения структуры продаж средняя цена снизилась на 2 коп.
Цепные и базисные индексы В зависимости от выбора базы сравнения возможно построение системы цепных и базисных индексов. Индексы с переменной базой сравнения (цепные) получают путем сопоставления индексируемого показателя каждого последующего периода с показателем предшествующего ему периода. Индексы с постоянной базой сравнения (базисные) рассчитывают путем сравнения индексируемого показателя каждого периода с соответствующим показателем одного периода, принятого за базу сравнения. Индивидуальные цепные и базисные индексы, выраженные в относительных величинах, тождественны коэффициентам роста, используемым в системе показателей динамики. Для индивидуальных индексов справедливо следующее правило: · произведение промежуточных по периодам цепных индексов дает базисный индекс последнего периода; · отношение базисного индекса отчетного периода к базисному индексу предшествующего периода дает цепной индекс отчетного периода. Это правило позволяет применять цепной метод, т.е. находить неизвестный ряд базисных индексов по известным цепным, и наоборот. Для агрегатных индексов это правило действует только в отношении индексов, рассчитанных на основании постоянных весов. Пример. Известны следующие данные о реализации товаров в магазине.
Рассчитаем общие цепные индексы цен с переменными весами, характеризующие: 1) изменение цен в феврале по сравнению с январем:
2) изменение цен в марте по сравнению с февралем:
Вычислим общие цепные индексы физического объема проданных товаров с постоянными весами. За неизменные (сопоставимые) цены возьмем цены продажи товаров в январе. 1) изменение объема продаж в феврале по сравнению с январем:
2) изменение объема продаж в марте по сравнению с февралем:
|
|
 в качестве соизмерителя индексируемых величин
в качестве соизмерителя индексируемых величин  и
и  могут приниматься данные о количестве реализации товаров в текущем периоде
могут приниматься данные о количестве реализации товаров в текущем периоде  . При умножении
. При умножении  , сумма стоимости продажи товаров в текущем периоде по ценам того же текущего периода. В знаменателе индексного отношения образуется значение
, сумма стоимости продажи товаров в текущем периоде по ценам того же текущего периода. В знаменателе индексного отношения образуется значение 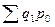 , т.е. сумма стоимости продажи товаров в текущем периоде по ценам базисного периода.
, т.е. сумма стоимости продажи товаров в текущем периоде по ценам базисного периода.
 (1)
(1) . При этом умножение
. При этом умножение  , т.е. сумму стоимости продажи товаров в базисном периоде по ценам текущего периода.
, т.е. сумму стоимости продажи товаров в базисном периоде по ценам текущего периода.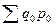 , т.е. сумма стоимости продажи товаров в базисном периоде по ценам того же базисного периода.
, т.е. сумма стоимости продажи товаров в базисном периоде по ценам того же базисного периода.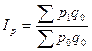 (2)
(2) в качестве соизмерителей индексируемых величин
в качестве соизмерителей индексируемых величин  (3)
(3) (4)
(4) — числитель индекса) с суммой затрат в производстве на продукцию отчётного периода по себестоимости базисного периода (
— числитель индекса) с суммой затрат в производстве на продукцию отчётного периода по себестоимости базисного периода (  — знаменатель).
— знаменатель). .
.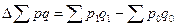 .
. ;
; .
. .
.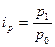 , где р1 – цена отчетного периода,
, где р1 – цена отчетного периода, , или 93,5%;
, или 93,5%; , или 113,0%;
, или 113,0%; , или 98,4%.
, или 98,4%. , где q1 – количество продукции отчетного периода,
, где q1 – количество продукции отчетного периода,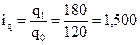 , или 150,0%;
, или 150,0%; , или 167,6%;
, или 167,6%; , или 140,0%.
, или 140,0%.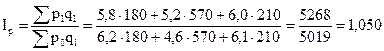 , или 105,0%.
, или 105,0%.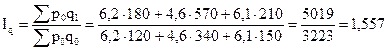 , или 155,7%.
, или 155,7%.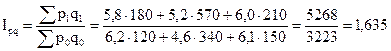 , или 163,5%.
, или 163,5%.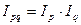
 5268 – 3223 = + 2045 тыс. руб.
5268 – 3223 = + 2045 тыс. руб.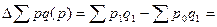 5268 – 5019 = + 249 тыс. руб.
5268 – 5019 = + 249 тыс. руб.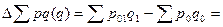 5019 – 3223 = + 1796 тыс. руб.
5019 – 3223 = + 1796 тыс. руб.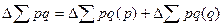
 .
. .
.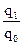 = 1, 1 или 110%
= 1, 1 или 110% = iq
= iq 
 или 110 %
или 110 % 770 – 2500 = 270 млн. руб.
770 – 2500 = 270 млн. руб. ,
, .
. .
.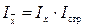
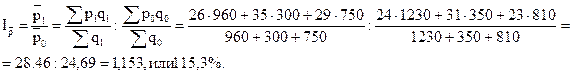
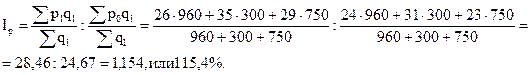
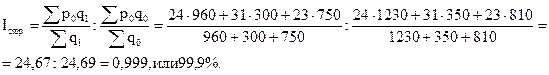
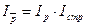 1,153 = 1,154 * 0,999
1,153 = 1,154 * 0,999 28,46 – 24,69 = + 3,77 руб.
28,46 – 24,69 = + 3,77 руб. 28,46 – 24,67 = + 3,79 руб.
28,46 – 24,67 = + 3,79 руб. 24,67 – 24,69 = – 0,02 руб.
24,67 – 24,69 = – 0,02 руб.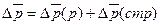
 ;
; .
. .
. .
.