|
|
Ошибки выборки. Задачи, решаемые при применении выборочного наблюденияРасхождение между значениями показателей, полученных по выборке, и соответствующими параметрами генеральной совокупности называют ошибкой репрезентативности. Различают систематические и случайные ошибки выборки. Случайные ошибки объясняются недостаточно равномерным представлением в выборочной совокупности различных категорий единиц генеральной совокупности. Систематические ошибки могут быть связаны с нарушением правил отбора или условий реализации выборки. Измерение ошибок репрезентативности выборочных показателей основано на предположении о случайном характере их распределения при бесконечно большом числе выборок. Количественную оценку надежности выборочного показателя используют, чтобы составить представление о генеральной характеристике. Это осуществляют либо на основе выборочного показателя с учетом его случайной ошибки, либо на основе выборочного показателя с учетом его случайной ошибки, либо на основе выдвижения некоторой гипотезы (о величине средней дисперсии, характере распределения, связи) в отношении свойств генеральной совокупности. Для проверки гипотезы оценивают согласованность эмпирических данных с гипотетическими. Величина случайной ошибки репрезентативности зависит: 1) от объема выборки; 2) степени вариации изучаемого признака в генеральной совокупности; 3) принятого способа формирования выборочной совокупности. Различают среднюю (стандартную) и предельную ошибки выборки. Средняя ошибка характеризует меру отклонений выборочных показателей от аналогичных показателей генеральной совокупности. Предельной ошибкой принято считать максимально возможное расхождение выборочной и генеральной характеристик, т.е. максимум ошибки при заданной вероятности ее появления. Зависимость величины ошибки выборки от способов формирования выборочной совокупности определяется по формулам средней ошибки выборки (табл. 2). Таблица 2 Формулы расчета средней ошибки выборки при различных способах отбора
Выборку считают безусловно большой при п > 100 и безусловно малой при п < 30. Среднюю ошибку малой выборки можно рассчитать по формуле
При серийном методе отбора с равновеликими сериями размеры вариации характеризуют межсерийные (межгрупповые) дисперсии: - средних ( - доли ( Они могут быть рассчитаны по следующим формулам:
где
где Для определения средней ошибки типической выборки в случае отбора единиц пропорционально численности каждой группы в качестве показателя вариации выступает средняя из внутригрупповых дисперсий ( Часто используют комбинированный отбор: индивидуальный отбор единиц сочетают с групповым, типический отбор – с отбором сериями. При любом способе отбора с определенной вероятностью можно утверждать, что отклонение выборочной средней (или доли) от генеральной средней (или доли) не превысит некоторую величину, которую называют предельной ошибкой выборки. Соотношение между пределом ошибки выборки (Δ), гарантируемым с некоторой вероятностью F(t), и средней ошибкой выборки имеет вид: Значения функции F(t) и t определяются на основе специально составленных математических таблиц. Приведем некоторые из них, применяемые наиболее часто:
Расчет средней и предельной ошибок выборки позволяет определить пределы, в которых будут находиться характеристики генеральной совокупности:
Пределы, в которых с данной степенью вероятности будет заключена неизвестная величина изучаемого показателя в генеральной совокупности, называют доверительным интервалом, а вероятность F(t) – доверительной вероятностью. Чем выше значение Δ, тем больше величина доверительного интервала и, следовательно, ниже точность оценки.
|
|





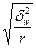



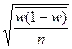

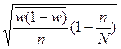
 .
. );
); ).
). ,
, - средняя i-й серии;
- средняя i-й серии;  - общая средняя по всей выборочной совокупности;
- общая средняя по всей выборочной совокупности; ,
, - доля единиц определенной категории в i-й серии;
- доля единиц определенной категории в i-й серии;  - доля единиц этой категории во всей выборочной совокупности; r – число отобранных серий.
- доля единиц этой категории во всей выборочной совокупности; r – число отобранных серий. - для количественного признака;
- для количественного признака;  - для альтернативного признака). По правилу сложения дисперсий величина средней из внутригрупповых дисперсий меньше, чем величина общей дисперсии. Значение средней возможной ошибки типической выборки меньше, чем ошибка простой собственно-случайной выборки.
- для альтернативного признака). По правилу сложения дисперсий величина средней из внутригрупповых дисперсий меньше, чем величина общей дисперсии. Значение средней возможной ошибки типической выборки меньше, чем ошибка простой собственно-случайной выборки. , где t – коэффициент доверия, определяемый в зависимости от уровня вероятности F(t).
, где t – коэффициент доверия, определяемый в зависимости от уровня вероятности F(t). ;
;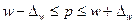 .
.