|
|
Тангенціальне і нормальне прискорення. Зв’язок між кінематичними величинами криволінійного руху.1.1. Кінематика руху матеріальної точки. Системи координат. Переміщення і швидкість руху. Пройдений шлях. Середні значення кінематичних величин
Кінематикою називають розділ механіки, в якому вивчається рух тіл без вияснення причин цього руху. Механічним рухом тіла називають зміну його положення в просторі по відношенню до інших тіл протягом певного часу. Механічний рух є відносним. Рух одного і того ж тіла відносно різних тіл може бути різним. Тому для пояснення руху тіла слід вказувати тіло відліку, тобто тіло, відносно якого розглядається рух в просторі й часі. З тілом відліку зв’язують систему координат.
Системою координат називають три взаємно перпендикулярні осі, початок яких суміщається з тілом відліку. Таку систему координат називають декартовою. Положення довільної точки М в просторі характеризується радіусом-вектором З рисунку видно, що
де
Рис.1.1
Рух матеріальної точки М(x,y,z) повністю буде визначено, якщо декартові координати матеріальної точки будуть задані в залежності від часу: x = x(t); y=y(t); z=z(t) . (1.1.3)
Ці рівняння називаються кінематичними рівняннями руху точки, вони еквівалентні одному векторному рівнянню руху
Будь-яке тіло має відповідні розміри. Тому різні частини тіла можуть перебувати в різних точках простору. Якщо розміри тіла малі в порівнянні з відстанями до інших тіл, то дане тіло можна вважати матеріальною точкою. Якщо всі частини тіла рухаються однаково, то такий рух називається поступальним. Прикладом поступального руху може бути рух автомобіля на горизонтальній ділянці шляху. При поступальному русі тіла його можна розглядати як матеріальну точку. Поняття матеріальної точки відіграє дуже важливу роль, значно спрощуючи розуміння кінематику руху матеріальної точки. Переміщуючись у просторі з однієї точки в іншу, тіло описує деяку лінію, яку називають траєкторією руху тіла. Рівняння траєкторії руху можна одержати, якщо з кінематичних рівнянь (1.1.3) виключити час t. У залежності від форми траєкторії, рух матеріальної точки, або твердого тіла, може бути прямолінійним і криволінійним. При прямолінійному русі вектор переміщення збігається з напрямком руху, а при криволінійному русі напрям вектора переміщення може бути під довільним кутом до напрямку руху. Довжина шляху точки визначається сумою довжин всіх ділянок траєкторії, пройденої точкою за відповідний проміжок часу t. DS=DS(t). (1.1.5)
Довжина шляху – скалярна функція часу.
Переміщенням точки
Рис.1.2
З рис. 1.2 видно, що
де Якщо час Dt руху точки від А до В прямує до нуля, то довжина шляху DS буде наближатися до довжини вектора переміщення.
Для характеристики руху матеріальної точки вводиться поняття середньої швидкості
Вектором середньої швидкості за час Dt називається відносне переміщення У кінематиці руху більше уваги приділяється не середній швидкості, а миттєвій. Миттєва швидкість визначається границею, до якої наближається відношення (1.1.7) за безмежно малий проміжок часу, тобто
Вектор миттєвої швидкості збігається з дотичною до траєкторії руху і направлений в сторону руху. Модуль миттєвої швидкості є скалярною величиною і дорівнює першій похідній шляху за часом
звідки
Якщо рух нерівномірний, то вводять поняття модуля миттєвоїшвидкості, величина якої змінюється з часом. В цьому випадку середню швидкість нерівномірного руху визначають за формулою:
Довжина шляху S, пройденого точкою за проміжок часу від t1 до t2, визначається інтегралом
При прямолінійному русі точки напрям вектора швидкості залишається незмінним. Рух точки називається рівномірним, якщо модуль її швидкості не змінюється з часом. Для такого руху
S=uDt. (1.1.12)
Якщо модуль швидкості збільшується з часом, то такий рух називається прискореним, якщо ж він зменшується, то він називається сповільненим. Прискорення- це векторна величина, яка характеризує швидкість зміни швидкості по модулю і за напрямком. Середнє прискорення матеріальної точки в інтервалі часу Dt є векторною величиною, рівною відношенню зміни швидкості
Миттєве прискорення матеріальної точки в інтервалі часу
|
|
 , який з’єднує початок координат з точкою М в просторі (рис.1.1).
, який з’єднує початок координат з точкою М в просторі (рис.1.1). , (1.1.1)
, (1.1.1) - одиничні вектори, напрямки яких збігаються з напрямками відповідних осей координат x, y, z. Модуль радіуса-вектора дорівнює
- одиничні вектори, напрямки яких збігаються з напрямками відповідних осей координат x, y, z. Модуль радіуса-вектора дорівнює . (1.1.2)
. (1.1.2)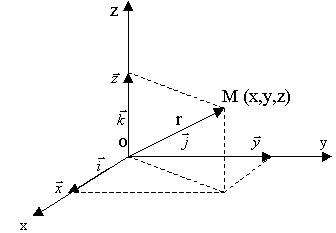
 . (1.1.4)
. (1.1.4) називають спрямований відрізок прямої, який з’єднує початкове положення точки з його наступним положенням. Переміщення точки є векторною величиною (рис.1.2).
називають спрямований відрізок прямої, який з’єднує початкове положення точки з його наступним положенням. Переміщення точки є векторною величиною (рис.1.2).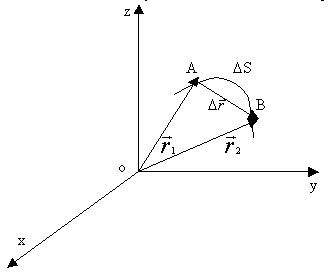
 , (1.1.6)
, (1.1.6) - радіус-вектор точки А,
- радіус-вектор точки А,  -радіус-вектор точки В.
-радіус-вектор точки В. . (1.1.7)
. (1.1.7) радіуса-вектора точки до проміжку часу Dt. Одиницею вимірювання швидкості є м/с.
радіуса-вектора точки до проміжку часу Dt. Одиницею вимірювання швидкості є м/с. . (1.1.8)
. (1.1.8) , (1.1.9)
, (1.1.9) .
. . (1.1.10)
. (1.1.10) (1.1.11)
(1.1.11) =const, a
=const, a за час Dt:
за час Dt: =
= 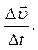 (1.1.13)
(1.1.13) визначається похідною вектора швидкості за часом:
визначається похідною вектора швидкості за часом: . (1.1.14)
. (1.1.14)