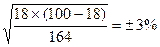|
|
Определение доверительных границ средних и относительных величин.Формулы определения доверительных границ представлены следующим образом: · для средних величин (М): Мген=Мвыб ± tm · для относительных показателей (Р): Рген=Рвыб ± tm где Мген и Рген - соответственно, значения средней величины и относительного показателя генеральной совокупности; Мвыб и Рвыб – значения средней величины и относительного показателя выборочной совокупности; m- ошибка репрезентативности; t- критерий достоверности (доверительный коэффициент). Данный способ применяется в тех случаях, когда по результатам выборочной совокупности необходимо судить о размерах изучаемого явления (или признака) в генеральной совокупности. Обязательным условием для применения способа является репрезентативность выборочной совокупности. Для переноса результатов, полученных при выборочных исследованиях, на генеральную совокупность необходима степень вероятности безошибочного прогноза (Р), показывающая, в каком проценте случаев результаты выборочных исследований по изучаемому признаку (явлению) будут иметь место в генеральной совокупности. При определении доверительных границ средней величины или относительного показателя генеральной совокупности, исследователь сам задает определенную (необходимую) степень вероятности безошибочного прогноза (Р). Для большинства медико-биологических исследований считается достаточной степень вероятности безошибочного прогноза, равная 95 %, а число случаев генеральной совокупности, в котором могут наблюдаться отклонения от закономерностей, установленных при выборочном исследовании, не будут превышать 5%. При ряде исследований, связанных , например, с применением высокотоксичных веществ, вакцин, оперативного лечения и т.п., в результате чего возможны тяжелые заболевания, осложнения, летальные исходы, применяется степень вероятности Р=99,7 %, т.е. не более чем у 1% случаев генеральной совокупности возможны отклонения от закономерностей , установленных в выборочной совокупности. Заданной степени вероятности (Р) безошибочного прогноза соответствует определенное, подставляемое в формулу, значение критерия t, зависящее также и от числа наблюдений. При n>30 степени вероятности безошибочного прогноза Р=99,7% -- соответствует значение t= 3, а при Р=95,5 % - значение t=2. При n<30 величина t при соответствующей степени вероятности безошибочного прогноза определяется по специальной таблице (Н.А. Плохинского). Задача-эталон на определение ошибок репрезентативности (m) и доверительных границ средней величины генеральной совокупности (Мген) при числе наблюдений больше 30 Условие задачи: при изучении комбинированного воздействия шума и низкочастотной вибрации на организм человека, было установлено, что средняя частота пульса у 36 обследованных водителей сельскохозяйственных машин через 1 час работы составила 80 ударов в 1 минуту; σ= ± 6 уд. в мин. Задание: определить ошибку репрезентативности (mм) и доверительные границы средней величины генеральной совокупности (М ген).
Решение 1. Вычисление средней ошибки средней арифметической (ошибки репрезентативности) (m):
2. Вычисление доверительных границ средней величины генеральной совокупности (Мген). Для этого необходимо: а) задать степень вероятности безошибочного прогноза (Р=95 %). б) определить величину критерия t. При заданной степени вероятности (Р=95%) и числе наблюдений меньше 30 величина критерияt, определяемого по таблице, равна 2 (t=2). ТогдаМген=Мвыб± tm =80±2х1=80±2 удара в мин. Вывод: установлено с вероятностью безошибочного прогноза Р= 95%, что средняя частота пульса в генеральной совокупности, т.е. у всех водителей сельскохозяйственных машин, через 1 час работы в аналогичных условиях будет находиться в пределах от 78 до 82 ударов в минуту, т.е. средняя частота пульса менее 78 и более 82 ударов в минуту возможна не более, чем у 5% случаев генеральной совокупности.
Задача-эталон на определение ошибок репрезентативности (m) и доверительных границ относительного показателя генеральной совокупности (Рген)
Условие задачи: при медицинском осмотре 164 детей 3-х летнего возраста, проживающих в одном из районов г. Н, в 18% случаев обнаружено нарушение осанки функционального характера. Задание: определить ошибку репрезентативности (mР) и доверительные границы относительного показателя генеральной совокупности (Р ген).
Решение Вычисление ошибки репрезентативности относительного показателя:
2. Вычисление доверительных границ средней величины генеральной совокупности (Рген): производится следующим образом: а) необходимо задать степень вероятности безошибочного прогноза (Р =95%). б) при заданной степени вероятности и числе наблюдений больше 30, величина критерия tравна2 (t=2). ТогдаРген=Рвыб± tm =18%±2х3 = 18%±6%. Вывод: установлено с вероятностью безошибочного прогноза Р=95%, что частота нарушения осанки функционального характера у детей 3-х летнего возраста, проживающих в г. Н., будет находиться в пределах от 12% до 24% случаев.
|
|
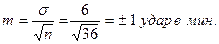
 =
=