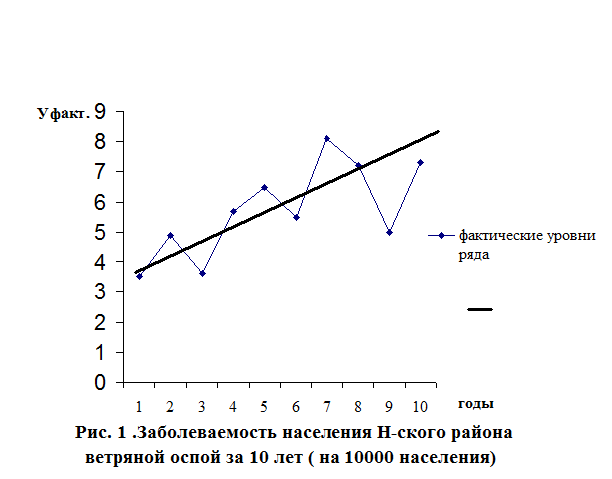
Заболеваемость населения Н-ского района ветряной оспой за 10 лет

(на 10 000 населения)

Задание: На основании данного динамического ряда требуется:

1. Обосновать необходимость выравнивания ряда.

2. Выровнять ряд по способу наименьших квадратов;

3. Рассчитать показатели динамического ряда (абсолютный прирост, темп прироста, средний темп прироста, значение 1% прироста);

4. Изобразить ряд графически;

5. Сделать выводы о динамике явления по выровненным уровням,

6. Охарактеризовать скорость изменения заболеваемости.

Решение

а = S У_ф. / n = 57,3 / 10 = 5,73 УХ ₉₇ = 5,73 + 0,179 х (-9) = 4,119

в = S (Х У_факт.) / S Х² = 59,2 / 330 = 0,179 УХ ₉₈ = 5,73 + 0,179 х (-7) = 4,477

УХ ₉₉ = 5,73 + 0,179 х (-5) = 4,835

Абсолютный прирост выровненного ряда – 4,477-4,119 = 0,358

Темп прироста для 1997 г. = (0,358 / 4,119) х 100 = 8,69 %

Темп прироста для 1998 г. = (0,358 / 4,477) х 100 = 7,99 %

Темп прироста для 1999 г. = (0,358 / 4,835) х 100 = 7,4 %

Средний темп прироста = (0,179 х 2 / 5,73) х 100 = 6,24 %

Абсолютный прирост = 4,477 – 4,119 = + 0,358

Значение 1% прироста = + 0,358 / 6,24 = 0,057 %.

Выводы: Заболеваемость населения Н-ского района ветряной оспой за 10 лет неравномерна. Скорость изменений показателей заболеваемости различна, наибольший темп прироста отмечается в 1998 году. При выравнивании показателей динамического ряда отмечается тенденция к увеличению уровней заболеваемости, в среднем на 6,24 % ежегодно.

Контрольные вопросы

1. Дайте определение динамического ряда.

2. Какие Вы знаете типы динамических рядов?

3. Что такое преобразование динамического ряда?

4. Какие Вы знаете методы выравнивания динамического ряда?

5. Какой из методов выравнивания является боле точным?

6. Какие показатели свидетельствуют о скорости изменений уровней динамического ряда?

Задача 1

При анализе ежемесячной заболеваемости скарлатиной детей в возрасте до 7 лет в городе Н. в изучаемом году были получены следующие показатели динамического ряда: абсолютный прирост = + 0,5, темп прироста = +8,0%; темп роста = 7,0%.

1. По каким из представленных показателей можно судить о скорости изменения заболеваемости во времени?

2. Достаточно ли представленных в условии задачи данных для Вашего заключения о необходимости срочного планирования мероприятий по снижению заболеваемости скарлатиной на следующий год?

Задача 2

За последнее десятилетие отмечается увеличение числа выпуска врачей различного профиля в медицинских вузах №1 и №2, особенно увеличился выпуск в позапрошлом и прошлом годах.

Показатели динамики выпуска врачей вуза № 1 за последний год составили: абсолютный прирост = 50 человек, темп прироста = +8 %, а вуза № 2 за последний год - абсолютный прирост = 60 человек, темп прироста = 10 %.

1. Можно ли сделать вывод, что вуз № 2 более быстро решает проблему недостаточной численности подготовленных врачей? Какими показателями Вы воспользовались?

2. Достаточно ли представленных данных в условии задачи для суждения о приоритете в тенденциях по подготовке врачей в вузах?

Задача 3

В условиях реформирования здравоохранения в районах А. и Б. было проведено сокращение коечного фонда с увеличением при этом объема внебольничной помощи. 1% снижения (убыли) коечного фонда в районе А. составил 2 %, в районе Б. – 3%, а средний темп снижения (убыли) – соответственно– 5% и 7,5%.

1. В каком из районов сокращение коечного фонда идет быстрее. На основании какого показателя Вы сделали этот вывод?

2. Какие еще показатели дополнят анализ процесса сокращения коечного фонда в 2-х районах?

Задача 4

В городе Н. численность населения за последние 5 лет составляла в динамике:

1-й год - 100 00 человек, 2-й год - 90 000 , 3-й год - 80 000, 4-й год - 70 000 и 5-й год - 60 000 человек. Обеспеченность врачами за этот же период составила соответственно: 25, 23, 24, 18 и 20 на 10000 населения.

1. Являются ли исходные данные основой для составления динамического ряда и его последующего анализа?

2. Какие показатели динамического ряда необходимо рассчитать для углубленного анализа изменений численности населения и обеспеченности врачами?

Список литературы

Основная:

1.Власов В.В. Эпидемиология. - М.: ГЭОТАР-МЕД, 2004. - 464.

2.Лисицын Ю.П. Общественное здоровье и здравоохранение. Учебник для вузов. – М.:ГЭОТАР – МЕД, 2002.- 520 с.

3.Медик В.А., Юрьев В.К. Курс лекций по общественному здоровью и здравоохранению: Часть 1. Общественное здоровье. - М.: Медицина, 2003. - 368 с.

4.Социальная медицина и организация здравоохранения (Руководство в 2-х томах). Миняев В.А., Вишняков Н.И. и др. - СПб, 1998. - 528 с.

5.Социальная гигиена и организация здравоохранения (Учебное пособие). Кучеренко В.З., Агарков Н.М. и др. – Москва, 2000. – 432 с.

Глава 5. Дисперсионный анализ

Введение

В практической деятельности врачей при проведении медико-биологических, социологических и экспериментальных исследований возникает необходимость установить влияние факторов на результаты изучения состояния здоровья населения, при оценке профессиональной деятельности, эффективности нововведений.

Для определения влияния факторов существует ряд статистических методов, позволяющих определить силу, направление, закономерности влияния факторов на результат в генеральной или выборочной совокупностях (расчет критерия t, корреляционный анализ, регрессия, χ² (критерий согласия Пирсона) и др.).

Дисперсионный анализ был разработан и предложен английским ученым, математиком и генетиком Рональдом Фишером в 20-х годах XX века.

Дисперсионный анализ чаще используют в научно-практических исследованиях общественного здоровья и здравоохранения для изучения влияния одного или нескольких факторов на результативный признак, - он также устанавливает силу влияния фактора (ов) в выборочных совокупностях и основан на принципе «отражения разнообразий значений факторного(ых) на разнообразии значений результативного признака».

Сущность метода дисперсионного анализа заключается в измерении отдельных дисперсий (общая, факториальная, остаточная), и дальнейшем определении силы (доли) влияния изучаемых факторов (оценки роли каждого из факторов, либо их совместного влияния) на результативный (е) признак.

Цель изучения темы

На основе применения однофакторного дисперсионного анализа уметь оценивать силу и достоверность влияния фактора на результат.

По окончании изучения данной темы студент должен:

Уметь:

· обосновывать применение дисперсионного анализа в проводимом исследовании;

· проводить расчет показателей по этапам;

· на основании полученных данных проводить анализ полученных данных;

· формулировать практические выводы о влиянии факторов и их достоверности на состояние здоровья населения и /или деятельность учреждений здравоохранения.

Знать:

· основные понятия дисперсионного анализа;

· условия применения дисперсионного анализа;

· виды дисперсионного анализа;

· применяемые критерии для оценки полученных результатов.

Задания для самостоятельной работы студента

Изучить материалы обязательной и рекомендуемой литературы, данного раздела учебного пособия.

1. Рассмотреть алгоритм применения дисперсионного анализа на примере решения задачи- эталона.

2. Ответить на контрольные вопросы и тестовые задания.

3. Решить ситуационные задачи.

Блок информации

Дисперсионный анализ- это статистический метод оценки связи между факторными и результативным признаками в различных группах, отобранным случайным образом, основанный на определении различий (разнообразия) значений признаков. В основе дисперсионного анализа лежит анализ отклонений всех единиц исследуемой совокупности от среднего арифметического. В качестве меры отклонений берется дисперсия (D)– средний квадрат отклонений. Отклонения, вызываемые воздействием факторного признака (фактора) сравниваются с величиной отклонений, вызываемых случайными обстоятельствами. Если отклонения, вызываемые факторным признаком, более существенны, чем случайные отклонения, то считается, что фактор оказывает существенное влияние на результативный признак. Для того, чтобы вычислить дисперсию значения отклонений каждой варианты (каждого зарегистрированного числового значения признака) от среднего арифметического возводят в квадрат. Тем самым избавляются от отрицательных знаков. Затем эти отклонения (разности) суммируются и делят на число наблюдений, т.е. усредняют отклонения. Таким образом, получают значения дисперсий.

Важным методическим значением для применения дисперсионного анализа является правильное формирование выборки. В зависимости от поставленной цели и задач выборочные группы могут формироваться случайным образом независимо друг от друга (контрольная и экспериментальная группы для изучения некоторого показателя, например, влияние высокого артериального давления на развитие инсульта). Такие выборки называются независимыми. Нередко результаты воздействия факторов исследуются у одной и той же выборочной группы (например, у одних и тех же пациентов) до и после воздействия (лечение, профилактика, реабилитационные мероприятия), такие выборки называются зависимыми.

Дисперсионный анализ, в котором проверяется влияние одного фактора, называется однофакторным (одномерный анализ). При изучении влияния более чем одного фактора используют многофакторный дисперсионный анализ (многомерный анализ).

Факторные признаки – это те признаки, которые влияют на изучаемое явление.

Результативные признаки – это те признаки, которые изменяются под влиянием факторных признаков.

Для проведения дисперсионного анализа могут использоваться как качественные (пол, профессия), так и количественные признаки ( число инъекций, больных в палате, число койко-дней).

Методыдисперсионного анализа:

1. Метод по Фишеру (Fisher) - критерий F;

2. Метод « общей линейной модели».

Первый метод применяется в однофакторном дисперсионном анализе, когда совокупная дисперсия всех наблюдаемых значений раскладывается на дисперсию внутри отдельных групп и дисперсию между группами.

В основе «обобщенной линейной модели» лежит корреляционный или регрессионный анализ, применяемый в многофакторном анализе.

Обычно в медико-биологических исследованиях используются только однофакторные, максимум двухфакторные дисперсионные комплексы. Многофакторные комплексы можно исследовать, последовательно анализируя одно- или двухфакторные комплексы, выделяемые из всей наблюдаемой совокупности.

Условия применения дисперсионного анализа:

1. Задачей исследования является определение силы влияния одного (до 3-х) факторов на результат или определение силы совместного влияния различных факторов (пол и возраст, физическая активность и питание и т.д.).

2. Изучаемые факторы должны быть независимые (несвязанные) между собой. Например, нельзя изучать совместное влияние стажа работы и возраста, роста и веса детей и т. д. а заболеваемость населения.

3. Подбор групп для исследования проводится рандомизированно (случайный отбор). Организация дисперсионного комплекса с выполнением принципа случайности отбора вариантов называется рандомизацией (перев. с англ.-random), т.е. выбранные наугад.

4. Можно применять как количественные, так и качественные (атрибутивные) признаки.

При проведении однофакторного дисперсионного анализа рекомендуется (необходимое условие применения):

1. Нормальность распределения анализируемых групп или соответствие выборочных групп генеральным совокупностям с нормальным распределением.

2. Независимость (не связанность) распределения наблюдений в группах.

3. Наличие частоты (повторность) наблюдений.

Нормальность распределения определяется кривой Гаусса (Де Мавура), которую можно описать функцией y = ƒ(х), так как относится к числу законов распределения, используемых для приближенного описания явлений, которые носят случайный, вероятностный характер. Предмет медико-биологических исследований – явления вероятностного характера, нормальное распределение в таких исследованиях встречается весьма часто.

Принцип применения метода дисперсионного анализа:

Сначала формулируется нулевая гипотеза, то есть предполагается, что исследуемые факторы не оказывают никакого влияния на значения результативного признака и полученные различия случайны.

Затем мы определяем, какова вероятность получить наблюдаемые (или более сильные) различия при условии справедливости нулевой гипотезы.

Если эта вероятность мала*, то мы отвергаем нулевую гипотезу и заключаем, что результаты исследования статистически значимы. Это еще не означает, что доказано действие именно изучаемых факторов (это вопрос, прежде всего,

планирования исследования), но все же маловероятно, что результат обусловлен случайностью.

При выполнении всех условий применения дисперсионного анализа, разложение общей дисперсии математически выглядит следующим образом:

D общ. = Dфакт.+ Dост.,где

Dобщ – общая дисперсия, наблюдаемых значений (вариант), характеризуется разбросом вариант от общего среднего. Измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию.Общее разнообразиескладывается из межгруппового и внутригруппового;

Dфакт.- факторная (межгрупповая) дисперсия, характеризуется различием средних в каждой группе и зависит от влияния исследуемого фактора, по которому дифференцируется каждая группа. Например, в группах различных по этиологическому фактору клинического течения пневмонии средний уровень проведенного койко-дня неодинаков – наблюдается межгрупповое разнообразие.

Dост.- остаточная ( внутригрупповая) дисперсия, которая характеризует рассеяние вариант внутри групп. Отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неутонченных факторов и не зависящую от признака – фактора, положенного в основание группировки. Вариация изучаемого признака зависит от силы влияния каких-то неучтенных случайных факторов, как от организованных (заданных исследователем),так и от случайных ( неизвестных) факторов.

Поэтому общая вариация (дисперсия) слагается из вариации, вызванной организованными (заданными) факторами, называемые факториальной вариацией и неорганизованными факторами, т.е. остаточнойвариацией ( случайной, неизвестной).

* Максимальную приемлемую вероятность отвергнуть верную нулевую гипотезу называют уровнем значимости и обозначают α = 0,05

Классический дисперсионный анализ проводится по следующим этапам:

1. Построение дисперсионного комплекса;

2. Вычисление средних квадратов отклонений;

3. Вычисление дисперсий;

4. Сравнение факторной и остаточной дисперсий;

5. Оценка результатов с помощью теоретических значений распределения Фишера-Снедекора.

Предлагаем упрощенный вариант классической формулы дисперсии