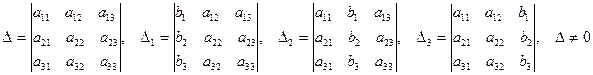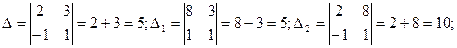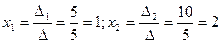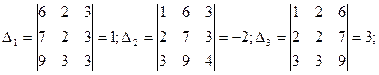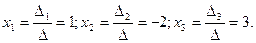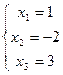Обратная связь
|
Решение систем линейных алгебраических уравнений Определители
Вычисление определителей второго и третьего порядка
Квадратной матрице А  порядка n можно поставить в соответствие число, обозначаемое det А (или порядка n можно поставить в соответствие число, обозначаемое det А (или  или или  ), называемое ее определителем (детерминантом), и вычисляемое по следующим схемам: ), называемое ее определителем (детерминантом), и вычисляемое по следующим схемам:
1.  det А det А  = = 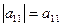
2. det А  = =  = += = += 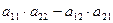
3. detА 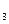 = =  = =  = = = = 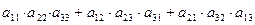 - - 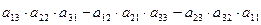
Пример: Вычислить определители матриц А=  , В= , В= 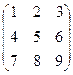
Решение: Det А= 
Det В= 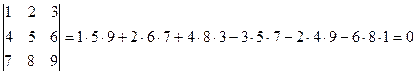
Ответ: detA=14, detB=0.
Разложение определителя матрицы по элементам строки или столбца
Опр: Минором  элемента элемента  определителя n-го порядка называется определитель (n-1)-го порядка ,полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится элемент определителя n-го порядка называется определитель (n-1)-го порядка ,полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится элемент  . .
Опр: Алгебраическим дополнением  элемента элемента  называется его минор, умноженный на число (-1) называется его минор, умноженный на число (-1)  : : 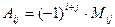
Теорема: Определитель матрицы равен сумме произведений элементов любой его строки (столбца) на их алгебраические дополнения.
Разложение определителя по любой (i-й, где i=1,2,…n) строке:
det 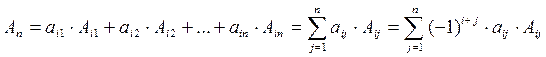
Разложение определителя по любому (j-му, где j=1,2,…n) столбцу:
detA  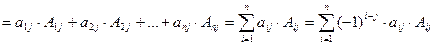
Пример: Найти минор  и алгебраическое дополнение и алгебраическое дополнение  элемента элемента  матрицы А= матрицы А=  . .
Решение:
  Найдем минор: М Найдем минор: М  = =  =0+0+2-15-8-0=-21; =0+0+2-15-8-0=-21;
Найдем алгебраическое дополнение: 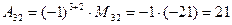
Ответ:  , , 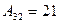
Пример: Вычислить определитель матрицы А=  . .
Решение: Вычислим определитель разложением по третьему столбцу:
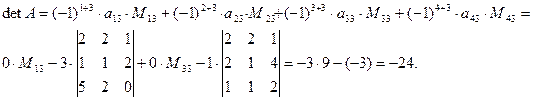
Ответ: detA=-24
Свойства определителя:
1. Определитель матрицы равен определителю транспонированной матрицы. det A=detA  . .
2. При перестановке местами двух параллельных строк или столбцов определитель меняет свой знак на противоположный.
3. Определитель, имеющий две одинаковые , или две пропорциональные строки или столбца равен нулю.
4. Общий множитель всех элементов строки или столбца можно выносить за знак определителя, т.е. 
5. Определитель, имеющий нулевую строку или столбец равен нулю.
6. Определитель не изменится, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на любое число. Это утверждение верно и для столбцов.
Обратная матрица
Опр: Квадратная матрица А называется невырожденной, если ее определитель не равен нулю, т.е. det A 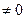
Опр: Матрицей, обратной к матрице А называется такая матрица  , которая удовлетворяет условиям: , которая удовлетворяет условиям:  . .
Все матрицы: А,  и Е имеют один и тот же порядок. и Е имеют один и тот же порядок.
Всякая невырожденная матрица имеет обратную, которая может быть найдена по формуле:  , где , где  алгебраическое дополнение элемента алгебраическое дополнение элемента  . Распишем последовательность нахождения обратной матрицы: . Распишем последовательность нахождения обратной матрицы:
Правило вычисления обратной матрицы:
1. Вычислить определитель матрицы detA ( detA 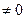 ,в противном случае обратная не существует.) ,в противном случае обратная не существует.)
2. Составить матрицу из алгебраических дополнений элементов:  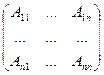
3. Каждый элемент полученной матрицы разделить на определитель:   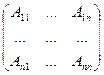
4. Транспонировать полученную матрицу: 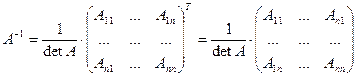
5. Результат проверить, умножив А на  . .
Пример: Для матрицы А=  найти обратную. найти обратную.
Решение:
1. Находим detA= 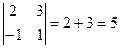
2. Составляем матрицу  , поэтому , поэтому 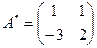
3. Делим элементы на определитель: 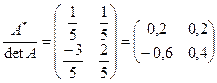
4. Транспонируем полученную матрицу: 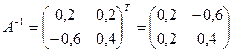
5. Проверка: 
Ответ: 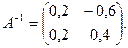
Пример: Для матрицы А=  найти обратную. найти обратную.
Решение:
Находим detA= 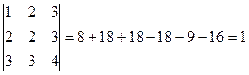
Составляем матрицу
   поэтому поэтому 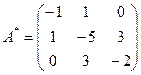
Делим элементы на определитель: 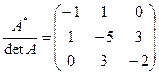
Транспонируем полученную матрицу: 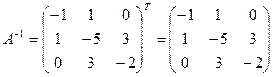
Проверка: 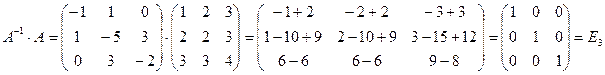
Ответ: 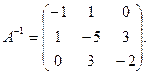
Решение систем линейных алгебраических уравнений
Рассмотрим систему m линейных алгебраических уравнений (СЛАУ) относительно n неизвестных 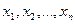 : : 
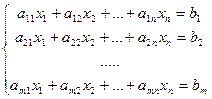 В соответствии с правилом умножения матриц, рассмотренная система линейных уравнений может быть записана в матричной форме AХ=В, где
В соответствии с правилом умножения матриц, рассмотренная система линейных уравнений может быть записана в матричной форме AХ=В, где
 , ,
 .
Матрица A, столбцами которой являются коэффициенты при соответствующих неизвестных, а строками - коэффициенты при неизвестных в соответствующем уравнении называется матрицей системы. Матрица-столбец B, элементами которой являются правые части уравнений системы, называется столбцом свободных переменных, или просто правой частью системы. Матрица-столбец X, элементами которой являются искомые неизвестные, называется столбцом переменных.
Система линейных алгебраических уравнений, записанная в виде AX=B, является матричным уравнением.
Пример 1: Записать систему в виде матричного уравнения: .
Матрица A, столбцами которой являются коэффициенты при соответствующих неизвестных, а строками - коэффициенты при неизвестных в соответствующем уравнении называется матрицей системы. Матрица-столбец B, элементами которой являются правые части уравнений системы, называется столбцом свободных переменных, или просто правой частью системы. Матрица-столбец X, элементами которой являются искомые неизвестные, называется столбцом переменных.
Система линейных алгебраических уравнений, записанная в виде AX=B, является матричным уравнением.
Пример 1: Записать систему в виде матричного уравнения: 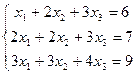 Решение: Матрица системы:
Решение: Матрица системы:  ,
столбец переменных: X= ,
столбец переменных: X=  ,
столбец свободных переменных : b= ,
столбец свободных переменных : b= 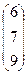 Ответ: Матричное уравнение имеет вид:
Ответ: Матричное уравнение имеет вид:
 Решением системы называется совокупность n значений неизвестных
Решением системы называется совокупность n значений неизвестных
 ,
при подстановке которых в систему, все уравнения обращаются в верные тождества. Или решение можно записать в виде столбца ,
при подстановке которых в систему, все уравнения обращаются в верные тождества. Или решение можно записать в виде столбца  , подстановка которого в матричное уравнение AX=B, обращает его в верное тождество.
Система, имеющая хотя бы одно решение, называется совместной; система, не имеющая ни одного решения — несовместной.
Если система имеет единственное решение, то система называется определенной, если решений много, то система называется неопределенной.
Решение матричных уравнений
Рассмотрим системы, число уравнений которых m равно числу переменных n и матрица системы А является невырожденной, т.е. detА , подстановка которого в матричное уравнение AX=B, обращает его в верное тождество.
Система, имеющая хотя бы одно решение, называется совместной; система, не имеющая ни одного решения — несовместной.
Если система имеет единственное решение, то система называется определенной, если решений много, то система называется неопределенной.
Решение матричных уравнений
Рассмотрим системы, число уравнений которых m равно числу переменных n и матрица системы А является невырожденной, т.е. detА 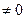 .Если матрица системы невырождена, то у нее существует обратная матрица А .Если матрица системы невырождена, то у нее существует обратная матрица А  . И тогда для решения матричного уравнения AX=B, необходимо обе части этого уравнения слева умножить на А . И тогда для решения матричного уравнения AX=B, необходимо обе части этого уравнения слева умножить на А  Получаем решение системы в виде: Получаем решение системы в виде:  .
Пример 2: Решить систему, как матричное уравнение: .
Пример 2: Решить систему, как матричное уравнение:  .
Решение:
1. Запишем систему в матричном виде: .
Решение:
1. Запишем систему в матричном виде:  .
2. Для матрицы системы .
2. Для матрицы системы 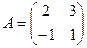 найдем обратную матрицу: найдем обратную матрицу:  ,
3. Решение системы ищем в виде: ,
3. Решение системы ищем в виде:  .
Ответ: .
Ответ:  .
Пример 3: Решить матричное уравнение: .
Пример 3: Решить матричное уравнение:
 .
Решение: Для матрицы системы А найдем обратную матрицу: .
Решение: Для матрицы системы А найдем обратную матрицу:
  1. Решение системы ищем в виде:
1. Решение системы ищем в виде:  . .  .
Ответ: .
Ответ:  .
Правило Крамера
Справедливо следующее утверждение (формулы Крамера): .
Правило Крамера
Справедливо следующее утверждение (формулы Крамера):
Если определитель  =det A матрицы системы Ax=В отличен от нуля, то система имеет единственное решение =det A матрицы системы Ax=В отличен от нуля, то система имеет единственное решение  определяемое формулами Крамера: определяемое формулами Крамера:  , где i=1,2, ., n, , где i=1,2, ., n,
| где  - определитель матрицы n -го порядка, полученной из матрицы A системы заменой i -го столбца столбцом свободных переменных b. - определитель матрицы n -го порядка, полученной из матрицы A системы заменой i -го столбца столбцом свободных переменных b.
Применим правило Крамера для решения системы двух линейных уравнений с двумя неизвестными.
Рассмотрим систему:  , ,
где
 - главный определитель; - главный определитель;
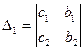 , ,  - вспомогательные определители. Они получаются заменой в главном определителе колонки коэффициентов при х (D1) и при y (D2) колонкой свободных членов. - вспомогательные определители. Они получаются заменой в главном определителе колонки коэффициентов при х (D1) и при y (D2) колонкой свободных членов.
Решение системы по правилу Крамера имеет вид:
 . .
Для систем трех уравнений с тремя неизвестными
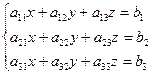
правило Крамера имеет вид:
 , ,
где 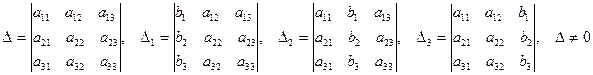
Пример 4. Решить систему по формулам Крамера:  . .
Решение: 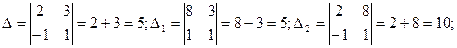
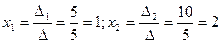
Ответ: 
Пример 5: Решить систему по формулам Крамера: 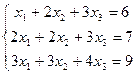
Решение:  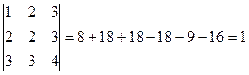
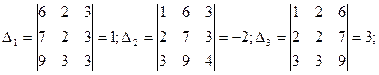
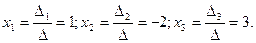
Ответ: 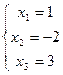
|
|
©2015- 2025 pdnr.ru Все права принадлежат авторам размещенных материалов.
|
|
 порядка n можно поставить в соответствие число, обозначаемое det А (или
порядка n можно поставить в соответствие число, обозначаемое det А (или  или
или  ), называемое ее определителем (детерминантом), и вычисляемое по следующим схемам:
), называемое ее определителем (детерминантом), и вычисляемое по следующим схемам: det А
det А  =
= 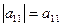
 =
=  = +=
= += 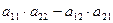
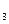 =
=  =
=  = =
= = 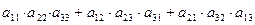 -
- 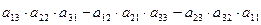
 , В=
, В= 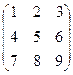

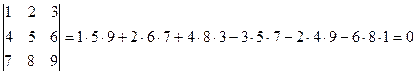
 элемента
элемента  определителя n-го порядка называется определитель (n-1)-го порядка ,полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится элемент
определителя n-го порядка называется определитель (n-1)-го порядка ,полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится элемент  элемента
элемента  :
: 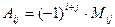
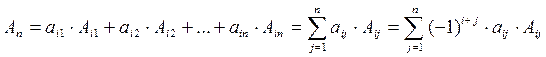
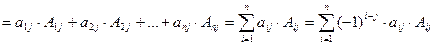
 и алгебраическое дополнение
и алгебраическое дополнение  элемента
элемента  матрицы А=
матрицы А=  .
.
 =
=  =0+0+2-15-8-0=-21;
=0+0+2-15-8-0=-21;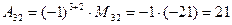
 ,
, 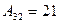
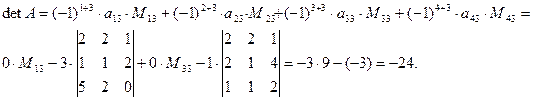
 .
.
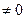
 , которая удовлетворяет условиям:
, которая удовлетворяет условиям:  .
. , где
, где  алгебраическое дополнение элемента
алгебраическое дополнение элемента 
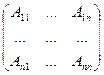


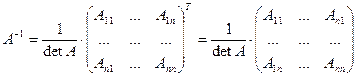
 .
. найти обратную.
найти обратную.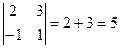
 , поэтому
, поэтому 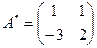
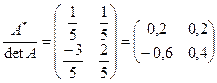
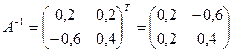

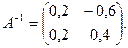
 найти обратную.
найти обратную.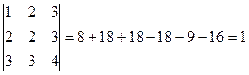


 поэтому
поэтому 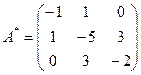
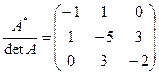
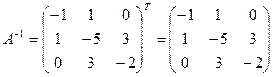
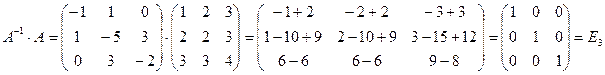
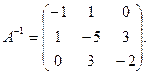
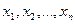 :
: 
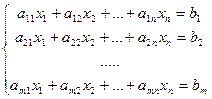 В соответствии с правилом умножения матриц, рассмотренная система линейных уравнений может быть записана в матричной форме AХ=В, где
В соответствии с правилом умножения матриц, рассмотренная система линейных уравнений может быть записана в матричной форме AХ=В, где
 ,
,
 .
Матрица A, столбцами которой являются коэффициенты при соответствующих неизвестных, а строками - коэффициенты при неизвестных в соответствующем уравнении называется матрицей системы. Матрица-столбец B, элементами которой являются правые части уравнений системы, называется столбцом свободных переменных, или просто правой частью системы. Матрица-столбец X, элементами которой являются искомые неизвестные, называется столбцом переменных.
Система линейных алгебраических уравнений, записанная в виде AX=B, является матричным уравнением.
Пример 1: Записать систему в виде матричного уравнения:
.
Матрица A, столбцами которой являются коэффициенты при соответствующих неизвестных, а строками - коэффициенты при неизвестных в соответствующем уравнении называется матрицей системы. Матрица-столбец B, элементами которой являются правые части уравнений системы, называется столбцом свободных переменных, или просто правой частью системы. Матрица-столбец X, элементами которой являются искомые неизвестные, называется столбцом переменных.
Система линейных алгебраических уравнений, записанная в виде AX=B, является матричным уравнением.
Пример 1: Записать систему в виде матричного уравнения: 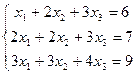 Решение: Матрица системы:
Решение: Матрица системы:  ,
столбец переменных: X=
,
столбец переменных: X=  ,
столбец свободных переменных : b=
,
столбец свободных переменных : b= 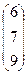 Ответ: Матричное уравнение имеет вид:
Ответ: Матричное уравнение имеет вид:
 Решением системы называется совокупность n значений неизвестных
Решением системы называется совокупность n значений неизвестных
 ,
при подстановке которых в систему, все уравнения обращаются в верные тождества. Или решение можно записать в виде столбца
,
при подстановке которых в систему, все уравнения обращаются в верные тождества. Или решение можно записать в виде столбца  , подстановка которого в матричное уравнение AX=B, обращает его в верное тождество.
Система, имеющая хотя бы одно решение, называется совместной; система, не имеющая ни одного решения — несовместной.
Если система имеет единственное решение, то система называется определенной, если решений много, то система называется неопределенной.
Решение матричных уравнений
Рассмотрим системы, число уравнений которых m равно числу переменных n и матрица системы А является невырожденной, т.е. detА
, подстановка которого в матричное уравнение AX=B, обращает его в верное тождество.
Система, имеющая хотя бы одно решение, называется совместной; система, не имеющая ни одного решения — несовместной.
Если система имеет единственное решение, то система называется определенной, если решений много, то система называется неопределенной.
Решение матричных уравнений
Рассмотрим системы, число уравнений которых m равно числу переменных n и матрица системы А является невырожденной, т.е. detА  . И тогда для решения матричного уравнения AX=B, необходимо обе части этого уравнения слева умножить на А
. И тогда для решения матричного уравнения AX=B, необходимо обе части этого уравнения слева умножить на А  .
Пример 2: Решить систему, как матричное уравнение:
.
Пример 2: Решить систему, как матричное уравнение:  .
Решение:
1. Запишем систему в матричном виде:
.
Решение:
1. Запишем систему в матричном виде:  .
2. Для матрицы системы
.
2. Для матрицы системы 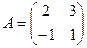 найдем обратную матрицу:
найдем обратную матрицу:  ,
3. Решение системы ищем в виде:
,
3. Решение системы ищем в виде:  .
Ответ:
.
Ответ:  .
Пример 3: Решить матричное уравнение:
.
Пример 3: Решить матричное уравнение:
 1. Решение системы ищем в виде:
1. Решение системы ищем в виде:  .
.  .
Ответ:
.
Ответ:  .
Правило Крамера
Справедливо следующее утверждение (формулы Крамера):
.
Правило Крамера
Справедливо следующее утверждение (формулы Крамера):
 определяемое формулами Крамера:
определяемое формулами Крамера:  , где i=1,2, ., n,
, где i=1,2, ., n,
 - определитель матрицы n -го порядка, полученной из матрицы A системы заменой i -го столбца столбцом свободных переменных b.
- определитель матрицы n -го порядка, полученной из матрицы A системы заменой i -го столбца столбцом свободных переменных b. ,
, - главный определитель;
- главный определитель;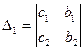 ,
,  - вспомогательные определители. Они получаются заменой в главном определителе колонки коэффициентов при х (D1) и при y (D2) колонкой свободных членов.
- вспомогательные определители. Они получаются заменой в главном определителе колонки коэффициентов при х (D1) и при y (D2) колонкой свободных членов. .
.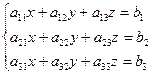
 ,
,