Пиши Дома Нужные Работы
Обратная связь
|
Метод Гаусса решения систем линейных уравнений Метод Гаусса является одним из наиболее универсальных и эффективных методов решения систем линейных алгебраических уравнений. Он применим как для решения системы линейных алгебраических уравнений с невырожденной матрицей, так и для систем с вырожденной матрицей и для систем, число уравнений которых не совпадает с числом переменных. Идея метода Гаусса состоит в том, что систему m линейных алгебраических уравнений относительно n неизвестных  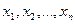 : :
 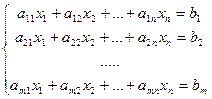
приводят с помощью эквивалентных преобразований, не меняющих решения системы, к ступенчатому виду( в частности, к верхнетреугольному)
  , ,
решение которой находят следующим образом: выражают 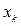 .из последнего уравнения, подставляют в предпоследнее, из которого выражается .из последнего уравнения, подставляют в предпоследнее, из которого выражается 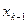 и т.д., из первого уравнения выражается и т.д., из первого уравнения выражается 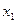 . .
Матричная запись метода Гаусса
1.Прямой ход метода Гаусса: выписывается расширенная матрица системы( справа к матрице системы приписывается столбец свободных переменных)
 , ,
применяем элементарные преобразования над строками для приведения матрицы к ступенчатому виду:
· строки можно переставлят местами;
· строку можно умножать на любое число, не равное нулю;
· к строке можно поэлементно прибавлять другую строку, умноженную на ненулевое число.
1-й этап:
Считая элемент 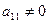 ( в противном случае переставляем местами строки), обнулим все элементы первого столбца кроме ( в противном случае переставляем местами строки), обнулим все элементы первого столбца кроме 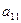 . .
Для этого ко второй строке прибавим первую строку, умноженную на  . .
К третьей строке прибавим вторую, умноженную на 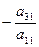 и т.д. и т.д.
Получим преобразованную матрицу:
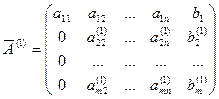 , где , где  и и 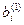 - преобразованные коэффициенты матрицы. - преобразованные коэффициенты матрицы.
2-й этап:
Считая 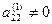 , обнулим все коэффициенты второго столбца, кроме , обнулим все коэффициенты второго столбца, кроме 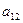 и и 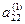 , для чего к каждой строке прибавляем вторую строку, умноженную на соответствующий коэффициент. , для чего к каждой строке прибавляем вторую строку, умноженную на соответствующий коэффициент.
Если в процессе приведения появляется нулевая строка, ее выбрасываем. Если появляется строка, все коэффициенты которой нули, а последний 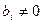 , то система несовместна. , то система несовместна.
Обратный ход метода Гаусса: По виду ступенчатой матрицы: 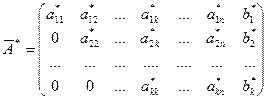 восстановить систему: восстановить систему: 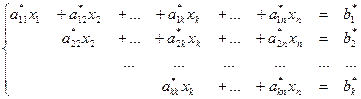 , ,
Если число оставшихся уравнений и число переменных совпадает, то система имеет единственное решение. Если же переменных больше, чем уравнений, то переменные, вышедшие на диагональ называются главными, или зависимыми, а переменные не вышедшие на диагональ свободными. Свободные переменные необходимо перенести в правую часть уравнения и начиная с последнего уравнения выразить главную переменную  ,подставить в предпоследнее, из которого выразить ,подставить в предпоследнее, из которого выразить 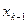 , и т.д., из первого уравнения выразить , и т.д., из первого уравнения выразить 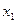 . В этом случае система имеет множество решений. Свободные переменные могут приобретать любые значения, и через них выражаются значения зависимых переменных. . В этом случае система имеет множество решений. Свободные переменные могут приобретать любые значения, и через них выражаются значения зависимых переменных.
Пример 6: Решить систему методом Гаусса:
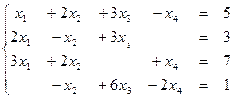
Решение: Выпишем расширенную матрицу системы и приведем ее к верхнетреугольному виду:
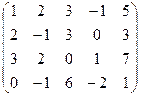  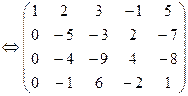 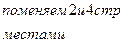 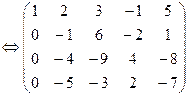 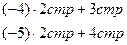 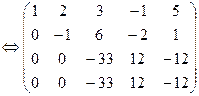 
|
|
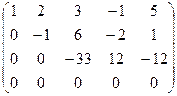
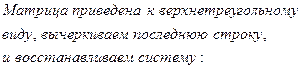
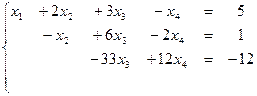
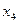 является свободной переменной, т.к. не вышла на диагональ, переносим ее вправо. Система имеет бесконечное множество решений.
является свободной переменной, т.к. не вышла на диагональ, переносим ее вправо. Система имеет бесконечное множество решений.
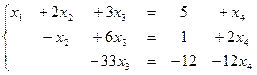
Из последнего уравнения выражаем 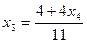
Из второго уравнения выражаем 
Из первого уравнения выражаем 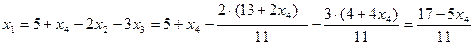
Выпишем общее решение системы: 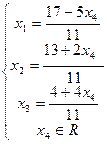
Ответ: Система имеет множество решений, общее решение системы:
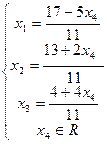
Решение однородных систем
Система линейных уравнений называется однородной, если правые части уравнений равны нулю:
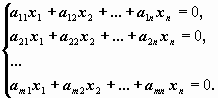
Матричный вид однородной системы: Ax=0.
Однородная система всегда совместна, поскольку любая однородная линейная система имеет по крайней мере одно решение:
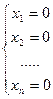
Если однородная система имеет единственное решение, то это единственное решение — нулевое, и система называется тривиально совместной. Если же однородная система имеет более одного решения, то среди них есть и ненулевые и в этом случае система называется нетривиально совместной.
Доказано, что при m=n для нетривиальной совместности системы необходимо и достаточно, чтобы определитель матрицы системы был равен нулю. Линейная комбинация решений однородной системы также является решением этой системы.
Пример: Исследовать однородную систему на совместность, найти решения: 
Решение: Расширенную матрицу системы приведем к ступенчатому виду: 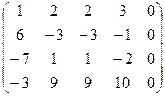
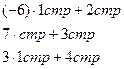
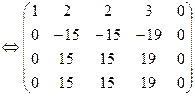


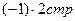
 восстановим систему:
восстановим систему:
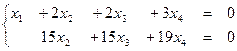
Система имеет множество решений. 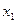 и
и 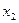 главные переменные,
главные переменные, 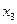 и
и 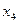 свободные переменные. Перенесем свободные переменные в правые части уравнений.
свободные переменные. Перенесем свободные переменные в правые части уравнений.
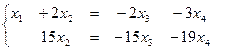
Из второго уравнения находим  подставляя это выражение в первое уравнение, получим:
подставляя это выражение в первое уравнение, получим: 
Общее решение системы:
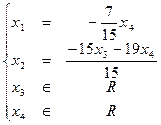
Для нахождения частных решений, свободным переменным даем произвольные значения: 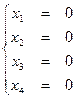

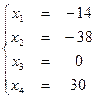
Элементы векторной алгебры
Векторы
Величины, которые полностью определяются своим численным значением, называются скалярными. Другие величины, например сила, скорость, ускорение, определяются не только своим числовым значением, но и направлением. Такие величины называют векторными.
Вектор-это направленный прямолинейный отрезок, т. е. отрезок, имеющий определенную длину и определенное направление. Если А- начало вектора, а В- его конец, то вектор обозначается символом  , или
, или 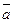 . Вектор
. Вектор 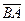 ( у него начало в точке В , а конец в точке А) называется противоположным вектору
( у него начало в точке В , а конец в точке А) называется противоположным вектору  . Вектор, противоположный вектору
. Вектор, противоположный вектору 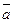 , обозначается
, обозначается 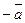 .
.
Длиной или модулем вектора  называется длина отрезка AB и обозначается
называется длина отрезка AB и обозначается 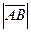 . Вектор, длина которого равна нулю, называется нулевым вектором и обозначается
. Вектор, длина которого равна нулю, называется нулевым вектором и обозначается  . Нулевой вектор направления не имеет. Вектор единичной длины, направление которого совпадает с направлением вектора
. Нулевой вектор направления не имеет. Вектор единичной длины, направление которого совпадает с направлением вектора 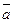 , называется ортом вектора
, называется ортом вектора 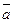 и обозначается
и обозначается 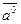 .
.
Векторы 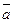
 и
и 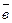 называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Обозначаются коллинеарные векторы
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Обозначаются коллинеарные векторы 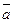 ║
║ 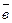

Коллинеарные векторы могут быть направлены одинаково, т.е. быть сонаправленными ( 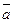

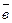 ), или быть противоположно направленными (
), или быть противоположно направленными ( 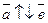 ).
).
Нулевой вектор считается коллинеарным любому вектору.
Два вектора 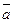 и
и 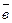 называются равными (
называются равными ( 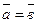 ), если они коллинеарные, одинаково направлены и имеют одинаковые длины.
), если они коллинеарные, одинаково направлены и имеют одинаковые длины.
Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора перемешать в любую точку пространства.
Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или хотя бы два коллинеарные, то такие векторы будут компланарны.
|
©2015- 2025 pdnr.ru Все права принадлежат авторам размещенных материалов.

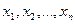 :
:
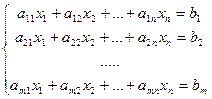
 ,
,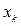 .из последнего уравнения, подставляют в предпоследнее, из которого выражается
.из последнего уравнения, подставляют в предпоследнее, из которого выражается 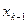 и т.д., из первого уравнения выражается
и т.д., из первого уравнения выражается 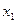 .
. ,
,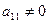 ( в противном случае переставляем местами строки), обнулим все элементы первого столбца кроме
( в противном случае переставляем местами строки), обнулим все элементы первого столбца кроме 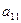 .
. .
.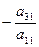 и т.д.
и т.д.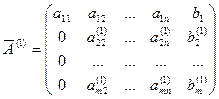 , где
, где  и
и 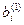 - преобразованные коэффициенты матрицы.
- преобразованные коэффициенты матрицы.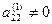 , обнулим все коэффициенты второго столбца, кроме
, обнулим все коэффициенты второго столбца, кроме 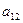 и
и 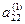 , для чего к каждой строке прибавляем вторую строку, умноженную на соответствующий коэффициент.
, для чего к каждой строке прибавляем вторую строку, умноженную на соответствующий коэффициент.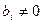 , то система несовместна.
, то система несовместна.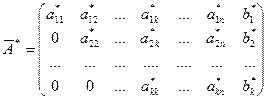 восстановить систему:
восстановить систему: 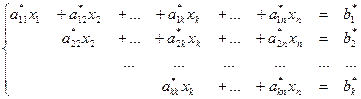 ,
, ,подставить в предпоследнее, из которого выразить
,подставить в предпоследнее, из которого выразить 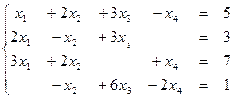
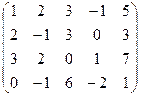

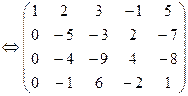
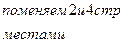
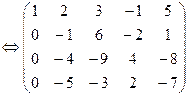
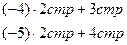
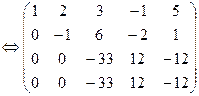

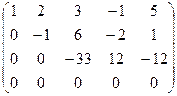
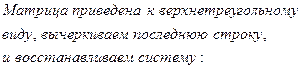
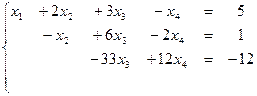
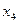 является свободной переменной, т.к. не вышла на диагональ, переносим ее вправо. Система имеет бесконечное множество решений.
является свободной переменной, т.к. не вышла на диагональ, переносим ее вправо. Система имеет бесконечное множество решений.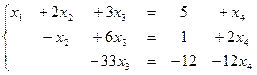
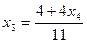

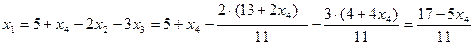
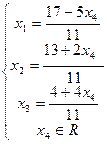
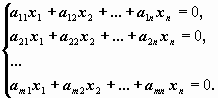
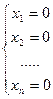

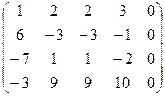
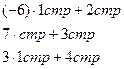
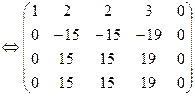


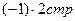
 восстановим систему:
восстановим систему: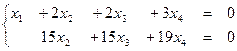
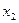 главные переменные,
главные переменные, 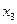 и
и 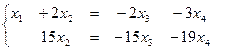
 подставляя это выражение в первое уравнение, получим:
подставляя это выражение в первое уравнение, получим: 
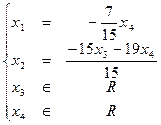
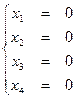

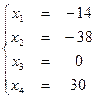
 , или
, или 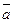 . Вектор
. Вектор 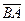 ( у него начало в точке В , а конец в точке А) называется противоположным вектору
( у него начало в точке В , а конец в точке А) называется противоположным вектору 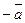 .
.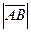 . Вектор, длина которого равна нулю, называется нулевым вектором и обозначается
. Вектор, длина которого равна нулю, называется нулевым вектором и обозначается  . Нулевой вектор направления не имеет. Вектор единичной длины, направление которого совпадает с направлением вектора
. Нулевой вектор направления не имеет. Вектор единичной длины, направление которого совпадает с направлением вектора 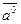 .
.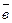 называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Обозначаются коллинеарные векторы
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Обозначаются коллинеарные векторы 
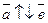 ).
).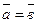 ), если они коллинеарные, одинаково направлены и имеют одинаковые длины.
), если они коллинеарные, одинаково направлены и имеют одинаковые длины.