|
|
Прямая, проходящая через точку, параллельно данному векторуОпр: Направляющим вектором прямой называется вектор, параллельный данной прямой. Составим уравнение прямой
Данная форма записи уравнения прямой называется каноническое уравнение прямой. Для того, чтобы преобразовать каноническое уравнение в общий вид, необходимо разрешить пропорцию: Прямую, заданную в каноническом виде можно представить в параметрическом виде, для этого введем параметр p, и каждое отношение приравняем к параметру t. Решим полученные уравнения относительно x и y :
Получено параметрическое уравнение прямой линии на плоскости.
Уравнение прямой, проходящей через две точки
В качестве направляющего вектора прямой можно взять вектор
Уравнение прямой в отрезках
Подставим координаты этих точек в уравнение прямой, проходящей через две точки,
Это уравнение называется уравнением прямой в отрезках, так как числа a и b указывают, какие отрезки отсекает прямая на осях координат.
Уравнение прямой с угловым коэффициентом Опр: Угловым коэффициентом прямой называется тангенс угла между прямой и положительным направлением оси ОХ. Обозначается угловой коэффициент: k=tg b- отрезок, который прямая отсекает на оси ОУ уравнение
Если прямая проходит через начало координат, то b= 0 и, следовательно, уравнение этой прямой будет иметь вид у = кх.
Если прямая параллельна оси Ох, то
Если прямая параллельна оси Оу, то уравнение имеет вид: х = а где а — абсцисса точки пересечения прямой с осью Ох. Прямая, проходящая через точку, в данном направлении
Уравнение
Угол между прямыми При пересечении двух прямых образуются четыре угла:, тангенс и косинус которых отличаются знаком. Приведены формулы для вычисления острого угла между прямыми. Если две прямые заданы своими общими уравнениеми:
Условие перпендикулярности: Условие параллельности: Если две прямые заданы уравнениями с угловыми коэффициентами:
Точка пересечения прямых Пусть две прямые заданы своими общими уравнениями:
Чтобы найти общую точку, необходимо решить систему двух уравнений с двумя переменными.
Расстояние от точки до прямой Пусть заданы координаты точки
Проекция точки на прямую Пусть необходимо спроектировать точку
Пример: Даны вершины треугольника 1) уравнение высоты, опущенной из вершины 2) точку пересечения высоты 3) точку пересечения медиан треугольника Решение: 1) Составим уравнение высоты
Ответ: 2) Составим уравнение стороны
Найдем точку пересечения высоты
Ответ: N 3) Найдем середину стороны
Составим уравнение прямой проходящей через точку
Найдем середину стороны
Составим уравнение прямой проходящей через точку
Найдем точку О пересечения найденных медиан:
Ответ: О
Плоскость Общее уравнение плоскости Алгебраическое уравнение первой степени в пространстве определяет плоскость. Общее уравнение плоскости можно записать в виде: Ax+ By+ Cz+ D=0 Любую плоскость можно представить в виде такого уравнение единственным способом. с точностью до коэффициента (т. е. при умножении уравнения на число, полученное уравнение задает ту же плоскость ) Плоскость в пространстве можно задать различными способами, рассмотрим некоторые из них:
|
|
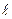 , проходящей через точку
, проходящей через точку  , параллельно вектору
, параллельно вектору  .
. Возьмем произвольную точку М(х,у), принадлежащую прямой, составим вектор
Возьмем произвольную точку М(х,у), принадлежащую прямой, составим вектор  . Векторы
. Векторы  должны быть коллинеарны, следовательно. Их координаты должны быть пропорциональны, т.е.
должны быть коллинеарны, следовательно. Их координаты должны быть пропорциональны, т.е.
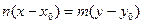 ;
; 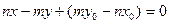
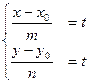 ;
; 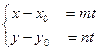 ;
; 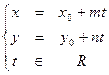
 Составим уравнение прямой, проходящей через две данные точки
Составим уравнение прямой, проходящей через две данные точки  и
и  .
. . Подставим координаты точки
. Подставим координаты точки 
 Пусть прямая пересекает ось Ох в точке
Пусть прямая пересекает ось Ох в точке 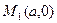 , а ось Оу - в точке
, а ось Оу - в точке  .
. После преобразований получим:
После преобразований получим:


 , где
, где 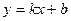 — уравнением прямой с угловым коэффициентом.
— уравнением прямой с угловым коэффициентом. Пусть прямая проходит через точку
Пусть прямая проходит через точку  и ее направление характеризуется конкретным угловым коэффициентом к. Уравнение этой прямой можно записать в виде:
и ее направление характеризуется конкретным угловым коэффициентом к. Уравнение этой прямой можно записать в виде: 
 , нормаль к прямой
, нормаль к прямой  :
: 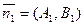
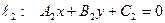 , нормаль к прямой
, нормаль к прямой  :
: 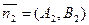
 Угол между прямыми есть угол между нормалями к прямым
Угол между прямыми есть угол между нормалями к прямым 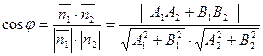
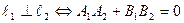
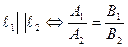

 ,
, то вычисляется тангенс угла между прямыми:
то вычисляется тангенс угла между прямыми:
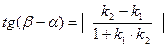

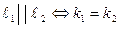
 , если система несовместна, то прямые параллельны.
, если система несовместна, то прямые параллельны.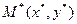 и уравнение прямой
и уравнение прямой  Расстояние от точки до прямой есть длина перпендикуляра, опущенного из точки на прямую:
Расстояние от точки до прямой есть длина перпендикуляра, опущенного из точки на прямую:
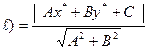
 Ах+Ву+С=0. проекцией точки на прямую является основание перпендикуляра, опущенного из точки на прямую. Нормалью к данной прямой является вектор
Ах+Ву+С=0. проекцией точки на прямую является основание перпендикуляра, опущенного из точки на прямую. Нормалью к данной прямой является вектор  . Составим уравнение проецирующей прямой. Она проходит через точку
. Составим уравнение проецирующей прямой. Она проходит через точку  . Подставив координаты точки и вектора в каноническое уравнение прямой
. Подставив координаты точки и вектора в каноническое уравнение прямой  . Теперь необходимо найти координаты точки пересечения данной прямой и проектирующей, для чего объединим их в систему:
. Теперь необходимо найти координаты точки пересечения данной прямой и проектирующей, для чего объединим их в систему: 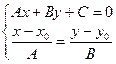 решение этой системы есть координаты точки, являющейся проекцией точки
решение этой системы есть координаты точки, являющейся проекцией точки  на прямую
на прямую  :
:  ;
;  ;
; 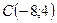 . Найти:
. Найти: ;
; и стороны
и стороны  ;
; :
: ;
;  ,
,  .
. ,
,  ,
,  ,
, .
.


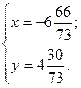
 .
. :
: ,
,  ,
,  ,
,  .
.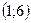 :
: ,
,  ,
,  ,
,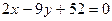 .
. :
: ,
,  .
. ,
,  .
. :
: ,
,  ,
,  ,
, .
.

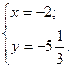
 .
.