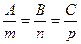Уравнение прямой, проходящей через две заданные точки Пусть необходимо составить уравнение прямой  , проходящей через две заданные точки: , проходящей через две заданные точки:  и и  . Вектор . Вектор  является направляющим вектором прямой. Составим уравнение прямой является направляющим вектором прямой. Составим уравнение прямой  по точке по точке  и направляющему вектору и направляющему вектору  : :
Уравнение прямой, проходящей через заданную точку, перпендикулярно данной плоскости
 Пусть необходимо составить уравнение прямой Пусть необходимо составить уравнение прямой  , проходящей через точку , проходящей через точку  , перпендикулярно плоскости , перпендикулярно плоскости 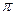 , заданной уравнением: Ах+Ву+Сz+D=0. Выпишем нормаль к плоскости, вектор , заданной уравнением: Ах+Ву+Сz+D=0. Выпишем нормаль к плоскости, вектор 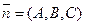 . Для искомой прямой этот вектор является направляющим вектором. Составим уравнение прямой . Для искомой прямой этот вектор является направляющим вектором. Составим уравнение прямой 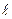 по точке по точке  и направляющему вектору и направляющему вектору  : :
Перевод уравнения прямой из канонического вида в параметрический
Пусть имеется уравнение прямой 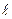 в каноническом виде: в каноническом виде:  . Для того, чтобы перевести уравнение в параметрический вид, введем параметр t и приравняем каждое отношение к параметру t. В результате получим: . Для того, чтобы перевести уравнение в параметрический вид, введем параметр t и приравняем каждое отношение к параметру t. В результате получим:   . .
Прямая 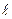 в параметрическом виде: в параметрическом виде: 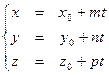 где где 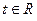
Перевод уравнения прямой из общего вида в канонический
Пусть прямая 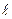 задана в общем виде: задана в общем виде: 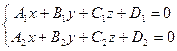 для того, чтобы перевести ее в канонический вид, возьмем две точки принадлежащие данной прямой, т.е. два частных решения данной системы. Для получения частного решения системы, проще всего одной из переменных дать произвольное значение, например, для того, чтобы перевести ее в канонический вид, возьмем две точки принадлежащие данной прямой, т.е. два частных решения данной системы. Для получения частного решения системы, проще всего одной из переменных дать произвольное значение, например,  . Подставить это значение в систему и решить полученную систему с двумя переменными: . Подставить это значение в систему и решить полученную систему с двумя переменными:  , например, по правилу Крамера: , например, по правилу Крамера:
 , ,  , найдена точка , найдена точка  . Если же определитель . Если же определитель  , то необходимо другой переменной дать произвольное значение, например, , то необходимо другой переменной дать произвольное значение, например,  и решить систему относительно х и z .Аналогично найти еще одно частное решение системы и решить систему относительно х и z .Аналогично найти еще одно частное решение системы  . И записать уравнение прямой по двум точкам: . И записать уравнение прямой по двум точкам:  . .
Перевод уравнения прямой из канонического вида в общий
Пусть дана прямая 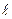 в каноническом виде: в каноническом виде:  . Для того, чтобы ее перевести в общий вид, приравняем попарно отношения ( при условии, что . Для того, чтобы ее перевести в общий вид, приравняем попарно отношения ( при условии, что  ): ):  после преобразований получим: после преобразований получим: 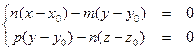
Прямая 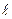 получена в общем виде, как пересечение двух плоскостей. Если же n=0. то можно получить одну из плоскостей, приравняв первое отношение к третьему. получена в общем виде, как пересечение двух плоскостей. Если же n=0. то можно получить одну из плоскостей, приравняв первое отношение к третьему.
Угол между прямыми в пространстве
Пусть две прямые  и и  заданы каноническими уравнениями: заданы каноническими уравнениями:
 : :  и и
  : :  . .
Выпишем направляющие векторы этих прямых:
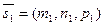 , ,  . Угол . Угол  между прямыми равен углу между их направляющими векторами: между прямыми равен углу между их направляющими векторами:  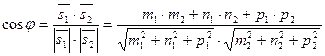 . Для нахождения острого угла между прямыми, числитель правой части следует взять по модулю. . Для нахождения острого угла между прямыми, числитель правой части следует взять по модулю.
· Условие параллельности прямых:  ││ ││   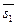 ││ ││  , или в координатной форме: , или в координатной форме:  . .
· Условие перпендикулярности прямых:     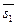   , а в координатной форме: , а в координатной форме:  . .
Взаимное расположение прямых в пространстве
Пусть две прямые в пространстве заданы каноническими уравнениями:
 : :  и и
  : :  их направляющие векторы соответственно: их направляющие векторы соответственно: 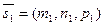 и и  . Точка . Точка  принадлежит прямой принадлежит прямой  , а точка , а точка  принадлежит принадлежит  .Составим вектор .Составим вектор  . По взаимному расположению векторов . По взаимному расположению векторов  можно судить о взаимном расположении прямых: можно судить о взаимном расположении прямых:
Прямые параллельны, если 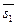 и и  коллинеарны и коллинеарны и
 не параллелен не параллелен 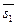
 Две прямые пересекаются в пространстве, если Две прямые пересекаются в пространстве, если 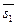 и и  не коллинеарны, а векторы не коллинеарны, а векторы  , ,  и и  компланарны., т.е. их смешанное произведение равно нулю: компланарны., т.е. их смешанное произведение равно нулю: 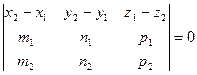
 Две прямые скрещиваются, если векторы Две прямые скрещиваются, если векторы  , ,  и и  не компланарны, т.е. их смешанное произведение не равно нулю. не компланарны, т.е. их смешанное произведение не равно нулю. 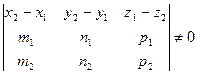
Угол между прямой и плоскостью
Пусть плоскость 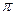 задана своим общим уравнением: Ax+By+Cz+D=0, а прямая задана своим общим уравнением: Ax+By+Cz+D=0, а прямая 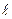 в каноническом виде: в каноническом виде:  . Углом между прямой и плоскостью называется угол между прямой и ее проекцией на плоскость. . Углом между прямой и плоскостью называется угол между прямой и ее проекцией на плоскость.
 Обозначим через Обозначим через  угол между прямой угол между прямой 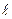 и плоскостью и плоскостью 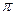 . Тогда угол между нормалью к плоскости вектором . Тогда угол между нормалью к плоскости вектором  и направляющим вектором прямой и направляющим вектором прямой  будет равен будет равен  . .
Тогда sin  =cos =cos  . Так как угол . Так как угол 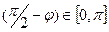 , то синус острого угла между прямой , то синус острого угла между прямой 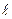 и плоскостью и плоскостью 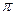 можно найти по формуле: можно найти по формуле: 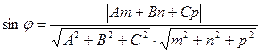
Условие параллельности прямой 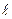 и плоскости и плоскости 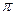
 Если прямая Если прямая 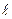 параллельна плоскости параллельна плоскости 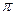 , то векторы , то векторы  и и  перпендикулярны, т.е. их скалярное произведение равно 0. перпендикулярны, т.е. их скалярное произведение равно 0.  , т.е. в координатной форме: Am+Bn+Cp=0. , т.е. в координатной форме: Am+Bn+Cp=0.
Условие перпендикулярности прямой 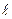 и плоскости и плоскости 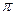
 Если прямая Если прямая 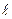 перпендикулярна плоскости перпендикулярна плоскости 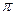 , то векторы , то векторы  и и  параллельны, т.е. должно быть выполнено равенство: параллельны, т.е. должно быть выполнено равенство: 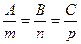
|
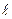 , проходящей через две заданные точки:
, проходящей через две заданные точки:  и
и  . Вектор
. Вектор  является направляющим вектором прямой. Составим уравнение прямой
является направляющим вектором прямой. Составим уравнение прямой  и направляющему вектору
и направляющему вектору  :
:
 Пусть необходимо составить уравнение прямой
Пусть необходимо составить уравнение прямой 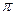 , заданной уравнением: Ах+Ву+Сz+D=0. Выпишем нормаль к плоскости, вектор
, заданной уравнением: Ах+Ву+Сz+D=0. Выпишем нормаль к плоскости, вектор 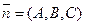 . Для искомой прямой этот вектор является направляющим вектором. Составим уравнение прямой
. Для искомой прямой этот вектор является направляющим вектором. Составим уравнение прямой  :
:
 . Для того, чтобы перевести уравнение в параметрический вид, введем параметр t и приравняем каждое отношение к параметру t. В результате получим:
. Для того, чтобы перевести уравнение в параметрический вид, введем параметр t и приравняем каждое отношение к параметру t. В результате получим: 
 .
.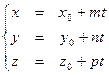 где
где 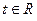
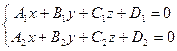 для того, чтобы перевести ее в канонический вид, возьмем две точки принадлежащие данной прямой, т.е. два частных решения данной системы. Для получения частного решения системы, проще всего одной из переменных дать произвольное значение, например,
для того, чтобы перевести ее в канонический вид, возьмем две точки принадлежащие данной прямой, т.е. два частных решения данной системы. Для получения частного решения системы, проще всего одной из переменных дать произвольное значение, например,  . Подставить это значение в систему и решить полученную систему с двумя переменными:
. Подставить это значение в систему и решить полученную систему с двумя переменными:  , например, по правилу Крамера:
, например, по правилу Крамера: ,
,  , найдена точка
, найдена точка  , то необходимо другой переменной дать произвольное значение, например,
, то необходимо другой переменной дать произвольное значение, например,  и решить систему относительно х и z .Аналогично найти еще одно частное решение системы
и решить систему относительно х и z .Аналогично найти еще одно частное решение системы  ):
):  после преобразований получим:
после преобразований получим: 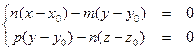
 и
и  заданы каноническими уравнениями:
заданы каноническими уравнениями: и
и
 .
.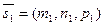 ,
,  . Угол
. Угол  между прямыми равен углу между их направляющими векторами:
между прямыми равен углу между их направляющими векторами: 
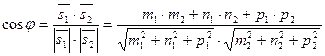 . Для нахождения острого угла между прямыми, числитель правой части следует взять по модулю.
. Для нахождения острого угла между прямыми, числитель правой части следует взять по модулю.
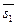 ││
││  , или в координатной форме:
, или в координатной форме:  .
.
 .
.
 принадлежит
принадлежит  . По взаимному расположению векторов
. По взаимному расположению векторов  можно судить о взаимном расположении прямых:
можно судить о взаимном расположении прямых: не параллелен
не параллелен  Две прямые пересекаются в пространстве, если
Две прямые пересекаются в пространстве, если 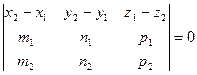
 Две прямые скрещиваются, если векторы
Две прямые скрещиваются, если векторы 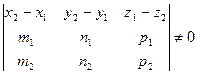
 Обозначим через
Обозначим через  и направляющим вектором прямой
и направляющим вектором прямой  будет равен
будет равен  .
. . Так как угол
. Так как угол 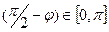 , то синус острого угла между прямой
, то синус острого угла между прямой 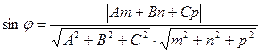
 Если прямая
Если прямая  перпендикулярны, т.е. их скалярное произведение равно 0.
перпендикулярны, т.е. их скалярное произведение равно 0.  , т.е. в координатной форме: Am+Bn+Cp=0.
, т.е. в координатной форме: Am+Bn+Cp=0. Если прямая
Если прямая