|
|
Свойства смешанного произведения
1. Смешанное произведение не меняется при циклической перестановке его сомножителей, т. е. Действительно, в этом случае не изменяется ни объем параллелепипеда, ни ориентация его ребер. 2. Смешанное произведение меняет свой знак при перемене мест любых двух векторов-сомножителей, т. е. Действительно, такая перестановка равносильна перестановке сомножителей в векторном произведении меняющей у произведения знак. 3.Смешанное произведение ненулевых векторов
Выражение смешанного произведения через координаты сомножителей Пусть векторы заданы своими координатами:
Полученную формулу можно записать короче:
так как правая часть равенства представляет собой разложение определителя третьего порядка по элементам третьей строки. Итак, смешанное произведение векторов равно определителю третьего порядка, составленному из координат перемножаемых векторов.
Приложения смешанного произведения 1. Определение взаимной ориентации векторов в пространстве. Если 2. Установление компланарности векторов. Векторы 3. Объем параллелепипеда и треугольной пирамиды. Модуль смешанного произведения численно равен объему параллелепипеда, построенного на векторах
Пример: По координатам вершин пирамиды 1) косинус угола между ребрами 2) площадь треугольника 3) объем пирамиды где Решение: 1) Найдем координаты векторов
Косинус угола между векторами находится по формуле
Ответ: 2) площадь треугольника
Ответ:
3) Найдем объем пирамиды
Ответ:
Прямая на плоскости Линия на плоскости Линия на плоскости рассматривается, как множество точек, обладающих только им присущим геометрическим свойством. Введение декартовой системы координат на плоскости позволяет определить положение произвольной точки ее координатами, а положение линии на плоскости определяется с помощью уравнения. Если уравнение линии имеет вид F(x,y)=0, то любой паре чисел (x,y), удовлетворяющей данному уравнению, соответствует точка М(х,у), принадлежащая линии, и наоборот, координаты любой точки линии обращают ее уравнение в верное тождество. Если две линии на плоскости заданы своими уравнениями Решениям системы соответствуют координаты точки пересечения заданных линий. Простейшей из линий является прямая.
Общее уравнение прямой линии на плоскости Алгебраическое уравнение первой степени относительно х и у задает на плоскости прямую линию Ах + By + С = 0, и называется общим уравнением прямой где А, В, С — произвольные числа, причем А и В не равны нулю одновременно. Некоторые частные случаи общего уравнения прямой: 1) если А = 0, то уравнение имеет вид у = 2) если В = 0. то прямая 3) если С = 0. то получаем Ах + By =0. Уравнению удовлетворяют координаты точки О(0; 0), прямая проходит через начало координат.
Прямая, проходящая через точку, перпендикулярно данному вектору Опр: Вектор, перпендикулярный прямой, называется нормалью к прямой.
Возьмем произвольную точку М(х,у) на прямой. Так как вектор
Полученное уравнение можно преобразовать к виду: Ах+ Ву- Замечание: имея общее уравнение прямой Ах+Ву+С=0, можно выписать координаты нормали к прямой (т.е.вектора, перпендикулярного прямой)
|
|
 .
. ,
,  .
. и
и  равно нулю тогда и только тогда, когда они компланарны.
равно нулю тогда и только тогда, когда они компланарны. ,
, 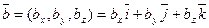 ,
, 
 . Найдем их смешанное произведение, используя формулы для выражения векторного и скалярного произведений:
. Найдем их смешанное произведение, используя формулы для выражения векторного и скалярного произведений: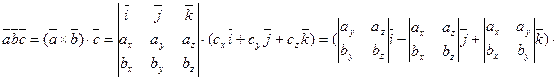
 .
.
 ,то тройка
,то тройка  — правая; если
— правая; если  , то
, то  - левая тройка.
- левая тройка. .
.
 - объем пирамиды, построенной на векторах
- объем пирамиды, построенной на векторах  найти:
найти: и
и  ;
; - основания пирамиды;
- основания пирамиды; ;
;  ;
; 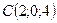 ;
;  .
. и
и  ;
; ,
, 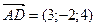
 .
. .
. ,
,  ,
,  .
. .
. ,
,  ,
, ,
,
 кв.ед.
кв.ед. .
. куб.ед.
куб.ед. , то задача о пересечении этих линий сводится к решению системы двух уравнений с двумя переменными:
, то задача о пересечении этих линий сводится к решению системы двух уравнений с двумя переменными: 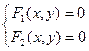
 . Это уравнение прямой, параллельной оси Ох;
. Это уравнение прямой, параллельной оси Ох; параллельна оси Оу;
параллельна оси Оу;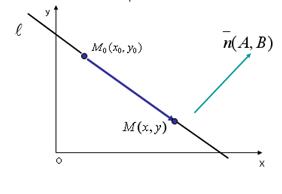 Составим уравнение прямой
Составим уравнение прямой 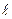 , проходящей через точку
, проходящей через точку  , перпендикулярно ненулевому вектору
, перпендикулярно ненулевому вектору  .
. , то их скалярное произведение равно 0, т.е.
, то их скалярное произведение равно 0, т.е.  , запишем в координатной форме:
, запишем в координатной форме:
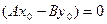
 .
.