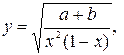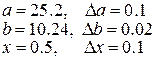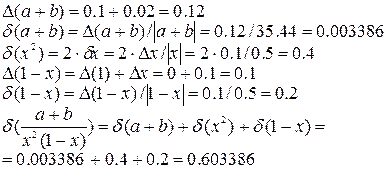|
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНЫМ РАБОТАМ ПО КУРСУ КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕЭ.П. Чен-Син, Л.Н. Панюшева МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНЫМ РАБОТАМ ПО КУРСУ КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ
МОСКВА 2007 Федеральное агентство по образованию
РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ НЕФТИ И ГАЗА им. И.М. ГУБКИНА
Кафедра прикладной математики и компьютерного моделирования
Э.П. Чен-Син, Л.Н. Панюшева МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНЫМ РАБОТАМ ПО КУРСУ КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ Издание 2-е исправленное и дополненное
МОСКВА 2007 УДК 681.3:622.691.4+681.3:622.692.4 Чен-Син Э.П., Панюшева Л.Н. Методические указания к лабораторным работам по курсу Компьютерное моделирование: Учебное пособие. – М.: РГУ нефти и газа, 2007 – 2-е изд. испр. и доп., 94 с.
В данном пособии приводятся задания к лабораторным работам по вариантам в виде технологических задач, требующих решения на компьютере с применением известных численных методов. Для облегчения усвоения материала и лучшего понимания сути применяемых методов решения каждая тема предваряется описанием метода и примерами расчетов. Авторы выражают благодарность профессору Лурье М.В. за помощь в подборе предлагаемых студентам технологических задач. Пособие ориентировано на студентов, изучающих проблемы транспорта нефти и газа, но может с успехом быть использовано и студентами других специальностей, изучающих применение численных методов для решения проблем нефтегазового дела.
Утверждено Советом факультета А и ВТ в качестве учебного пособия.
Рецензенты – Е.В. Гливенко, д.т.н., проф. каф. ПМ и КМ РГУ нефти и газа им. И.М. Губкина, Т.М. Александриди, проф. каф. АСУ МАДИ
Ó Российский государственный университет нефти и газа им. И.М. Губкина, 2004 Ó Российский государственный университет нефти и газа им. И.М. Губкина, 2007 1. Погрешности вычислений 1.1.Основные определения и свойства
Все вычисления, проводимые при решении какой-либо задачи, страдают приближенностью. Это происходит потому, что используемые в этих вычислениях величины несут в себе неточность измерения, определяемую единицей измерения прибора, а также потому, что в процессе вычисления могут производиться округления величин, приводящие также к накоплению погрешности вычисляемых величин. Это надо обязательно учитывать, чтобы всегда иметь представление о величине ошибки полученного результата. Различают два вида погрешностей – абсолютную и относительную. Абсолютная погрешность некоторой величины равна модулю разности между ее истинным значением и приближенным значением, полученным в результате измерения или вычисления. Относительная погрешность – это отношение абсолютной погрешности к модулю приближенного значения величины. Таким образом, если а – приближенное значение величины х, то выражения для абсолютной и относительной погрешностей запишутся соответственно в виде Dх=|х-а|, dх=Dх/| а |
Но так как истинное значение величины х обычно неизвестно, то за величину абсолютной погрешности значения а принимают предельную погрешность Dа, равную верхней оценке модуля абсолютной погрешности, т.е. Исходя из полученных определений погрешностей, можно доказать несколько свойств их, полезных для оценок погрешностей величин, полученных в результате арифметических операций над приближенными значениями. (В приводимых ниже формулах договоримся оценку абсолютной погрешности величины а обозначать Dа, а оценку относительной погрешности этой же величины как dа.) Вот эти свойства:
1. Оценка абсолютной погрешности суммы или разности двух приближенных величин равна сумме оценок их абсолютных погрешностей
2. Если k – точное значение сомножителя некоторой приближенной величины а, то оценка абсолютной погрешности произведения ka равна умноженной на | k| оценке абсолютной погрешности данной величины
3. Оценка относительной погрешности произведения или частного двух приближенных величин равна сумме оценок их относительных погрешностей
4. Оценка относительной погрешности приближенной величины, возведенной в степень, равна произведению оценки относительной погрешности этой величины на модуль показателя степени
5. Если k – точное значение сомножителя некоторой приближенной величины, то оценка относительной погрешности произведения равна оценке относительной погрешности данной величины
6. Оценка относительной погрешности приближенной величины равна отношению оценки ее абсолютной погрешности к модудю приближенного значения этой величины
7. Если известна оценка относительной погрешности величины, то оценку абсолютной погрешности ее можно найти, умножив оценку относительной погрешности на модуль приближенного значения величины
Значащими цифрами приближенного числа называют все цифры в его записи, начиная с первой ненулевой слева. Первые n значащих цифр приближенного числа называют верными (в узком смысле), если абсолютная погрешность этого числа не превышает половины единицы разряда, соответствующего n-й значащей цифре, считая слева направо. Излишние сохраненные цифры, помимо верных, называются сомнительными. Верными значащими цифрами приближенного числа (в широком смысле) называют n его первых значащих цифр, если абсолютная погрешность этого числа не превышает единицы разряда, соответствующего n-й значащей цифре, считая слева направо. Число верных десятичных знаков числа характеризует абсолютную погрешность данного приближенного числа. Так, если известно, что в числе а=0.4357 все цифры верные (в узком смысле), то тогда абсолютная погрешность этого числа не превышает
1.2. Пример (определение верных значащих цифр приближенного числа)
А) Пусть а = 2.3544, В) Пусть а = 12.384,
С) Пусть а = 72.353,
D) Пусть дано число а = 3.29975 и известно, что все его значащие цифры являются верными. И пусть требуется найти его значение с четырьмя значащими верными цифрами (в узком смысле). Округлим его до четырех значащих цифр. Получим а1 = 3.300. При этом │3.29975 – 3.300│= 0.00025 < 0.0005. Следовательно, число 3.300 имеет четыре верных значащих цифры в узком смысле, хотя его три последние цифры не совпадают с таковыми в исходном числе.
Надо иметь в виду, что, имея дело с приближенными числами, следует в итоговых таблицах указывать верные цифры. По ним же давать и абсолютные погрешности.
1.3. Пример
Пусть необходимо вычислить значение величины y ,а также оценить погрешность этого вычисления. При этом известны оценки абсолютных погрешностей используемых в вычислении величин Дано:
Тогда проделаем следующие расчеты:
Найдем верные значащие цифры числа y (в широком смысле). Абсолютная погрешность его равна приближенно ∆y = 5.08 < 10. Следовательно, в данном числе количество значащих цифр надо уменьшить до двух. Округлим его, получим y1 = 20. Посчитаем получающуюся абсолютную погрешность, она равна ∆y1 = 5.0799224 + 3.161948 ≈ 8.2 1.4. Лабораторная работа №1 |
|
 . В этом случае истинное значение х находится в интервале (а – Dа, а +Dа). Аналогично поступают с относительной погрешностью.
. В этом случае истинное значение х находится в интервале (а – Dа, а +Dа). Аналогично поступают с относительной погрешностью.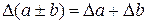
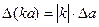
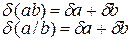
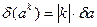
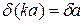
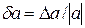
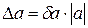
 0.00005.
0.00005.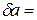 0.002. Тогда
0.002. Тогда  = 0.00471. В широком смысле верны три цифры. Округлим это число до трех значащих цифр, получим а1 = 2.35 ,
= 0.00471. В широком смысле верны три цифры. Округлим это число до трех значащих цифр, получим а1 = 2.35 , 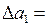
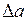 +
+ 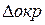 = 0.00471+0.0044 = 0.00911 < 0.01. В округлении числа все 3 цифры верные в широком смысле.
= 0.00471+0.0044 = 0.00911 < 0.01. В округлении числа все 3 цифры верные в широком смысле.