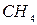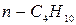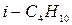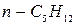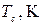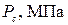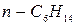Оценка погрешностей результата вычислений
Оценить абсолютную и относительную погрешности результатов вычисления выражений ( V, S, Y ), если известны оценки абсолютных погрешностей измерения участвующих в выражениях величин:
2. Методы решения нелинейных уравнений
2.1.Общие сведения
Мы рассмотрим здесь лишь некоторые наиболее используемые методы решения нелинейных уравнений. Эти методы относятся к итерационным методам, т.е. методам получения последовательности точек 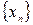 , которая сходится к решению уравнения , которая сходится к решению уравнения 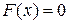 . .
При этом итерационный процесс останавливается тогда, когда достигается заданная точность 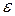 полученного результата. Говоря о точности, можно требовать получения такого приближения корня уравнения, что модуль значения функции полученного результата. Говоря о точности, можно требовать получения такого приближения корня уравнения, что модуль значения функции 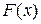 отличается от нуля не больше, чем на заданную малую величину отличается от нуля не больше, чем на заданную малую величину 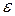 , т.е. , т.е. 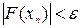 . .
А можно требовать локализации самого корня уравнения на отрезке так, чтобы ошибка определения корня была не больше 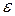 , т.е. остановка будет производиться при нахождении такого отрезка , т.е. остановка будет производиться при нахождении такого отрезка  , содержащего корень, что длина его будет не больше , содержащего корень, что длина его будет не больше 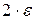 . Тогда, взяв в качестве корня середину этого отрезка, можно быть уверенным, что истинный корень уравнения отличается от найденного не больше, чем на . Тогда, взяв в качестве корня середину этого отрезка, можно быть уверенным, что истинный корень уравнения отличается от найденного не больше, чем на 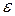 , т.е. , т.е. 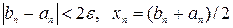 . .
2.1.1. Метод хорд
Этим методом можно пользоваться в том случае, если функция 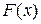 непрерывна в некоторой окрестности корня уравнения. непрерывна в некоторой окрестности корня уравнения.
Для начала ищется отрезок 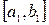 в этой окрестности, который содержал бы только один искомый корень уравнения, а значения функции на концах его были бы разных знаков. Так как функция непрерывна на этом отрезке, то ее график обязательно где-то внутри этого отрезка пересечет ось абсцисс. Эту точку х пересечения графика функции с осью ОХ, являющуюся корнем уравнения, и нужно найти. в этой окрестности, который содержал бы только один искомый корень уравнения, а значения функции на концах его были бы разных знаков. Так как функция непрерывна на этом отрезке, то ее график обязательно где-то внутри этого отрезка пересечет ось абсцисс. Эту точку х пересечения графика функции с осью ОХ, являющуюся корнем уравнения, и нужно найти.
Затем строится хорда, соединяющая точки графика функции, отвечающие концам имеющегося отрезка. Вычисляется точка пересечения этой хорды с осью ОХ. Назовем эту точку х1. Затем определяется, на каком из отрезков 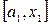 или или  лежит корень уравнения. Если лежит корень уравнения. Если 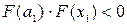 , то корень лежит на отрезке , то корень лежит на отрезке 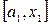 и и  становится правым концом нового (уже меньшего) отрезка локализации корня, а становится правым концом нового (уже меньшего) отрезка локализации корня, а  – левым концом этого отрезка. При этом производят переименование – левым концом этого отрезка. При этом производят переименование 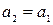 и и 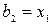 . .
Если 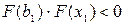 , то корень – на отрезке , то корень – на отрезке  и и  становится левым концом нового отрезка локализации корня, а становится левым концом нового отрезка локализации корня, а 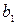 – правым концом этого отрезка, т.е. – правым концом этого отрезка, т.е.  и и  . .
Теперь имеется уже новый отрезок локализации корня. С ним проделывается та же процедура построения хорды и поиска точки ее пересечения с осью ОХ – точки  . Остановка производится при нахождении такого приближения . Остановка производится при нахождении такого приближения  , что , что 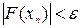 . .
Этот процесс можно увидеть на рис.1.
Рис.1
Формула для получения точки пересечения хорды с осью ОХ на каждом шаге имеет следующий вид:
 . Часто вместо этого метода используют метод деления пополам, где очередное приближение находят по формуле . Часто вместо этого метода используют метод деления пополам, где очередное приближение находят по формуле  . При этом отрезок локализации по длине можно сжать до какого угодно наперед заданного значения. Поэтому остановка процесса может быть произведена при выполнении условия . При этом отрезок локализации по длине можно сжать до какого угодно наперед заданного значения. Поэтому остановка процесса может быть произведена при выполнении условия  . .
2.1.2. Метод касательных Ньютона
Этот метод можно использовать в случае выполнения следующих требований к функции 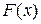 : :
1) На найденном отрезке локализации корня 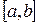 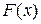 должна иметь единственный корень и значения функции на концах этого отрезка должны быть разных знаков, т.е. должна иметь единственный корень и значения функции на концах этого отрезка должны быть разных знаков, т.е. 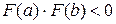 . .
2) 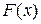 должна иметь непрерывную вторую производную на этом отрезке. должна иметь непрерывную вторую производную на этом отрезке.
3) Кроме того, на отрезке 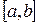 вторая производная функции вторая производная функции
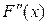 должна сохранять свой знак. должна сохранять свой знак.
Тогда в качестве начального приближения корня выбирается  по следующему правилу: по следующему правилу: 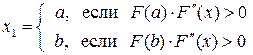
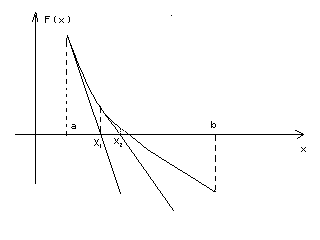
Затем в точке с абсциссой  строится касательная к графику функции строится касательная к графику функции 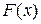 . Точка пересечения этой касательной с осью ОХ берется в качестве следующего приближения корня . Точка пересечения этой касательной с осью ОХ берется в качестве следующего приближения корня  . И так процесс продолжается до тех пор, пока не будет достигнута нужная точность . И так процесс продолжается до тех пор, пока не будет достигнута нужная точность 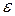 . .
Если достаточно получить точку, в которой 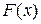 не превышает по модулю заданное число не превышает по модулю заданное число 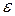 , то производят остановку при выполнении этого условия. , то производят остановку при выполнении этого условия.
Если же надо получить приближение корня, отстоящее от истинного его значения не более чем на 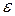 , то процесс останавливают тогда, когда выполняется следующее условие: , то процесс останавливают тогда, когда выполняется следующее условие:
  , где , где
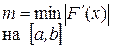 и и 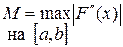
Процесс можно увидеть на рис.2.
Рис.2
Формула для вычисления точки пересечения касательной с осью ОХ имеет следующий вид:

2.1.3. Пример 1
Вычислим с помощью метода хорд корень уравнения 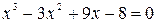 с точностью с точностью 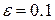 . Под точностью будем понимать отклонение модуля функции от нулевого значения. . Под точностью будем понимать отклонение модуля функции от нулевого значения.
Выберем в качестве левой границы отрезка 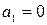 . При этом . При этом 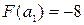 . В качестве правой границы можно взять . В качестве правой границы можно взять  . При этом . При этом  . Выполняется необходимое условие . Выполняется необходимое условие 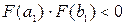 . .
Найдем первое приближение корня 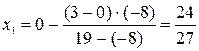 
Найдем значение функции в этой точке
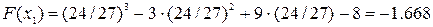
Проверим, не надо ли прекратить вычисления:
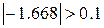 , значит, точность еще не достигнута. , значит, точность еще не достигнута.
Т.к. 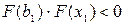 , следующим отрезком будет , следующим отрезком будет 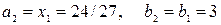 . .
Найдем второе приближение корня
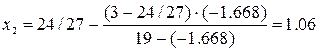
Найдем значение функции в этой точке
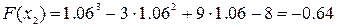 . .
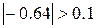 , поэтому продолжаем вычисления. , поэтому продолжаем вычисления.
Т.к.  , следующим отрезком будет , следующим отрезком будет
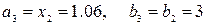 . И т.д. до достижения заданной точности. . И т.д. до достижения заданной точности.
2.1.4. Пример 2
Вычислим с помощью метода Ньютона корень уравнения 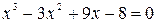 с точностью с точностью 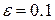 . .
Под точностью будем понимать отклонение модуля функции от нулевого значения.
Выберем в качестве левой границы отрезка 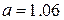 . Значение функции в этой точке равно . Значение функции в этой точке равно 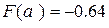 . В качестве правой границы можно взять . В качестве правой границы можно взять 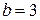 . Значение функции в этой точке равно . Значение функции в этой точке равно  . А значит, выполняется необходимое условие применения метода . А значит, выполняется необходимое условие применения метода 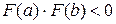 . .
Кроме этого выполняется требование непрерывности второй производной функции: 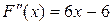 – непрерывная функция. – непрерывная функция.
А также на выбранном отрезке вторая производная функции 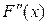 не меняет знак. Действительно, не меняет знак. Действительно, 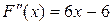 больше нуля на всем отрезке больше нуля на всем отрезке 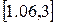 . .
Выберем в качестве первого приближения 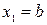 , т.к. , т.к. 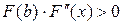 . .
Найдем второе приближение корня
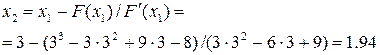
Значение функции в этой точке равно
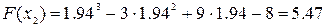
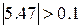 поэтому продолжаем и ищем третье приближение корня поэтому продолжаем и ищем третье приближение корня
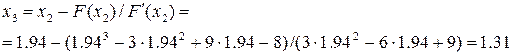
Значение функции в этой точке равно
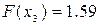
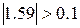 поэтому продолжаем и ищем четвертое приближение корня поэтому продолжаем и ищем четвертое приближение корня
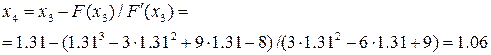
Значение функции в этой точке равно
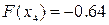
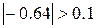 .И так далее до достижения точности. .И так далее до достижения точности.
2.2. Лабораторная работа №2
Решение нелинейного уравнения методом хорд
2.2.1. Задача №1
Воспользовавшись методом хорд для нахождения корня нелинейного уравнения, вычислить коэффициент гидравлического сопротивления 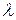 при течении жидкости в трубопроводе с относительной шероховатостью внутренней стенки при течении жидкости в трубопроводе с относительной шероховатостью внутренней стенки 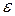 для заданного числа Рейнольдса Re. для заданного числа Рейнольдса Re.
Универсальный закон сопротивления для развитого турбулентного течения имеет вид:
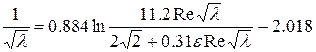
Данные по вариантам:
| № варианта
| шероховатость 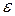
| число Рейнольдса Re
| |
| 
| 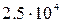
| |
| 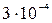
| 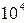
| |
| 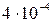
| 
| |
| 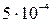
| 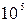
| |
| 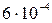
| 
| |
| 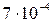
| 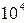
| |
| 
| 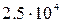
| |
| 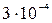
| 
| |
| 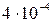
| 
| |
| 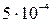
| 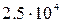
| |
| 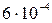
| 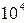
| |
| 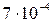
| 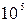
| |
| 
| 
| |
| 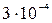
| 
| |
| 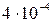
| 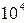
| |
| 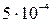
| 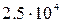
| |
| 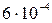
| 
| |
| 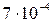
| 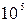
| |
| 
| 
| |
| 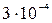
| 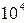
| |
| 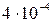
| 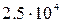
| |
| 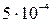
| 
| |
| 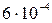
| 
| |
| 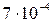
| 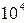
|
2.2.2. Задача №2
Воспользовавшись методом хорд для нахождения корня нелинейного уравнения, вычислить расход дизельного топлива Q( 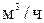 ) плотностью ) плотностью  и кинематической вязкостью и кинематической вязкостью  при перекачке по участку трубопровода длиной L= 125 км, диаметром d = 514 мм и с шероховатостью внутренней стенки при перекачке по участку трубопровода длиной L= 125 км, диаметром d = 514 мм и с шероховатостью внутренней стенки 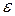 = 0.0005, если насосная станция работает с двумя последовательно включенными насосными агрегатами. = 0.0005, если насосная станция работает с двумя последовательно включенными насосными агрегатами.
Уравнение баланса напоров для участка трубопровода имеет вид:
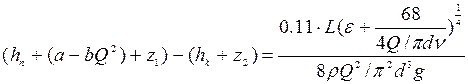 , ,
где 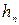 и и 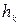 – подпор перед станцией и напор в конце участка соответственно; – подпор перед станцией и напор в конце участка соответственно;
a и b – коэффициенты, определяемые типом и количеством насосов;
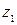 и и  – высотные отметки сечений трубопровода в начале и в конце участка. – высотные отметки сечений трубопровода в начале и в конце участка.
Данные по вариантам:
| №
вар.
| 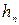 , м , м
| 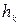 , м , м
| a, м
| b, 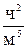
| 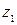 , м , м
|  , м , м
| |
|
|
|
| 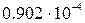
|
|
| |
|
|
|
| 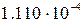
|
|
| |
|
|
|
| 
|
|
| |
|
|
|
| 
|
|
| |
|
|
|
| 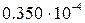
|
|
| |
|
|
|
| 
|
|
| |
|
|
|
| 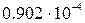
|
|
| |
|
|
|
| 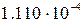
|
|
| |
|
|
|
| 
|
|
| |
|
|
|
| 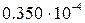
|
|
|
2.2.3. Задача №3
Состояние реального газа может быть описано уравнением Ван-дер-Ваальса:
 , где , где
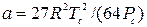 , ,
 , ,
R – универсальная газовая постоянная,
T – температура газа,
Pc – критическое давление,
Tc – критическая температура,
V – молярный объем газа.
Воспользовавшись методом деления пополам для нахождения корня нелинейного уравнения, найти молярный объем данного газа V при заданных значениях давления P итемпературы T.
Величины критических параметров Pc и Tc отдельных газов приведены с следующей таблице:
| газ
| метан
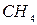
| этан

| пропан

| n-бутан
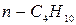
| i-бутан
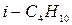
| n-пентан
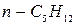
| 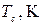
| 190,55
| 305,43
| 369,82
| 408,13
| 425,16
| 469,65
| 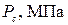
| 4,695
| 4,976
| 4,333
| 3,871
| 3,719
| 3,435
|
| Газ
| i-пентан

| n-гексан
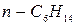
| 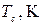
| 460,39
| 507,35
| 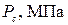
| 3,448
| 3,072
|
Задания по вариантам:
| № вар.
|
|
|
|
|
|
| | Газ
| Метан
| этан
| пропан
| n-бутан
| i-бутан
| n-пентан
| | Т, К
|
|
|
|
|
|
| | Р, МПа
| 2,200
| 3,700
| 1,570
| 1,800
| 1,250
| 2,400
| | № вар.
|
|
|
|
|
|
| | газ
| i-пентан
| n-гексан
| метан
| этан
| n-бутан
| пропан
| | Т, К
|
|
|
|
|
|
| | Р, МПа
| 2,250
| 2,500
| 1,750
| 2,370
| 1,600
| 1,590
| | | | | | | | | | | | |
2.3. Лабораторная работа №3
|
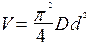
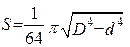
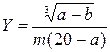
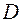
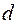
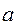


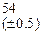
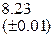
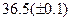
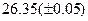

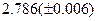



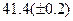
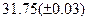

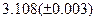
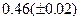

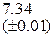
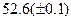
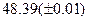
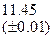

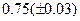
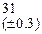
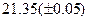
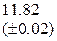
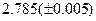


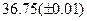


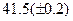
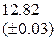
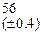

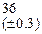
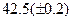
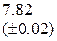

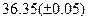
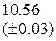
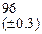
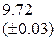

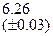
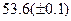
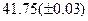
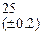
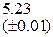
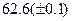


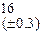
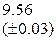
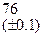
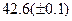

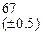
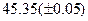
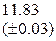
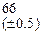
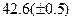
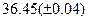

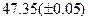
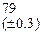
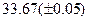
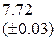




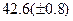



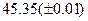
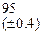
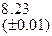
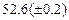
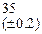
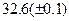
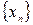 , которая сходится к решению уравнения
, которая сходится к решению уравнения 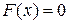 .
.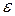 полученного результата. Говоря о точности, можно требовать получения такого приближения корня уравнения, что модуль значения функции
полученного результата. Говоря о точности, можно требовать получения такого приближения корня уравнения, что модуль значения функции 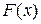 отличается от нуля не больше, чем на заданную малую величину
отличается от нуля не больше, чем на заданную малую величину 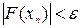 .
. , содержащего корень, что длина его будет не больше
, содержащего корень, что длина его будет не больше 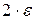 . Тогда, взяв в качестве корня середину этого отрезка, можно быть уверенным, что истинный корень уравнения отличается от найденного не больше, чем на
. Тогда, взяв в качестве корня середину этого отрезка, можно быть уверенным, что истинный корень уравнения отличается от найденного не больше, чем на 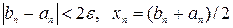 .
.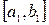 в этой окрестности, который содержал бы только один искомый корень уравнения, а значения функции на концах его были бы разных знаков. Так как функция непрерывна на этом отрезке, то ее график обязательно где-то внутри этого отрезка пересечет ось абсцисс. Эту точку х пересечения графика функции с осью ОХ, являющуюся корнем уравнения, и нужно найти.
в этой окрестности, который содержал бы только один искомый корень уравнения, а значения функции на концах его были бы разных знаков. Так как функция непрерывна на этом отрезке, то ее график обязательно где-то внутри этого отрезка пересечет ось абсцисс. Эту точку х пересечения графика функции с осью ОХ, являющуюся корнем уравнения, и нужно найти.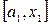 или
или  лежит корень уравнения. Если
лежит корень уравнения. Если 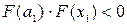 , то корень лежит на отрезке
, то корень лежит на отрезке  становится правым концом нового (уже меньшего) отрезка локализации корня, а
становится правым концом нового (уже меньшего) отрезка локализации корня, а  – левым концом этого отрезка. При этом производят переименование
– левым концом этого отрезка. При этом производят переименование 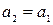 и
и 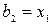 .
.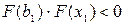 , то корень – на отрезке
, то корень – на отрезке 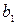 – правым концом этого отрезка, т.е.
– правым концом этого отрезка, т.е.  и
и  .
. . Остановка производится при нахождении такого приближения
. Остановка производится при нахождении такого приближения  , что
, что 
 . Часто вместо этого метода используют метод деления пополам, где очередное приближение находят по формуле
. Часто вместо этого метода используют метод деления пополам, где очередное приближение находят по формуле  . При этом отрезок локализации по длине можно сжать до какого угодно наперед заданного значения. Поэтому остановка процесса может быть произведена при выполнении условия
. При этом отрезок локализации по длине можно сжать до какого угодно наперед заданного значения. Поэтому остановка процесса может быть произведена при выполнении условия  .
.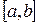
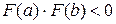 .
.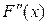 должна сохранять свой знак.
должна сохранять свой знак. по следующему правилу:
по следующему правилу: 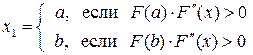

 , где
, где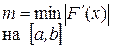 и
и 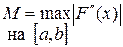

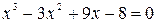 с точностью
с точностью 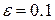 . Под точностью будем понимать отклонение модуля функции от нулевого значения.
. Под точностью будем понимать отклонение модуля функции от нулевого значения.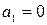 . При этом
. При этом 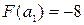 . В качестве правой границы можно взять
. В качестве правой границы можно взять  . При этом
. При этом  . Выполняется необходимое условие
. Выполняется необходимое условие 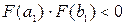 .
.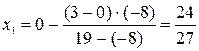
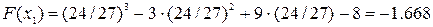
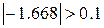 , значит, точность еще не достигнута.
, значит, точность еще не достигнута.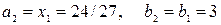 .
.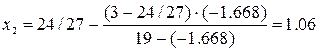
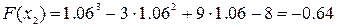 .
.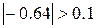 , поэтому продолжаем вычисления.
, поэтому продолжаем вычисления. , следующим отрезком будет
, следующим отрезком будет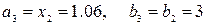 . И т.д. до достижения заданной точности.
. И т.д. до достижения заданной точности.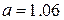 . Значение функции в этой точке равно
. Значение функции в этой точке равно 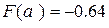 . В качестве правой границы можно взять
. В качестве правой границы можно взять 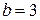 . Значение функции в этой точке равно
. Значение функции в этой точке равно  . А значит, выполняется необходимое условие применения метода
. А значит, выполняется необходимое условие применения метода 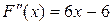 – непрерывная функция.
– непрерывная функция.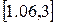 .
.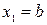 , т.к.
, т.к. 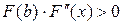 .
.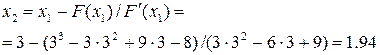
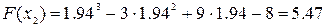
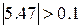 поэтому продолжаем и ищем третье приближение корня
поэтому продолжаем и ищем третье приближение корня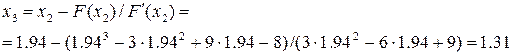
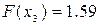
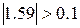 поэтому продолжаем и ищем четвертое приближение корня
поэтому продолжаем и ищем четвертое приближение корня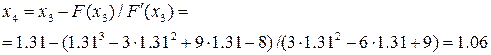
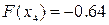
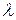 при течении жидкости в трубопроводе с относительной шероховатостью внутренней стенки
при течении жидкости в трубопроводе с относительной шероховатостью внутренней стенки 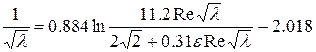

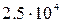
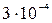
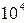
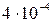

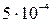
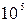
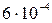

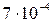
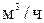 ) плотностью
) плотностью  и кинематической вязкостью
и кинематической вязкостью  при перекачке по участку трубопровода длиной L= 125 км, диаметром d = 514 мм и с шероховатостью внутренней стенки
при перекачке по участку трубопровода длиной L= 125 км, диаметром d = 514 мм и с шероховатостью внутренней стенки 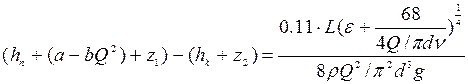 ,
,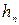 и
и 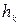 – подпор перед станцией и напор в конце участка соответственно;
– подпор перед станцией и напор в конце участка соответственно;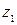 и
и  – высотные отметки сечений трубопровода в начале и в конце участка.
– высотные отметки сечений трубопровода в начале и в конце участка.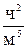
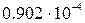
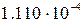


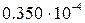
 , где
, где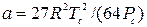 ,
, ,
,