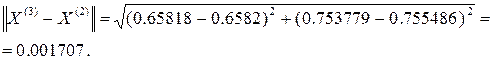|
|
Решение нелинейного уравнения методом Ньютона
2.3.1. Задача №1
Вычислить перепад давления Известна формула Букингема, связывающая
Вычисления провести, воспользовавшись методом Ньютона для решения нелинейного уравнения.
Задания по вариантам:
2.3.2. Задача №2 Резервуар для нефти имеет форму лежащего цилиндра радиусом 1м и длиной 3м. Для определения степени заполнения резервуара нефтью в него опускается вертикально в отверстие сверху измерительный стержень. Необходимо рассчитать шкалу для этого стержня, на которой были бы нанесены отметки о заполнении резервуара в долях q от его полного объема (для q= 0.02; 0.04; 0.06;…; 0.50, т.е. для заполнения на 2%, 4%, 6%, …, 50%). Для этого надо определить высоты всех указанных уровней заполнения.
Решение:
Пусть l – длина резервуара, a – угол при вершине треугольника, образованного при соединении центра окружности поперечного сечения резервуара и концов линии поверхности жидкости ( рис. 3). Рис. 3
При этом заполненный объем V есть функция угла a:
Высота уровня жидкости вычисляется по формуле
С другой стороны имеем
Из формул (1) и (3) получаем уравнение
решая которое методом Ньютона, найдем a. Подставив значение a в формулу (2), найдем h. Каждый студент должен выполнить расчет уровня жидкости h для заданного значения q. Затем вся группа строит искомую шкалу. Задания по вариантам:
2.3.3. Задача №3
Состояние реального газа в простейшем случае может быть описано уравнением Редлиха-Квонга:
R – универсальная газовая постоянная, T – температура газа, Pc – критическое давление, Tc – критическая температура, V – молярный объем газа.
Воспользовавшись методом Ньютона для нахождения корня нелинейного уравнения, найти молярный объем данного газа при заданных значениях P и T. Критические параметры отдельных газов даны в следующей таблице:
Задания по вариантам:
3. Методы решения систем линейных уравнений 3.1. Основные понятия Рассмотрим систему n линейных алгебраических уравнений с n неизвестными:
В ней aij – коэффициенты при неизвестных xj. Решением этой системы называется такой набор значений неизвестных xj, который удовлетворяет системе. Коэффициенты aij можно записать в виде матрицы (таблицы):
Известно, что такая система имеет единственное решение тогда и только тогда, когда матрица системы невырожденная, т.е. Для решения таких систем используются как прямые методы, в которых получают точные значения неизвестных после применения заранее известного числа операций, так и итерационные методы, в которых число шагов (итераций) заранее неизвестно, и на каждом шаге получают некоторое приближенное решение системы до тех пор, пока не будет получено решение с нужной точностью.
3.1.1. Метод Гаусса
Этот метод относится к прямым методам решения линейных систем. Он основан на приведении матрицы системы к треугольному виду путем последовательного исключения неизвестных из уравнений системы (прямой ход метода Гаусса) и последующем решении этой треугольной системы, начиная с последнего уравнения (обратный ход метода Гаусса). Сначала с помощью первого уравнения исключается Этот процесс называется прямым ходом Гаусса и продолжается до тех пор, пока в левой части последнего (n-го) уравнения не останется лишь один член с неизвестным Если на каком-то этапе этого процесса оказывается, что очередной исключаемой переменной уже нет ни в одном из последующих уравнений, то матрица системы является вырожденной, и метод Гаусса в этом случае неприменим. Обратный ход метода Гаусса состоит в последовательном вычислении неизвестных. Решая последнее уравнение, находят единственное неизвестное Рассмотрим применение метода Гаусса для системы из трех уравнений:
Для исключения
Теперь из третьего уравнения системы (2) нужно исключить
Матрица системы (3) имеет треугольный вид. На этом завершается прямой ход метода Гаусса. Заметим, о чем уже говорилось выше, что в процессе исключения неизвестных приходится выполнять операции деления на Обратный ход начинается с решения третьего уравнения системы (3):
Используя это значение, можно найти
Аналогично строится вычислительный алгоритм для линейной системы с другим числом неизвестных.
3.1.2. Итерационные методы Для применения итерационных методов необходимо предварительно исходную систему уравнений (1) привести к виду:
Этот вид получается, если из первого уравнения выразить x1, из второго x2 и т.д.:
Пусть
1) Метод простой итерации В этом методе коэффициенты вектора
2) Метод Гаусса-Зейделя В этом методе коэффициенты вектора
Для сходимости итерационного процесса достаточно, чтобы модули диагональных коэффициентов для каждого уравнения системы были не меньше сумм модулей всех остальных коэффициентов:
При этом хотя бы для одного уравнения неравенство должно выполняться строго. Эти условия являются достаточными, но не необходимыми, т.е. для некоторых систем итерационный процесс сходится и при нарушении этих условий. Процесс итерационных вычислений прекращают, когда разница между двумя последовательными приближенными решениями становится достаточно малой, т.е.
3.1.3. Пример 1
Найдем решение следующей линейной системы методом Гаусса:
Сначала с помощью первого уравнения исключим x1 из второго и третьего уравнений. Это можно сделать так, как было описано выше. Но мы для простоты понимания проделаем это в два этапа. Сначала сделаем коэффициенты перед переменной x1 во всех уравнениях равными единице, поделив каждое уравнение на коэффициент, стоящий перед этой переменной. Т.е. поделив первое на 2, второе на 2, а третье на 4. Поместив слева схему производимых действий, запишем полученную систему, эквивалентную исходной:
Теперь избавимся от переменной x1 во втором и третьем уравнениях, вычтя из них первое:
Теперь нам нужно с помощью второго уравнения избавиться от переменной x2 в третьем уравнении. Сделаем это тоже в два этапа. Сначала поделим второе уравнение на 0.5, а третье уравнение на -1.75. Получим систему:
Далее преобразуем третье уравнение, вычтя из него второе:
На данном этапе система приведена к треугольному виду. Найдем значения неизвестных, начиная с третьего уравнения.
Сделаем проверку, подставив полученные значения неизвестных в левые части уравнений системы, чтобы убедиться в выполнении условий:
3.1.4. Пример 2 Найдем решение той же системы методом простой итерации, предварительно преобразовав ее так, чтобы выполнялись достаточные условия сходимости. Имеем систему:
Поставим в ней третье уравнение на первое место, второе уравнение – на третье место, а на втором месте запишем разность второго уравнения и удвоенного первого:
Для такой системы достаточные условия сходимости уже выполняются. Выразим неизвестные из уравнений, как это предлагается в методе:
Пусть первым приближением решения будет вектор
Таким образом, имеем следующее приближение решения:
Таким образом,
Таким образом, Посчитаем разницу между двумя последними приближенными решениями, взяв в качестве
3.2. Лабораторная работа №4 Решение системы линейных уравнений
Решить систему линейных уравнений а) методом Гаусса, б) методом простой итерации.
Данные по вариантам:
4. Решение систем нелинейных уравнений 4.1. Основные понятия В общем случае систему нелинейных уравнений можно представить в виде:
В отличие от систем линейных уравнений не существует прямых методов решения нелинейных систем общего вида. Лишь в отдельных случаях систему (1) можно решить непосредственно. Для решения систем нелинейных уравнений обычно используются итерационные методы. К таким методам относятся метод простой итерации и метод Ньютона. 4.1.1. Метод простой итерации
Система уравнений (1) приводится предварительно к следующему виду:
В качестве начального приближения выбирается произвольный вектор Для нахождения последующих приближенных решений используют формулы: а). Метод Якоби:
В данном случае для расчета координат последующего приближения координаты предыдущего подставляются в формулы (2).
б). Метод Гаусса-Зейделя:
в). Метод верхней релаксации:
где Достаточное условие сходимости методов простой итерации в области G для любого начального приближения
4.1.2.Метод Ньютона
Применяется для систем вида (1). Пусть
где
Если Рассмотрим отдельно случай двух уравнений с двумя неизвестными и выведем формулы для вычисления. Пусть имеется система: Введем обозначения
Или, после перемножения стоящих справа в этом уравнении матрицы и вектора, имеем:
Но
(Обозначим этот определитель символом
(Обозначим этот определитель символом Запишем тогда в наших обозначениях формулы покоординатно:
4.1.3. Пример 1
Решим систему двух нелинейных уравнений методом простой итерации с применением формулы Якоби:
Для этого запишем ее в виде: В качестве начального приближения возьмем вектор
Посчитаем норму разности двух последних приближений:
Если такая точность достаточна, то вычисления прекращают и за искомое решение принимают последнюю найденную точку, т.е.
4.1.4. Пример 2
Решим ту же систему методом Ньютона, предварительно записав ее в требуемом виде
Возьмем в качестве начального приближения
Получаем
Для следующего приближения:
Отсюда
Для третьей итерации:
Отсюда
Сравниваем два последних приближения:
Как хорошо видно, метод Ньютона дает более быструю сходимость по сравнению с методом простой итерации.
4.2. Лабораторная работа № 5 |
|
 , который необходим для того, чтобы перекачивать с расходом
, который необходим для того, чтобы перекачивать с расходом  по трубопроводу радиусом
по трубопроводу радиусом 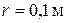 , длиной
, длиной  в ламинарном режиме высоковязкий застывающий мазут плотностью
в ламинарном режиме высоковязкий застывающий мазут плотностью  , если он при выбранной температуре бингамовский пластик с предельным напряжением сдвига
, если он при выбранной температуре бингамовский пластик с предельным напряжением сдвига  и кинематической вязкостью
и кинематической вязкостью 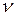 .
. .
.


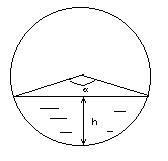
 (1)
(1) (2)
(2) (3)
(3) , (4)
, (4) , где
, где
 ,
, ,
,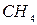


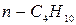
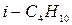
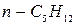
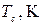
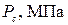

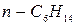
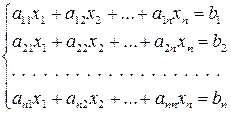
 , правую часть системы в виде вектора
, правую часть системы в виде вектора  , а неизвестные в виде вектора
, а неизвестные в виде вектора  . Тогда систему можно записать в виде матрично-векторного уравнения
. Тогда систему можно записать в виде матрично-векторного уравнения  .
. (определитель матрицы
(определитель матрицы  не равен нулю).
не равен нулю). из всех последующих уравнений системы. Затем с помощью второго уравнения исключается
из всех последующих уравнений системы. Затем с помощью второго уравнения исключается  из третьего и всех последующих уравнений и т.д. При этом, если в уравнении с номером k отсутствует неизвестная
из третьего и всех последующих уравнений и т.д. При этом, если в уравнении с номером k отсутствует неизвестная  (
(  ), то производится перестановка этого уравнения с любым нижестоящим уравнением, содержащим эту переменную.
), то производится перестановка этого уравнения с любым нижестоящим уравнением, содержащим эту переменную. .
. и т.д. Последним находят
и т.д. Последним находят  (1)
(1) . Затем, умножив первое уравнение на
. Затем, умножив первое уравнение на  и прибавив результат к третьему уравнению, также исключим из него
и прибавив результат к третьему уравнению, также исключим из него  (2)
(2)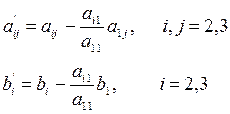
 и прибавим результат к третьему. Получим:
и прибавим результат к третьему. Получим: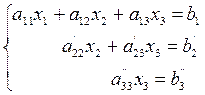 (3)
(3)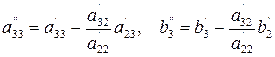
 и т.д. Поэтому они должны быть отличны от нуля; в противном случае необходимо соответственным образом переставить уравнения системы.
и т.д. Поэтому они должны быть отличны от нуля; в противном случае необходимо соответственным образом переставить уравнения системы.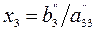
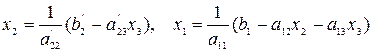

 ,
,  ,
,  ,
,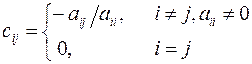
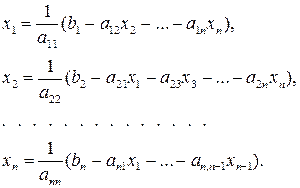
 – некий произвольно задаваемый вектор начального приближения к решению системы. Тогда для нахождения последующих приближений
– некий произвольно задаваемый вектор начального приближения к решению системы. Тогда для нахождения последующих приближений  , где m – номер итерации, а
, где m – номер итерации, а 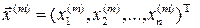 , можно применить один из следующих известных методов: метод простой итерации, метод Гаусса-Зейделя, метод верхней релаксации.
, можно применить один из следующих известных методов: метод простой итерации, метод Гаусса-Зейделя, метод верхней релаксации.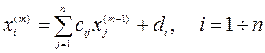


 где
где  заданная точность, а
заданная точность, а  , либо
, либо  .
.

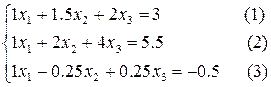

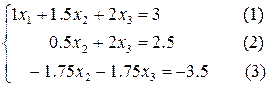

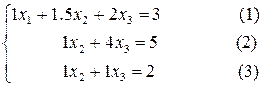

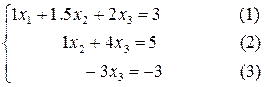
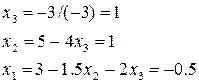
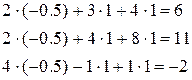
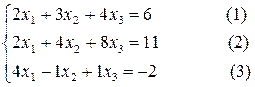


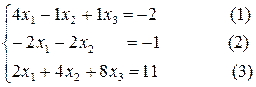
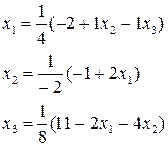
 . Тогда следующее приближение рассчитаем по полученным формулам:
. Тогда следующее приближение рассчитаем по полученным формулам: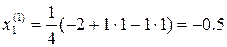
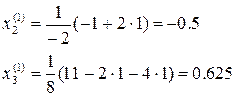
 . Следующее приближение:
. Следующее приближение: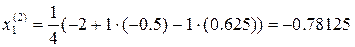
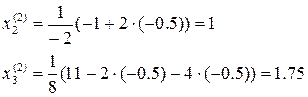
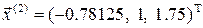 . Далее
. Далее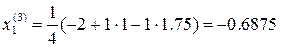
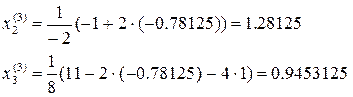
 .
. :
:  . Тогда
. Тогда 
 . В этом случае, если точность, например,
. В этом случае, если точность, например, 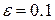 , то процесс вычислений останавливается. Если же требуется более точное приближение, то вычисления продолжают.
, то процесс вычислений останавливается. Если же требуется более точное приближение, то вычисления продолжают.




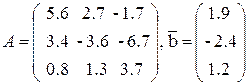
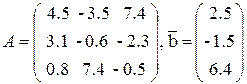





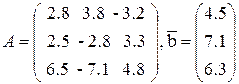
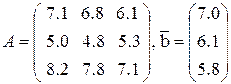
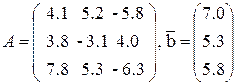






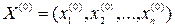 .
. где верхний индекс отмечает номер итерации.
где верхний индекс отмечает номер итерации. В этом методе для расчета каждой следующей координаты
В этом методе для расчета каждой следующей координаты  используются уточненные значения предыдущих координат, уже полученных на данной итерации:
используются уточненные значения предыдущих координат, уже полученных на данной итерации:  , а также неуточненные оставшиеся координаты:
, а также неуточненные оставшиеся координаты:  , полученные из предыдущего приближения.
, полученные из предыдущего приближения.
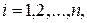
 уточненное значение переменной по Гауссу-Зейделю,
уточненное значение переменной по Гауссу-Зейделю,  параметр релаксации,
параметр релаксации,  .
. , имеет вид:
, имеет вид:
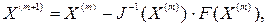
 ,
, обратная матрица для матрицы Якоби
обратная матрица для матрицы Якоби  в точке
в точке  :
: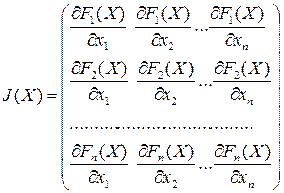
 то в достаточно малой окрестности корня
то в достаточно малой окрестности корня  итерационный процесс сходится. В качестве критерия окончания итераций используют условие
итерационный процесс сходится. В качестве критерия окончания итераций используют условие  , например,
, например,  .
. и
и  . Тогда
. Тогда  . Обратной матрицей к Якобиану
. Обратной матрицей к Якобиану  .
. ,
,  . Тогда рекурентную формулу для расчета приближенного решения можно записать в следующем матрично-векторном виде:
. Тогда рекурентную формулу для расчета приближенного решения можно записать в следующем матрично-векторном виде: .
. .
.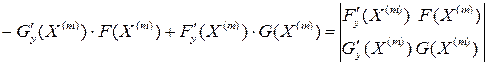
 ),
),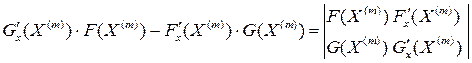
 ).
). .
. .
. .
. . Тогда
. Тогда  , аналогично
, аналогично  и
и .
.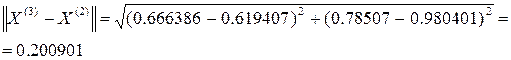
 . В противном случае расчеты продолжают.
. В противном случае расчеты продолжают. . Получим:
. Получим: , где
, где , а
, а  .
. вблизи искомого решения. Тогда
вблизи искомого решения. Тогда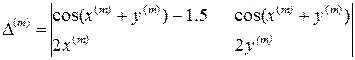
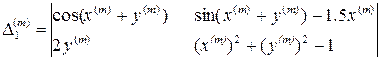
 .
. . Отсюда
. Отсюда 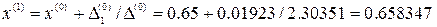
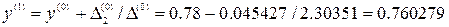 .
. .
.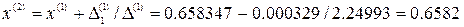
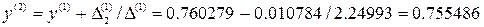 .
.
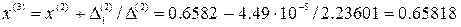
 .
.