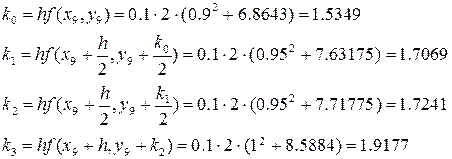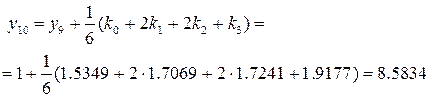|
|
Вычисление определенного интеграла методом трапеций6.3.1.Задача №1
где d – внутренний диаметр, L – протяженность трубопровода, Q – расход нефти, соответственно. Вычисления провести в следующем порядке:
4). Функция если
если
если
В качестве исходных данных взять
Задание выполнить по вариантам:
6.3.2.Задача №2
Два прямолинейных участка дороги часто сопрягают по кривой, которая строится следующим образом: для первой половины кривой ее кривизна пропорциональна ее длине, вторая же половина кривой строится симметрично первой. Т.е. если величина S – длина участка кривой, отсчитываемая от ее начала, а K – кривизна кривой в конце этого участка, то Такие кривые называются клотоидами или спиралями Карно. Можно показать, что в прямоугольных координатах кривая задается следующим образом:
Эти интегралы носят название интегралов Френеля. Положим Вычисления интегралов предлагается провести по формуле трапеций. Данные по вариантам:
7. Методы решения задачи Коши для обыкновенных дифференциальных уравнений 1-го порядка 7.1. Основные понятия
Решение задачи Коши для уравнения вида Есть задачи, для которых решение можно найти аналитически. Но таких задач немного. А для остальных используют приближенные методы решения. Эти методы не дают аналитического вида функции, а значит и нельзя получить значение искомой функции в любой точке. Но они позволяют оценить приближенно значения искомой функции на некотором отрезке Для получения решения приближенными методами указанный отрезок Познакомимся с некоторыми из этих методов.
7.1.1. Метод Эйлера Этот простейший численный метод заключается в разложении искомой функции
Т.к.
Введя обозначение
Погрешность метода на каждом шаге вычислений имеет порядок
7.1.2. Модифицированный метод Эйлера
Этот метод имеет лучший порядок точности, и формулу для него получают, оставляя в разложении функции
Затем аппроксимируют вторую производную с помощью отношения конечных разностей:
Подставляя выражение (2) вместо второй производной в (1), получают:
И после преобразования:
Заменяя производные выражениями
где
Погрешность метода на каждом шаге вычислений имеет порядок
7.1.3. Метод Рунге-Кутта
Этот метод является самым популярным, т.к. дает хороший порядок точности. Формулу для этого метода получают, сохраняя в представлении функции Формулы метода Рунге-Кутта имеют следующий вид:
Погрешность метода на каждом шаге вычислений имеет порядок
Отметим некоторые существенные моменты применения указанных методов для решения обыкновенных дифференциальных уравнений первого порядка Заметим, что погрешность вычислений с каждым следующим шагом может иметь тенденцию к накоплению. Отсюда сразу следует, что лучше применять для расчетов методы, дающие более точный результат на каждой итерации. Из рассмотренных выше методов лучшим является метод Рунге-Кутта, ошибка в котором пропорциональна шагу в пятой степени. А так как шаг выбирается обычно маленьким, то и ошибка мала. Если метод решения выбран, то следующая задача – это выбор шага
7.1.4. Пример 1
Решим предлагаемую ниже задачу Коши методом Эйлера с заданным шагом на отрезке
Для данной задачи можно указать аналитическое выражение для функции решения. Легко проверить, что это будет функция Проведем расчеты по формуле Эйлера. По условию
Следовательно,
Выпишем полученные по методу Эйлера значения функции и значения точного решения в этих же точках в таблицу и проследим накопление ошибки:
7.1.5. Пример 2
Рассмотрим ту же задачу и решим ее теперь модифицированным методом Эйлера:
Формула метода имеет вид
Проведем по ней расчеты
Выпишем полученные по модифицированному методу Эйлера значения функции и значения точного решения в этих же точках в таблицу и проследим накопление ошибки:
Сравнивая картину погрешностей в этом методе и в методе Эйлера, можно видеть, что погрешности модифицированного метода Эйлера на порядок меньше соответствующих погрешностей метода Эйлера.
7.1.6. Пример 3
Решить ту же задачу методом Рунге-Кутта:
Запишем формулы метода Рунге-Кутта:
Проведем по ним расчеты. Для
Для
……………………………………………………………….. Для
Выпишем полученные по методу Рунге-Кутта значения функции и значения точного решения в этих же точках в таблицу и проследим накопление ошибки:
Сравнивая картину погрешностей в методе Рунге-Кутта и в рассмотренных ранее методе Эйлера и модифицированном методе Эйлера, можно видеть, что погрешности этого метода на несколько порядков меньше соответствующих погрешностей двух других методов. Именно поэтому метод Рунге-Кутта находит наибольшее применение.
7.2. Лабораторная работа №11 |
|
 Рассчитать потери напора при неизотермической перекачке нефти по участку трубопровода, равные
Рассчитать потери напора при неизотермической перекачке нефти по участку трубопровода, равные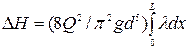
 начальная и конечная температуры соответственно,
начальная и конечная температуры соответственно, температура окружающей среды,
температура окружающей среды, кинематическая вязкость при температуре
кинематическая вязкость при температуре 
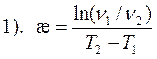
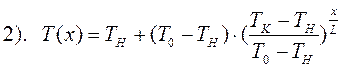
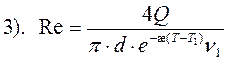
 зависит от величины числа Рейнольдса:
зависит от величины числа Рейнольдса: ламинарное течение , то
ламинарное течение , то ,
, переходный режим течения, то
переходный режим течения, то , где
, где ,
, течение в зоне гидравлически гладких труб, то
течение в зоне гидравлически гладких труб, то (Формула Блазиуса).
(Формула Блазиуса).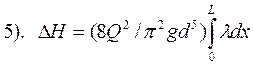
 и
и (
(  -сантистокс
-сантистокс




 .
.
 . Необходимо рассчитать координаты x, y точек сопрягающей кривой при различных S.
. Необходимо рассчитать координаты x, y точек сопрягающей кривой при различных S. заключается в отыскании функции
заключается в отыскании функции  , удовлетворяющей этому уравнению и начальному условию
, удовлетворяющей этому уравнению и начальному условию  .
. , где
, где  , а правый конец отрезка задан, исходя из потребностей.
, а правый конец отрезка задан, исходя из потребностей. , так что
, так что  . При этом говорят, что задается сетка. Шагом сетки h называется расстояние между соседними точками разбиения (узлами)
. При этом говорят, что задается сетка. Шагом сетки h называется расстояние между соседними точками разбиения (узлами)  . Оно равно
. Оно равно  . Значение функции
. Значение функции  известно: оно задается начальным условием
известно: оно задается начальным условием  в котором отбрасываются все члены, содержащие производные второго и более высоких порядков. Запишем это разложение в окрестности узла
в котором отбрасываются все члены, содержащие производные второго и более высоких порядков. Запишем это разложение в окрестности узла  :
: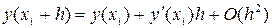
 и
и  , получаем:
, получаем: .
. , окончательно получаем формулу метода Эйлера, позволяющую по значению искомой функции
, окончательно получаем формулу метода Эйлера, позволяющую по значению искомой функции  в точке
в точке  найти значение ее
найти значение ее  в следующем узле
в следующем узле  :
: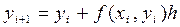 .
. . Это следует из того, что для получения формулы был отброшен член
. Это следует из того, что для получения формулы был отброшен член  . (1)
. (1) (2)
(2)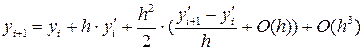 .
. (3)
(3) и
и  ,
, - найдено по формуле Эйлера, т.е.
- найдено по формуле Эйлера, т.е.  , получают формулу модифицированного метода Эйлера:
, получают формулу модифицированного метода Эйлера: , где
, где 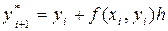
 . Это следует из того, что для получения формулы был отброшен член
. Это следует из того, что для получения формулы был отброшен член  .
. , где
, где 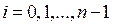
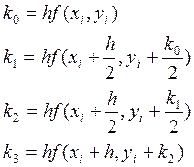
 .
. . И тут возникает следующая проблема. Допустим, нужно получить значения искомой функции на отрезке
. И тут возникает следующая проблема. Допустим, нужно получить значения искомой функции на отрезке  , где
, где  . С одной стороны, шаг нужно взять маленьким, чтобы ошибка каждого шага была небольшой. С другой стороны, при этом возрастет число шагов вычислений, что приводит в свою очередь к накоплению ошибки. Так что шаг в каждом случае следует выбирать некоторым оптимальным образом.
. С одной стороны, шаг нужно взять маленьким, чтобы ошибка каждого шага была небольшой. С другой стороны, при этом возрастет число шагов вычислений, что приводит в свою очередь к накоплению ошибки. Так что шаг в каждом случае следует выбирать некоторым оптимальным образом. :
: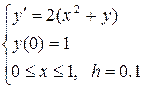
 . Здесь специально выбрана такого рода задача, чтобы иметь возможность сравнить работу методов, зная точные значения функции решения в точках разбиения отрезка
. Здесь специально выбрана такого рода задача, чтобы иметь возможность сравнить работу методов, зная точные значения функции решения в точках разбиения отрезка  . Формула Эйлера имеет вид:
. Формула Эйлера имеет вид:
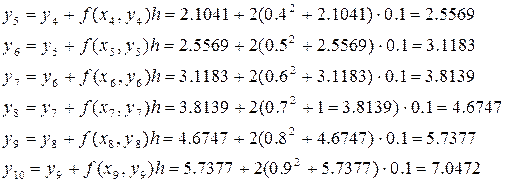







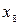


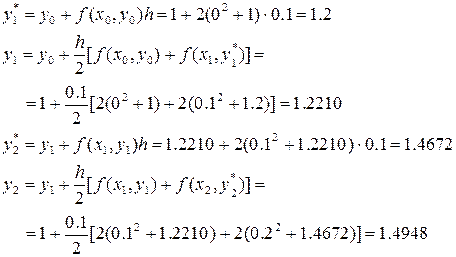
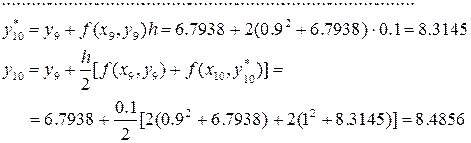
 , где
, где 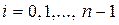
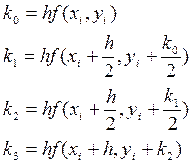
 имеем
имеем

 имеем
имеем
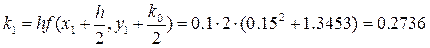
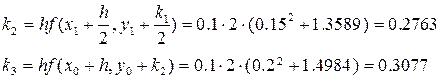
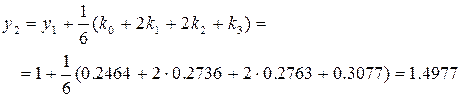
 имеем
имеем