|
|
Решение системы нелинейных уравнений методом Ньютона
Решить систему методом Ньютона, предварительно отделив корни графически:
5. Интерполяция и аппроксимация функции
5.1. Основные определения
Пусть величина y является функцией аргумента x, но вид аналитической зависимости 1). Построение функции 2). Построение функции
5.1.1. Интерполяция функции Имеются различные формулы для построения интерполяционного многочлена: формулы Лагранжа, Ньютона, Гаусса. Мы рассмотрим только интерполяционный многочлен Лагранжа. Он имеет вид:
Можно для лучшего понимания записать его в следующем виде: При этом легко заметить , что каждый многочлен
5.1.2. Аппроксимация функции
Для аппроксимации функции сначала необходимо выбрать степень аппроксимирующего многочлена, т.е. среди многочленов разной степени выбрать тот, который лучше отражает поведение заданной таблично функции. А затем с помощью метода наименьших квадратов определить параметры Для их поиска дифференцируют функционал S частным образом по
Продифференцируем S по параметрам:
…………………………………………………
Теперь, приравнивая эти производные нулю и перенося свободные константы в уравнениях
Решая эту систему линейных уравнений, находим значения параметров.
5.1.3. Пример 1 Построить интерполяционный многочлен Лагранжа для следующей заданной таблично функции
Если имеется пять значений функции в заданных точках, то интерполяционный многочлен мы получим четвертой степени, имеющим вид:
Сам интерполяционный многочлен имеет вид:
5.1.4. Пример 2
Найти с помощью метода наименьших квадратов аппроксимирующий многочлен для следующей таблично заданной функции
Т.к. исходная функция предполагается линейной, то в качестве аппроксимирующего многочлена выберем многочлен первой степени вида:
Тогда
где значения коэффициентов при неизвестных параметрах равны:
Получаем систему Следовательно, функция, аппроксимирующая заданную табличную функцию
5.1.5. Пример 3
Найти с помощью метода наименьших квадратов аппроксимирующий многочлен для той же таблично заданной функции, что и в предыдущем примере, но, приняв предположение, что зависимость
Т.к. исходная функция предполагается квадратичной, то в качестве аппроксимирующего многочлена выберем многочлен второй степени вида:
Тогда
где значения коэффициентов при неизвестных параметрах равны:
Система уравнений запишется в виде:
Решение этой системы методом Гаусса даст следующие значения параметров: Следовательно, аппроксимирующая функция имеет вид
5.2. Лабораторная работа № 7 |
|

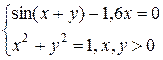






















 неизвестен, а имеется табличное задание этой функции в точках
неизвестен, а имеется табличное задание этой функции в точках  , т.е. значения
, т.е. значения  . Требуется построить функцию
. Требуется построить функцию  , которая мало отличалась бы от
, которая мало отличалась бы от  , и по которой можно было бы примерно оценить значения
, и по которой можно было бы примерно оценить значения  при
при  . Для решения такой проблемы используют два подхода:
. Для решения такой проблемы используют два подхода: , являющейся интерполяционным многочленом степени
, являющейся интерполяционным многочленом степени  и обладающей тем свойством, что значения ее в точках
и обладающей тем свойством, что значения ее в точках  , аппроксимирующей данную функцию f(x) и являющейся многочленом степени
, аппроксимирующей данную функцию f(x) и являющейся многочленом степени  вида
вида  , коэффициенты которого
, коэффициенты которого  определяются из условия минимизации суммы квадратов отклонений (метод наименьших квадратов) в точках
определяются из условия минимизации суммы квадратов отклонений (метод наименьших квадратов) в точках  от
от  соответственно, т.е. путем решения задачи:
соответственно, т.е. путем решения задачи:  . Рассмотрим оба подхода подробнее.
. Рассмотрим оба подхода подробнее. .
. , где
, где  .
. обладает тем свойством, что он обращается в ноль при всех табличных значениях аргумента
обладает тем свойством, что он обращается в ноль при всех табличных значениях аргумента  кроме
кроме  . А при
. А при  обладает необходимым свойством: его значения в точках
обладает необходимым свойством: его значения в точках  .
. . Тем самым получают систему линейных уравнений, содержащую
. Тем самым получают систему линейных уравнений, содержащую  но линейное уравнение, зависящее от
но линейное уравнение, зависящее от  .
.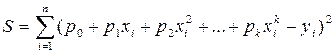
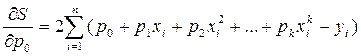
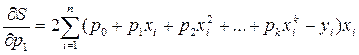
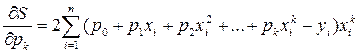
 в правую часть их, получим:
в правую часть их, получим: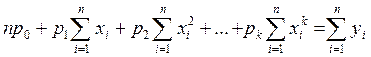
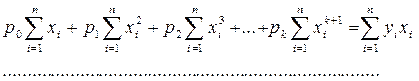
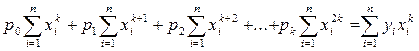
 , где
, где  сами являются так же многочленами четвертой степени от x. Вот как они получаются:
сами являются так же многочленами четвертой степени от x. Вот как они получаются: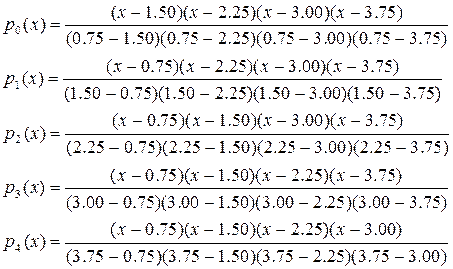
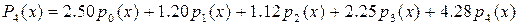
 .
. . Система линейных уравнений для поиска параметров
. Система линейных уравнений для поиска параметров  будет иметь следующий вид:
будет иметь следующий вид: ,
,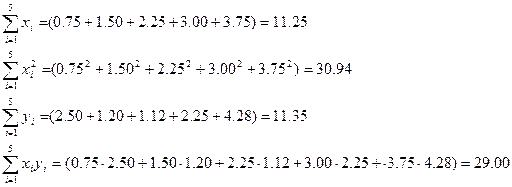
 , решая которую методом Гаусса получаем
, решая которую методом Гаусса получаем  .
. .
. .
. и система линейных уравнений для поиска параметров
и система линейных уравнений для поиска параметров  будет иметь следующий вид:
будет иметь следующий вид: ,
,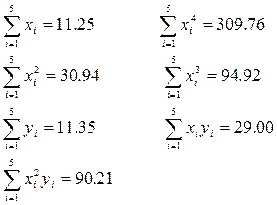
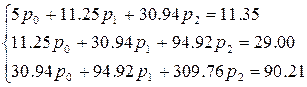
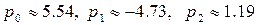 .
. .
.