|
|
Тема: Полное исследование функции. Построение графиковЦель: Формирование навыков исследования функции и построения графиков Время выполнения: 2 часа Требования к выполнению практической работы: 1.Ответить на теоретические вопросы. 2.Оформить задания в тетради для практических работ. Теоретический материал Общая схема построения графиков функций 1. Найдите область определения функции. 2. Выясните, не является ли функция четной, нечетной или периодической. 3. Найдите точки пересечения графика с осями координат (если это не вызывает затруднений). 4. Найдите асимптоты графика функции. 5. Найдите промежутки монотонности функции и ее экстремумы. 6. Найдите промежутки выпуклости графика функции и точки перегиба. 7. Постройте график, используя полученные результаты исследования. Пример Построить график функции Решение: 1. Функция определена на всей числовой оси, то есть 2. Данная функция не является ни четной, ни нечетной; кроме того, она не является периодической. 3. Найдем точку пересечения графика с осью 4. Очевидно, что график функции не имеет асимптот. 5. Найдем производную: 6. Найдем вторую производную: 7. Используя полученные данные, строим искомый график (рис. 1).
Задания для практической работы Исследуйте следующие функции и постройте их графики: 1) 3) 5) Вопросы для самоконтроля: 1. Дайте определение возрастания и убывания функции. 2. Дайте определение экстремума функции. 3. Как найти наибольшее и наименьшее значения функции? 4. Сформулируйте определение асимптоты. Перечислите основные виды асимптот. 5. Сформулируйте общую схему исследования функции для построения графика. Рекомендуемая литература: 1.1, 1.2, 1.3, 1.4, 1.5, 2.2, 2.3, 2.4, 2.5 Практическая работа №14 Тема: Интегрирование заменой переменной и по частям в неопределенном интеграле Цель: Формирование навыков нахождения неопределенных интегралов методами замены переменной и по частям Время выполнения: 2 часа Требования к выполнению практической работы: 1.Ответить на теоретические вопросы. 2.Оформить задания в тетради для практических работ. Теоретический материал Проинтегрировать функцию В основе интегрирования способом подстановки (или замены переменной) лежит свойство инвариантности формул интегрирования, которое заключается в следующем: если Замена переменной в неопределенном интеграле производится с помощью подстановок следующих двух типов: 1)
Функцию 2)
Интегрированием по частям называется нахождение интеграла по формуле
где При этом в качестве Так, при нахождении интегралов вида
за
за Примеры Найти интегралы: 1) Решение: 1) Данный интеграл окажется табличным, если под знаком дифференциала будет находиться аргумент 2) Предполагая
Задания для практической работы 1. Найдите интегралы методом непосредственного интегрирования: 1) 3) 5) 2. Найдите интегралы способом подстановки: 1) 3. Найдите интегралы при помощи интегрирования по частям: 1) Вопросы для самоконтроля: 1. Что называется первообразной? Перечислите свойства первообразной функции. 2. Что называется неопределенным интегралом? 3. Какие свойства неопределенного интеграла вы знаете? 4. Перечислите основные формулы интегрирования. 5. Какие методы интегрирования вы знаете? В чем заключается их сущность? Рекомендуемая литература: 1.1, 1.2, 1.3, 1.4, 1.5, 2.2, 2.3, 2.4, 2.5 Практическая работа №15 |
|
 .
. .
. : полагая
: полагая  , получим
, получим  . Точки пересечения графика с осью
. Точки пересечения графика с осью  в данном случае найти затруднительно.
в данном случае найти затруднительно. . Далее, имеем
. Далее, имеем 

 Точки
Точки  и
и 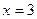 делят область определения функции на три промежутка:
делят область определения функции на три промежутка:  ,
,  и
и  . В промежутках
. В промежутках 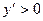 , то есть функция возрастает, а в промежутке
, то есть функция возрастает, а в промежутке  , то есть функция убывает. При переходе через точку
, то есть функция убывает. При переходе через точку 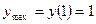 ,
, 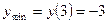 .
. ;
;  ,
,  . Точка
. Точка  и
и  . В первом из них
. В первом из них 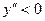 , а во втором
, а во втором 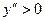 , то есть в промежутке
, то есть в промежутке  .
.
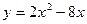 ; 2)
; 2) 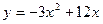 ;
; ; 4)
; 4) 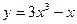 ;
; ; 6)
; 6)  .
.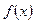 - значит найти ее неопределенный интеграл. Непосредственное интегрирование основано на прямом использовании основных свойств неопределенного интеграла и таблицы простейших интегралов.
- значит найти ее неопределенный интеграл. Непосредственное интегрирование основано на прямом использовании основных свойств неопределенного интеграла и таблицы простейших интегралов. , то
, то  , где
, где 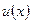 - произвольная дифференцируемая функция от
- произвольная дифференцируемая функция от 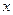 .
. - где
- где  - новая переменная, а
- новая переменная, а  - непрерывно дифференцируемая функция. В этом случае формула замены переменной такова:
- непрерывно дифференцируемая функция. В этом случае формула замены переменной такова: (14.1)
(14.1)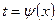 , где
, где  (14.2)
(14.2) , (14.3)
, (14.3) и
и  - непрерывно дифференцируемые функции от
- непрерывно дифференцируемые функции от  сводится к нахождению другого интеграла
сводится к нахождению другого интеграла 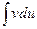 , ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.
, ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.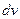 - та часть подынтегрального выражения, интеграл от которой известен или может быть найден.
- та часть подынтегрального выражения, интеграл от которой известен или может быть найден.
 , а за
, а за  ,
,  ; при отыскании интегралов вида
; при отыскании интегралов вида
 ,
,  ,
, 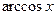 , а за
, а за  .
. ; 2)
; 2)  .
. подынтегральной функции
подынтегральной функции 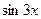 . Так как
. Так как  , то
, то 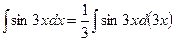 . Следовательно, подстановка
. Следовательно, подстановка  приводит рассматриваемый интеграл к табличному:
приводит рассматриваемый интеграл к табличному:  . Возвращаясь к старой переменной
. Возвращаясь к старой переменной  .
. ,
,  , найдем
, найдем  ,
,  . Следовательно,
. Следовательно, .
. ; 2)
; 2) 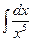 ;
; ; 4)
; 4) 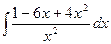 ;
; ; 6)
; 6)  .
. ; 2)
; 2) 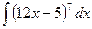 ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  ; 6)
; 6)  .
. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.