|
|
Обработка результатов прямых измерений
Обычно в реальных измерениях присутствуют и случайные и систематические (аппаратурные) погрешности. Если вычисленная случайная погрешность прямых измерений равна нулю или меньше аппаратурной в два и большее число раз, то при вычислении погрешности косвенных измерений в расчет должна приниматься аппаратурная погрешность. Если эти погрешности отличаются меньше, чем в два раза, то абсолютная погрешность вычисляется по формуле
Случайная погрешность измерения обычно неизвестна, как неизвестно и истинное значение измеряемой величины. Поэтому задача элементарной обработки результатов измерений заключается в установлении интервала, внутри которого с заданной вероятностью находится истинное значение измеряемой физической величины. Пусть в результате прямых измерений физической величины получен ряд ее значений: x1, x2, ..., xn. Зная этот ряд чисел, нужно указать значение, наиболее близкое к истинному значению измеряемой величины, и найти величину случайной погрешности. Эту задачу решают на основе теории вероятностей, подробное изложение которой выходит за рамки нашего курса. Наиболее вероятным значением измеряемой физической величины (близким к истинному) считают среднее арифметическое
Здесь xi - результат i-го измерения, n - число измерений. В случае малого n правильная оценка погрешности основана на использовании распределения Стьюдента (t – распределения). Случайная ошибка измерения может быть оценена величиной случайной абсолютной погрешности Dxсл., которую вычисляют по формуле
где t(a, n) - коэффициент Стьюдента, зависящий от числа измерений n и доверительной вероятности a. Значение доверительной вероятности a задает сам экспериментатор. Вероятностью случайного события называется отношение числа случаев, благоприятных для данного события, к общему числу равновозможных случаев. Вероятность достоверного события равна 1, а невозможного - 0. Значение коэффициента Стьюдента, соответствующее заданной доверительной вероятности a и определенному числу измерений n, находят по табл. 1. Из таблицы видно, что величина коэффициента Стьюдента и случайная погрешность измерения тем меньше, чем больше n и меньше a. Практически выбирают a = 0,95. Однако простое увеличение числа измерений не может свести общую погрешность к нулю, так как любой измерительный прибор дает погрешность. Таблица 1
Поясним смысл терминов абсолютная погрешность Dx и доверительная вероятность a, используя числовую ось. Пусть среднее значение измеряемой величины <x> (рис. 1), а вычисленная абсолютная погрешность Dx. Отложим Dx от <x> справа и слева. Полученный числовой интервал от (<x> ─ Δx) до (<x> + Dx) называется доверительным интервалом. Внутри этого доверительного интервала находится истинное значение измеряемой величины x.
Рис. 1
Если измерения той же величины повторить теми же приборами в тех же условиях, то истинное значение измеряемой величины xист. попадет в этот же доверительный интервал, но попадание будет не достоверным, а с вероятностью a. Вычислив величину абсолютной погрешности Dx по формуле (1), истинное значение x измеряемой физической величины можно записать в виде x = <x> ± Dx. Величина абсолютной погрешности Δx результата измерений еще не определяет точности измерений. Для оценки точности измерения физической величины подсчитывают относительную погрешность, которую обычно выражают в процентах:
За меру точности измерения принимают величину 1/ε. Следовательно, чем меньше относительная погрешность ε, тем выше точность измерений. Таким образом, при обработке результатов прямых измерений необходимо проделать следующее: 1. Провести измерения n раз (обычно 5). 2. Вычислить среднее арифметическое значение <x> по формуле (2). 3. Задать доверительную вероятность a (обычно берут a = 0,95). 4. По табл. 1 найти коэффициент Стьюдента, соответствующий заданной доверительной вероятности a и числу измерений n. 5. Вычислить абсолютную погрешность по формуле (3) и сравнить ее с аппаратурной погрешностью. Для дальнейших вычислений взять ту из них, которая больше (см. пример на с. 8). 6. По формуле (4) вычислить относительную ошибку e. 7. Записать окончательный результат
x = <x> ± Dx
с указанием относительной погрешности e и доверительной вероятности a. Обычно кроме прямых измерений в лабораторной работе присутствуют косвенные измерения.
|
|
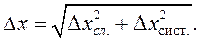 (1)
(1)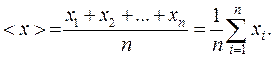 (2)
(2) (3)
(3)
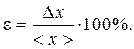 (4)
(4)