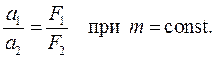|
|
Измерения и обработка результатов
В данной работе моделирование случайной величины осуществляется следующим образом. При помощи обычных часов с секундной стрелкой задают некоторый промежуток времени t и измеряют его высокочувствительным цифровым частотомером или электрическим секундомером, вручную нажимая кнопки "старт" и "стоп". Выполнять работу рекомендуется двум студентам. Первый многократно задает определенные промежутки времени по часам, подавая команду "старт" и "стоп". Второй нажимает кнопки и записывает отсчеты по прибору. В этом случае результаты измерений будут независимыми, что должно привести к нормальному (Гауссовому) распределению случайной величины. 1. Проведите 30-50 раз измерение выбранного промежутка времени. Можно задать промежуток времени от 5 до 10 секунд. Показания цифрового частотомера занесите во второй столбец табл. 1. 2. Найдите в табл. 1 наименьший tmin и наибольший tmax из результатов наблюдений. Промежуток (tmin - tmax) разбейте на 6 - 10 равных интервалов Δt. Границы интервалов занесите в табл. 2. 3. Подсчитайте число результатов наблюдений в табл. 2, попавших в каждый интервал Δti, и заполните второй столбец табл. 2. 4. Вычислите опытные значения плотности вероятности попадания случайной величины в каждый из интервалов Δti. Заполните третий столбец табл. 2. Таблица 1
5. Постройте гистограмму (рис. 1), для чего по оси абсцисс откладывайте интервалы Δti, являющиеся основаниями прямоугольников, высота которых равна плотности вероятности ρi.
Таблица 2
6. Вычислите <t> по (3) и s по (4). Можно воспользоваться результатами двадцати наблюдений. Полученные значения занесите в табл. 1. 7. По формуле (5) найдите максимальное значение плотности вероятности rmax при t = <t>. Результаты занести в табл. 1. Сравнить полученные значения rmax с наибольшей высотой гистограммы. 8. Для значений t, соответствующих границам выбранных интервалов, вычислите по функции Гаусса (1) значения плотности вероятности r(t) и занесите их в четвертый столбец табл. 2. 9. Нанесите все расчетные точки на график, на котором изображена гистограмма, и проведите через них плавную кривую. Сравните их. В чем причина неполного соответствия кривой Гаусса и гистограммы? 10. Проверьте, насколько точно выполняется в опытах соотношение (1). Вычислите границы интервалов, указанных в первом столбце табл. 3. По данным табл. 1 подсчитайте число наблюдений N12, попадающих в каждый из трех интервалов, а также отношение N12/N (6). Сравните их с известными значениями Р12, соответствующими нормальному распределению случайных величин (1). В чем причина небольшого расхождения?
Таблица 3
Контрольное задание
При обработке результатов измерения емкости для партии конденсаторов получено <C> = 1,1 мкФ, s = 0,1 мкФ. Если взять коробку со 100 конденсаторами из этой партии, то сколько среди них можно ожидать конденсаторов с ёмкостью меньше 1 мкФ? больше 1,3 мкФ? меньше 0,8 мкФ?
Контрольные вопросы
1. Что называется абсолютной, относительной, систематической и случайной погрешностями измерений? 2. Что такое средняя квадратичная погрешность, доверительный интервал и доверительная вероятность? 3. Какими свойствами обладает нормальное распределение результатов измерений? 4. Как найти случайную погрешность среднего значения из результатов эксперимента? 5. Как найти погрешность косвенных измерений? 6.Каков смысл введения коэффициентов Стьюдента? Как их определить. Библиографический список 1. Зайдель, А. Н. Ошибки измерений физических величин / А. Н. Зайдель. – СПб.: Лань, 2005. – с. 112.
ЛАБОРАТОРНАЯ РАБОТА № 2 ПРОВЕРКА ВТОРОГО ЗАКОНА НЬЮТОНА НА МАШИНЕ АТВУДА
Цель работы: проверка второго закона Ньютона. Оборудование: машина Атвуда с грузами и перегрузками, электрический секундомер.
Общие сведения
По второму закону Ньютона произведение массы частицы на ускорение равно действующей силе:
В общем случае результирующая сила является векторной суммой всех действующих на частицу сил:
Если на тело постоянной массы m действовать последовательно различными силами 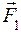 и и 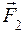 , тогда по второму закону Ньютона тело будет двигаться также с различными по величине ускорениями , тогда по второму закону Ньютона тело будет двигаться также с различными по величине ускорениями 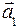 и и 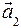 , отношение которых равно отношению сил: , отношение которых равно отношению сил:
С другой стороны, из уравнения (1) следует, что если на тела с различными массами m1 и m2 действуют равные силы 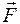 , то тела будут двигаться с разными по величине ускорениями , то тела будут двигаться с разными по величине ускорениями 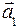 и и 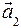 , отношение которых обратно отношению масс: , отношение которых обратно отношению масс:
|
|

 с-1
с-1
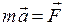 . (1)
. (1) . Выражение (1) называют также основным законом динамики поступательного движения. Оно справедливо не только для частицы, но и для тела, движущегося поступательно.
. Выражение (1) называют также основным законом динамики поступательного движения. Оно справедливо не только для частицы, но и для тела, движущегося поступательно.