|
|
Акон инерции. Инерциальные системы отсчета. Второй закон Ньютона. Третий закон Ньютона и область его применимости.Векторный и координатный способы описания движения точки в пространстве. Скорость (средняя, линейная, мгновенная) и ускорение. Вычисление пройденного пути и перемещения. 1) Координатный способ: Если с системой отсчета связать декартову систему координат (X, Y, Z) , то положение материальной точки А можно задать с помощью координат (x, y, z). Траекторию движения мы определим, если будем знать функцию x(t), y(t), z(t). 2) Векторый способ: В этом случае достаточно выбрать в системе отсчета точку О начала отсчета. Положение точки А будет определяться вектором
В механике вводится еще одна важная характеристика движения – ускорение, т.е. скорость изменения вектора скорости
Движение материальной точки по окружности (равномерное и произвольное). Баллистическое движение. Криволинейное движение точки в пространстве. Дв по окр это движ-е по траектории к-ая я-ся дугой окружности. При этом положение м/т м. определить углом пофорота φ и радиус вектора проведенного из центра окр в данную точку. Для описания вводится понятие угловой скорости x=Rcosφ y=Rsinφ,
Если угол поворота произвольным образом зависит от времени, то и
Скалярное произведение первого на второе равно нулю→ перпендикулярны
акон инерции. Инерциальные системы отсчета. Второй закон Ньютона. Третий закон Ньютона и область его применимости. Существуют с/сы отсчета названные инерциальными в зависимости к-х тела достаточно удалены д/д и движутся прямолинейно и равномерно В основе классической механики лежат три закона динамики, сформулированные Ньютоном в 1687г. Первый закон Ньютона: Всякое тело находится в состоянии покоя или равномерного и прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние. Первый закон Ньютона выполняется не во всякой системе отсчета. Система отсчета, в которой выполняется первый закон Ньютона, называется инерциальной системой отсчета. Инерциальных систем отсчета существует бесконечное множество. Любая система отсчета, движущаяся относительно некоторой инерциальной системы прямолинейно и равномерно (т.е. с постоянной скоростью), будет также инерциальной. Опытным путем установлено, что система отсчета, центр которой совмещен с Солнцем, а оси направлены на соответствующим образом выбранные звезды, являются инерциальной. Эта система называется гелиоцентрической системой отсчета. Всякое тело противится попыткам изменить его состояние движения. Это свойство тел называется инертностью. В качестве количественной характеристики инертности используется величина, называемая массой тела m. Для количественной характеристики взаимодействия тел или полей вводится физическая величина, называемая силой Второй закон Ньютона: Скорость изменения импульса тела равна геометрической сумме сил, действующих на данное тело: Третий закон Ньютона: Силы с которыми действуют друг на друга взаимодействующие тела, равны по величине и противоположны по направлению: При формулировке фундаментальных законов физики (в том числе и законов Ньютона) важно понимать, что эти законы (как и любые законы естествознания) имеют ограниченную область применимости. Так, законы классической механики применимы только для описания движения достаточно массивных макроскопических тел, при условии их движения с малыми (по сравнению со скоростью света) скоростями.
Сила упругости. Закон Гука Равновесному положению молекул в жидкости и твердом теле соответствует равенство сил притяжения и отталкивания. При деформации тел (как жидких, так и твердых) равновесные расстояния между молекулами изменяются, поэтому возникают силы, стремящиеся вернуть их в исходное состояние. Эти силы проявляются как силы упругости. Отметим, что силы упругости не относятся к фундаментальным, законы позволяющие вычислять их значения, как правило, являются экспериментальными и выполняются приближенно. В общем случае зависимость сил упругости от деформации может быть очень сложной, однако при малых деформации справедлив закон Р.Гука: сила упругости пропорциональна деформации тела и направлена в сторону противоположную деформации. В простейшем случае деформации растяжения и сжатия закон Р. Гука выражается формулой где x - изменение длины тела, k - коэффициент пропорциональности (так же называемый коэффициентом упругости), зависящий от материала тела, его размеров и формы. Знак минус явно указывает, что сила упругости направлена в сторону, противоположную деформации. Для того чтобы деформировать тело, к нему необходимо приложить внешнюю силу, тогда возникающие деформации приведут к появлению сил упругости (рис. 62). Итак, причиной деформаций являются внешние воздействия, а сами деформации являются причиной сил упругости. Если деформированное тело находится в состоянии равновесия, то возникающая сила упругости
6. Силы трения. проявлением межмолекулярных взаимодействий являются силы трения скольжения – силы, возникающие при относительном движении двух тел и направленные вдоль границы их соприкосновения. Одна из причин появления трения очевидна – поверхности взаимодействующих тел не являются идеально гладкими, микроскопические выступы и впадины зацепляются друг за друга, в них возникают силы упругости, направленные вдоль поверхности соприкосновения законы, описывающие рассматриваемый вид взаимодействия носят экспериментальный (эмпирический) характер. Наиболее простой вид закона, описывающего силу трения скольжения, установлен экспериментально и носит название закона Кулона-Амонтона. Это закон утверждает, что сила трения скольжения пропорциональна силе нормальной реакции взаимодействующих тел и направлена в сторону, противоположную скорости относительного движения тел (рис.68) Таким образом, сила трения покоя может принимать максимальное значение, после чего трение покоя переходит в терние скольжения. Силы, препятствующие движению, наблюдаются и при качении одного тела по поверхности другого. Эти силы называются силами трения качения. Сразу подчеркнем, что природа этих сил отличается от сил сухого трения. Основной причиной возникновения трения качения являются неупругие деформации самого катящегося тела и поверхности, по которой происходит качение. Так колесо, расположенное на горизонтальной поверхности деформирует последнюю. При движении колеса деформации не успевают восстановиться, поэтому колесу, приходится, как бы все время взбираться на небольшую горку, из-за чего появляется момент сил, тормозящий качение (рис. 72). Неупругие деформации колеса также приводят к появлению тормозящих сил. Таким образом, силы трения качения определяются упругими свойствами взаимодействующих тел. Закон для силы трения также является экспериментальным и приближенным, его принято записывать в форме где N - сила нормальной реакции, R - радиус катящегося тела, k - коэффициент трения качения, имеющий размерность длины. При записи формулы в такой форме, коэффициент трения качения определяется, главным образом, материалом взаимодействующих тел и не зависит от радиуса катящегося тела.
|
|
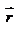 , проведенным из начала отсчета в данную точку А. Этот вектор называется радиус – вектором точки А. Траектория движения будет определяться функцией
, проведенным из начала отсчета в данную точку А. Этот вектор называется радиус – вектором точки А. Траектория движения будет определяться функцией 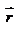 (t). Как мы видим векторный способ описания движения более экономный, поскольку требует определения одной функцией
(t). Как мы видим векторный способ описания движения более экономный, поскольку требует определения одной функцией 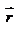 (t), правда, векторной функции от времени t.Для того, чтобы установить связь между этими двумя способами описания, введем три единичных вектора, орты
(t), правда, векторной функции от времени t.Для того, чтобы установить связь между этими двумя способами описания, введем три единичных вектора, орты  , направленных вдоль осей X, Y, Z, соответственно. Тогда, как видно из рисунка,
, направленных вдоль осей X, Y, Z, соответственно. Тогда, как видно из рисунка,  , а модуль радиус–вектора
, а модуль радиус–вектора  равен
равен 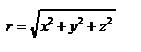 .
. Пусть материальная точка движется по траектории
Пусть материальная точка движется по траектории  (t), и пусть в момент времени t она находится в точке 1, описываемой радиус-вектором
(t), и пусть в момент времени t она находится в точке 1, описываемой радиус-вектором  . Рассмотрим достаточно близкий следующий момент времени t + Dt. В этот момент времени материальная точка находится в точке 2, и положение ее описывается радиус-вектором
. Рассмотрим достаточно близкий следующий момент времени t + Dt. В этот момент времени материальная точка находится в точке 2, и положение ее описывается радиус-вектором  . Тогда
. Тогда  , будет перемещение материальной точки за время Dt, а величина
, будет перемещение материальной точки за время Dt, а величина  будет представлять среднюю скорость точки на участке траектории 1®2. Мгновенную скорость
будет представлять среднюю скорость точки на участке траектории 1®2. Мгновенную скорость  определим как предел при t ® 0, т.е. как производную от радиус-вектора
определим как предел при t ® 0, т.е. как производную от радиус-вектора  .
.  - скорость при криволинейном движениии материальной точки. Как видно из рисунка скорость
- скорость при криволинейном движениии материальной точки. Как видно из рисунка скорость 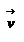 направлена по касательной к траектории. Далее при Dt®0 Dr® Ds, и линейная скорость v равен производной от пути по времени
направлена по касательной к траектории. Далее при Dt®0 Dr® Ds, и линейная скорость v равен производной от пути по времени  - модуль вектора скорости.
- модуль вектора скорости. во времени:
во времени:  - ускорение материальной точки. Учитывая определение скорости
- ускорение материальной точки. Учитывая определение скорости 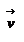 , ускорение
, ускорение 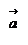 есть вторая производная от радиус-вектора
есть вторая производная от радиус-вектора  по времени t (две точки означают вторую производную по времени t).
по времени t (две точки означают вторую производную по времени t).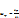 , мгновенная понимается как предел к к-му стремится
, мгновенная понимается как предел к к-му стремится  при стремлении к нулю
при стремлении к нулю  .
. 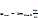 =
=  , при равномерном движении
, при равномерном движении  .
. →
→ .
.  →
→
 зависит от времени.
зависит от времени.  угловое ускорение есть предел к которому стремится отношение Δω к Δt→0
угловое ускорение есть предел к которому стремится отношение Δω к Δt→0 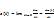 ,
, 

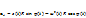

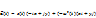

 Воздействие на данное тело со стороны других тел вызывает изменение его скорости. Опыт показывает, что одинаковые воздействия на разные тела, вызывают разные по величине изменения скоростей этих тел. Чтобы описать этот опытный факт, вводится понятие импульса тела или количества движения:
Воздействие на данное тело со стороны других тел вызывает изменение его скорости. Опыт показывает, что одинаковые воздействия на разные тела, вызывают разные по величине изменения скоростей этих тел. Чтобы описать этот опытный факт, вводится понятие импульса тела или количества движения:  .
. . Подставляя сюда выражение для импульса тела
. Подставляя сюда выражение для импульса тела 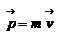 , получим еще одну формулировку второго закона Ньютона: Произведение массы тела на его ускорение равно геометрической сумме сил, действующих на тела
, получим еще одну формулировку второго закона Ньютона: Произведение массы тела на его ускорение равно геометрической сумме сил, действующих на тела  - второй закон Ньютона. Всякое действие тел друг на друга носит характер взаимодействия: если тело 1 действует на тело 2 с силой
- второй закон Ньютона. Всякое действие тел друг на друга носит характер взаимодействия: если тело 1 действует на тело 2 с силой  , то и тело 2 в свою очередь действует на тело 1 с силой
, то и тело 2 в свою очередь действует на тело 1 с силой  .
.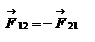 - третий закон Ньютона. Эти силы не компенсируют друг друга, поскольку приложены к разным телам.
- третий закон Ньютона. Эти силы не компенсируют друг друга, поскольку приложены к разным телам. , (1)
, (1) оказывается равной по величине и противоположной по направлению внешней силе
оказывается равной по величине и противоположной по направлению внешней силе  . Таким образом, соотношение
. Таким образом, соотношение 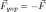 справедливо только в состоянии равновесия и является следствием условий равновесия, а не 3 закона Ньютона.
справедливо только в состоянии равновесия и является следствием условий равновесия, а не 3 закона Ньютона. , (1) безразмерный коэффициент пропорциональности (называемый коэффициент трения) μ зависит от материала соприкасающихся поверхностей и степени их обработки. Как правило, этот коэффициент определяется экспериментально. Сила трения может возникнуть и в том случае, когда тела не движутся друг относительно друга, такую силу называют силой трения покоя. Повседневный опыт указывает, что для того чтобы сдвинуть одно тело относительно другого, необходимо приложить силу, превышающую определенное пороговое значение
, (1) безразмерный коэффициент пропорциональности (называемый коэффициент трения) μ зависит от материала соприкасающихся поверхностей и степени их обработки. Как правило, этот коэффициент определяется экспериментально. Сила трения может возникнуть и в том случае, когда тела не движутся друг относительно друга, такую силу называют силой трения покоя. Повседневный опыт указывает, что для того чтобы сдвинуть одно тело относительно другого, необходимо приложить силу, превышающую определенное пороговое значение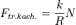 , (2)
, (2)