Обратная связь
|
Кинетическая энергия материальной точки. Связь кинетической энергии с работой сил. Теорема Кенига. Кинетическая энергия(или энергия движения) определяется массами и скоростями рассматриваемых тел. Рассмотрим материальную точку, движущуюся под действием силы 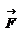 . Работа этой силы увеличивает кинетическую энергию материальной точки . Работа этой силы увеличивает кинетическую энергию материальной точки  . Вычислим в этом случае малое приращение (дифференциал) кинетической энергии: . Вычислим в этом случае малое приращение (дифференциал) кинетической энергии: 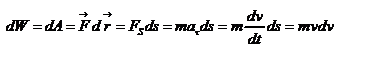 . При вычислении . При вычислении  использован второй закон Ньютона использован второй закон Ньютона 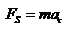 , а также , а также 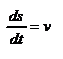 - модуль скорости материальной точки. Тогда - модуль скорости материальной точки. Тогда 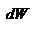 можно представить в виде: можно представить в виде: 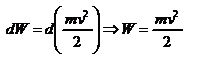 -- кинетическая энергия движущейся материальной точки. -- кинетическая энергия движущейся материальной точки.
Теперь рассмотрим связь кинетической энергии с работой. Если постоянная сила действует на тело, то оно будет двигаться в направлении силы. Тогда элементарная работа по перемещению тела из точки 1 в точку 2, будет равна произведению силы F на перемещение dr : dA = F dr, отсюда 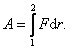 , , 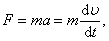  , , 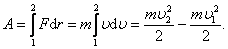 . Окончательно получаем: . Окончательно получаем: 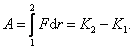 . Следовательно, работа силы, приложенной к телу на пути r, численно равна изменению кинетической энергии этого тела: . Следовательно, работа силы, приложенной к телу на пути r, численно равна изменению кинетической энергии этого тела: 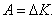 Или изменение кинетической энергии dK равно работе внешних сил: dK=dA. Или изменение кинетической энергии dK равно работе внешних сил: dK=dA.
Рассмотрим 2 с/сы отсчета S и S’,   Кинетическую энергию тела относительно ИСО найдем, исходя из определения: Eк=Smivi2/2=Smi(Vc+vi')2/2=SmiVc2/2+ Smivi'2/2+SmiVcvi'. Кинетическую энергию тела относительно ИСО найдем, исходя из определения: Eк=Smivi2/2=Smi(Vc+vi')2/2=SmiVc2/2+ Smivi'2/2+SmiVcvi'.
Полученное выражение представляет собой сумму трех слагаемых: 
Кинетическая энергия твердого тела состоит из кинетической энергии его поступательного движения и энергии его движения E' относительно СО, связанной с центром масс. Это утверждение называется теоремой Кёнига. Eк = E' + M·Vc2/2. Для точки обода 
12. Потенциальная энергия в поле центральных сил (потенциальное поле, консервативные силы). Закон сохранения механической энергии. Силы, работа которых на замкнутом пути равна нулю, называетсяконсервативными.
Потенциальная энергия (или энергия положения тел) определяется действием на тело консервативных сил и зависит только от положения тела. Мы видели, что работу силы тяжести 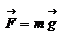 при криволинейном движении материальной точки при криволинейном движении материальной точки 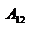 можно представить в виде разности значений функции можно представить в виде разности значений функции 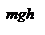 , взятых в точке 1 и в точке 2: , взятых в точке 1 и в точке 2:  . Оказывается, что всегда, когда силы консервативны, работу этих сил на пути 1 . Оказывается, что всегда, когда силы консервативны, работу этих сил на пути 1  2 можно представить в виде: 2 можно представить в виде: 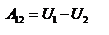 . Функция . Функция  , которая зависит только от положения тела – называется потенциальной энергией. , которая зависит только от положения тела – называется потенциальной энергией. 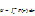 – выражение для нахождения потенциальной энергии в случае центральных сил взаимодействия когда точки находятся на расстоянии r д/д. Тогда для элементарной работы получим – выражение для нахождения потенциальной энергии в случае центральных сил взаимодействия когда точки находятся на расстоянии r д/д. Тогда для элементарной работы получим 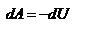 – работа равна убыли потенциальной энергии. Иначе можно сказать, что работа совершается за счёт запаса потенциальной энергии. Величину – работа равна убыли потенциальной энергии. Иначе можно сказать, что работа совершается за счёт запаса потенциальной энергии. Величину 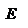 , равную сумме кинетической и потенциальной энергий частицы, называют полной механической энергией тела: , равную сумме кинетической и потенциальной энергий частицы, называют полной механической энергией тела: 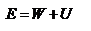 – полная механическая энергия тела. В заключении заметим, что используя второй закон Ньютона – полная механическая энергия тела. В заключении заметим, что используя второй закон Ньютона 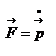 , дифференциал кинетической энергии , дифференциал кинетической энергии 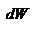 можно представить в виде: можно представить в виде: 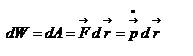 . Дифференциал потенциальной энергии . Дифференциал потенциальной энергии 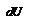 , как указывали выше, равен: , как указывали выше, равен: 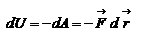 . Таким образом, если сила . Таким образом, если сила  – консервативная сила и отсутствуют другие внешние силы, то – консервативная сила и отсутствуют другие внешние силы, то 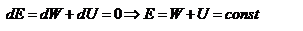 , т.е. в этом случае полная механическая энергия тела сохраняется. , т.е. в этом случае полная механическая энергия тела сохраняется.
Закон сохранения механической энергии системы материальных точек. Рассмотрим систему, состоящую из n материальных точек, между которыми действуют консервативные силы внутреннего взаимодействия 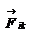 , и кроме того на материальные точки действуют внешние консервативные силы , и кроме того на материальные точки действуют внешние консервативные силы 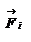 и внешние неконсервативные силы и внешние неконсервативные силы 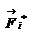 . Для каждой материальной точки запишем второй закон Ньютона: . Для каждой материальной точки запишем второй закон Ньютона:  , , 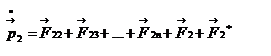 ,…, ,…, 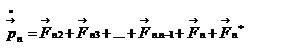 . Далее левые и правые части каждого уравнения умножим скалярно на . Далее левые и правые части каждого уравнения умножим скалярно на 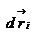 , соответственно, где , соответственно, где 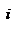 – номер материальной точки. Покажем это на примере – номер материальной точки. Покажем это на примере 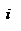 -ой материальной точки: -ой материальной точки: 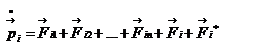 ½ ½  , , 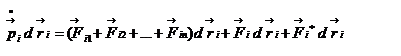 . Это равенство можно записать в виде: . Это равенство можно записать в виде: 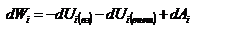 , или , или  , где , где 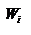 – кинетическая энергия – кинетическая энергия  -ой материальной точки, -ой материальной точки, 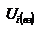 – внутренняя потенциальная энергия – внутренняя потенциальная энергия  -ой материальной точки, -ой материальной точки, 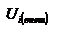 – внешняя потенциальная энергия – внешняя потенциальная энергия  -ой материальной точки, -ой материальной точки, 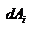 – работа, которую совершают над – работа, которую совершают над 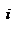 -ой материальной точкой внешняя неконсервативная сила. Просуммируем левые и правые части преобразованных указанным образом уравнений движения. -ой материальной точкой внешняя неконсервативная сила. Просуммируем левые и правые части преобразованных указанным образом уравнений движения. 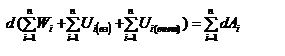 , или , или  , где , где  – кинетическая энергия системы материальных точек, – кинетическая энергия системы материальных точек, 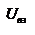 , ,  – внутренняя и внешняя потенциальная энергия м.т., – внутренняя и внешняя потенциальная энергия м.т., 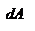 – полная работа внешних неконсервативных сил. Если внешние неконсервативные силы отсутствуют, правая часть полученного уравнения будет равна нулю и, следовательно, полная механическая энергия системы остается постоянной: – полная работа внешних неконсервативных сил. Если внешние неконсервативные силы отсутствуют, правая часть полученного уравнения будет равна нулю и, следовательно, полная механическая энергия системы остается постоянной: 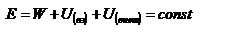 –- закон сохранения механической энергии системы материальных точек. Полная механическая энергия системы материальных точек, на которые действуют лишь консервативные силы, остается постоянной, т.е. сохраняется во времени. Для замкнутой системы закон сохранения полной механической энергии имеет вид: –- закон сохранения механической энергии системы материальных точек. Полная механическая энергия системы материальных точек, на которые действуют лишь консервативные силы, остается постоянной, т.е. сохраняется во времени. Для замкнутой системы закон сохранения полной механической энергии имеет вид: 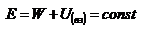 . Полная механическая энергия замкнутой системы материальных точек, между которыми действуют только консервативные силы, остается постоянной, т.е. сохраняется во времени. Если в замкнутой системе, кроме консервативных, действуют такие неконсервативные силы, например, силы трения, то полная механическая энергия системы не сохраняется. . Полная механическая энергия замкнутой системы материальных точек, между которыми действуют только консервативные силы, остается постоянной, т.е. сохраняется во времени. Если в замкнутой системе, кроме консервативных, действуют такие неконсервативные силы, например, силы трения, то полная механическая энергия системы не сохраняется.
13. Понятие момента силы и момента импульса, связь между ними. Закон динамики вращательного движения (для материальной точки и системы материальных точек). Закон сохранения момента импульса.
Для простоты рассмотрим случай плоского движения, т.е. траектория движения материальной точки лежит в одной плоскости, которую мы расположим перпендикулярно плоскости листа. Выберем на плоскости начало координат О и положение материальной точки будем описывать радиус-вектором 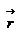 . Скорость точки . Скорость точки 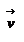 , ее импульс , ее импульс 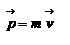 , ускорение , ускорение 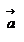 , и сила , и сила 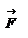 будут расположены в плоски движения материальной точки, как показано на рисунке. будут расположены в плоски движения материальной точки, как показано на рисунке.
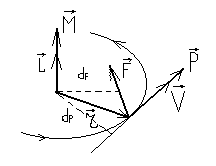 Введем две новые физические величины: момент силы Введем две новые физические величины: момент силы 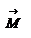 и момент импульса и момент импульса 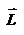 относительно начала координат O. относительно начала координат O. 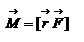 -- момент силы относительно начала координат. Модуль вектора -- момент силы относительно начала координат. Модуль вектора 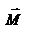 равен равен 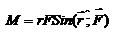 , где , где 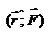 - угол между векторами - угол между векторами 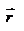 и и 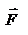 . Если опустить перпендикуляр из точки O на направление действия силы, то его длина . Если опустить перпендикуляр из точки O на направление действия силы, то его длина 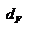 будет плечом силы будет плечом силы 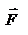 , ,  и модуль момента сил будет равен произведению силы на плечо, т.е. и модуль момента сил будет равен произведению силы на плечо, т.е. 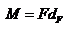 , что совпадает со школьным определением момента силы. Аналогично моменту силы вводится момент импульса , что совпадает со школьным определением момента силы. Аналогично моменту силы вводится момент импульса 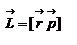 - момент импульса материальной точки относительно начала координат. - момент импульса материальной точки относительно начала координат. 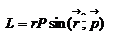 , где , где 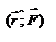 - угол между векторами - угол между векторами 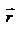 и и 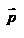 , ,  —плечо импульса —плечо импульса  , т.е. длина перпендикуляра, опущенного из точки O на направление вектора , т.е. длина перпендикуляра, опущенного из точки O на направление вектора 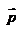 материальной точки. Оба вектора материальной точки. Оба вектора 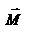 и и 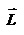 , согласно определения направлены перпендикулярно плоскости движения материальной точки. В общем случае неплоского движения, направление векторов , согласно определения направлены перпендикулярно плоскости движения материальной точки. В общем случае неплоского движения, направление векторов 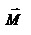 и и 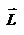 не совпадают, но существует закон, который связывает момент импульса не совпадают, но существует закон, который связывает момент импульса 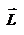 с моментом силы с моментом силы 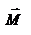 . Чтобы установить этот закон, возьмем производную от вектора . Чтобы установить этот закон, возьмем производную от вектора 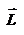 : :  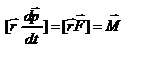 .В результате получаем: .В результате получаем: 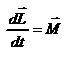 -- закон изменения момента импульса материальной точки относительно начала координат. -- закон изменения момента импульса материальной точки относительно начала координат.
|
|
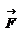 . Работа этой силы увеличивает кинетическую энергию материальной точки
. Работа этой силы увеличивает кинетическую энергию материальной точки  . Вычислим в этом случае малое приращение (дифференциал) кинетической энергии:
. Вычислим в этом случае малое приращение (дифференциал) кинетической энергии: 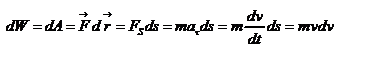 . При вычислении
. При вычислении  использован второй закон Ньютона
использован второй закон Ньютона 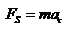 , а также
, а также 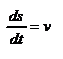 - модуль скорости материальной точки. Тогда
- модуль скорости материальной точки. Тогда 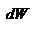 можно представить в виде:
можно представить в виде: 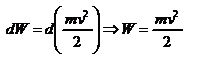 -- кинетическая энергия движущейся материальной точки.
-- кинетическая энергия движущейся материальной точки.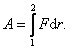 ,
, 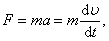
 ,
, 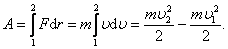 . Окончательно получаем:
. Окончательно получаем: 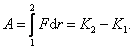 . Следовательно, работа силы, приложенной к телу на пути r, численно равна изменению кинетической энергии этого тела:
. Следовательно, работа силы, приложенной к телу на пути r, численно равна изменению кинетической энергии этого тела: 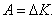 Или изменение кинетической энергии dK равно работе внешних сил: dK=dA.
Или изменение кинетической энергии dK равно работе внешних сил: dK=dA.
 Кинетическую энергию тела относительно ИСО найдем, исходя из определения: Eк=Smivi2/2=Smi(Vc+vi')2/2=SmiVc2/2+ Smivi'2/2+SmiVcvi'.
Кинетическую энергию тела относительно ИСО найдем, исходя из определения: Eк=Smivi2/2=Smi(Vc+vi')2/2=SmiVc2/2+ Smivi'2/2+SmiVcvi'.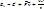

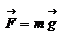 при криволинейном движении материальной точки
при криволинейном движении материальной точки 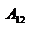 можно представить в виде разности значений функции
можно представить в виде разности значений функции 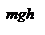 , взятых в точке 1 и в точке 2:
, взятых в точке 1 и в точке 2:  . Оказывается, что всегда, когда силы консервативны, работу этих сил на пути 1
. Оказывается, что всегда, когда силы консервативны, работу этих сил на пути 1 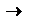 2 можно представить в виде:
2 можно представить в виде: 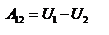 . Функция
. Функция  , которая зависит только от положения тела – называется потенциальной энергией.
, которая зависит только от положения тела – называется потенциальной энергией. 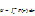 – выражение для нахождения потенциальной энергии в случае центральных сил взаимодействия когда точки находятся на расстоянии r д/д. Тогда для элементарной работы получим
– выражение для нахождения потенциальной энергии в случае центральных сил взаимодействия когда точки находятся на расстоянии r д/д. Тогда для элементарной работы получим 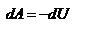 – работа равна убыли потенциальной энергии. Иначе можно сказать, что работа совершается за счёт запаса потенциальной энергии. Величину
– работа равна убыли потенциальной энергии. Иначе можно сказать, что работа совершается за счёт запаса потенциальной энергии. Величину 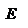 , равную сумме кинетической и потенциальной энергий частицы, называют полной механической энергией тела:
, равную сумме кинетической и потенциальной энергий частицы, называют полной механической энергией тела: 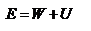 – полная механическая энергия тела. В заключении заметим, что используя второй закон Ньютона
– полная механическая энергия тела. В заключении заметим, что используя второй закон Ньютона 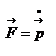 , дифференциал кинетической энергии
, дифференциал кинетической энергии 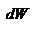 можно представить в виде:
можно представить в виде: 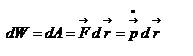 . Дифференциал потенциальной энергии
. Дифференциал потенциальной энергии 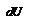 , как указывали выше, равен:
, как указывали выше, равен: 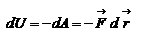 . Таким образом, если сила
. Таким образом, если сила 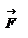 – консервативная сила и отсутствуют другие внешние силы, то
– консервативная сила и отсутствуют другие внешние силы, то 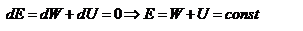 , т.е. в этом случае полная механическая энергия тела сохраняется.
, т.е. в этом случае полная механическая энергия тела сохраняется.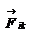 , и кроме того на материальные точки действуют внешние консервативные силы
, и кроме того на материальные точки действуют внешние консервативные силы 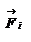 и внешние неконсервативные силы
и внешние неконсервативные силы 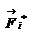 . Для каждой материальной точки запишем второй закон Ньютона:
. Для каждой материальной точки запишем второй закон Ньютона:  ,
, 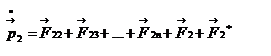 ,…,
,…, 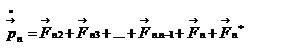 . Далее левые и правые части каждого уравнения умножим скалярно на
. Далее левые и правые части каждого уравнения умножим скалярно на 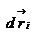 , соответственно, где
, соответственно, где 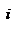 – номер материальной точки. Покажем это на примере
– номер материальной точки. Покажем это на примере 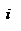 -ой материальной точки:
-ой материальной точки: 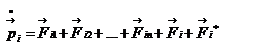 ½
½  ,
, 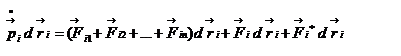 . Это равенство можно записать в виде:
. Это равенство можно записать в виде: 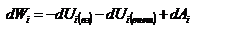 , или
, или  , где
, где 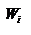 – кинетическая энергия
– кинетическая энергия  -ой материальной точки,
-ой материальной точки, 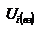 – внутренняя потенциальная энергия
– внутренняя потенциальная энергия 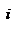 -ой материальной точки,
-ой материальной точки,  – внешняя потенциальная энергия
– внешняя потенциальная энергия 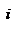 -ой материальной точки,
-ой материальной точки,  – работа, которую совершают над
– работа, которую совершают над 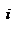 -ой материальной точкой внешняя неконсервативная сила. Просуммируем левые и правые части преобразованных указанным образом уравнений движения.
-ой материальной точкой внешняя неконсервативная сила. Просуммируем левые и правые части преобразованных указанным образом уравнений движения. 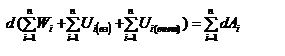 , или
, или  , где
, где  – кинетическая энергия системы материальных точек,
– кинетическая энергия системы материальных точек, 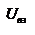 ,
,  – внутренняя и внешняя потенциальная энергия м.т.,
– внутренняя и внешняя потенциальная энергия м.т., 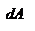 – полная работа внешних неконсервативных сил. Если внешние неконсервативные силы отсутствуют, правая часть полученного уравнения будет равна нулю и, следовательно, полная механическая энергия системы остается постоянной:
– полная работа внешних неконсервативных сил. Если внешние неконсервативные силы отсутствуют, правая часть полученного уравнения будет равна нулю и, следовательно, полная механическая энергия системы остается постоянной: 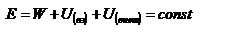 –- закон сохранения механической энергии системы материальных точек. Полная механическая энергия системы материальных точек, на которые действуют лишь консервативные силы, остается постоянной, т.е. сохраняется во времени. Для замкнутой системы закон сохранения полной механической энергии имеет вид:
–- закон сохранения механической энергии системы материальных точек. Полная механическая энергия системы материальных точек, на которые действуют лишь консервативные силы, остается постоянной, т.е. сохраняется во времени. Для замкнутой системы закон сохранения полной механической энергии имеет вид: 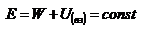 . Полная механическая энергия замкнутой системы материальных точек, между которыми действуют только консервативные силы, остается постоянной, т.е. сохраняется во времени. Если в замкнутой системе, кроме консервативных, действуют такие неконсервативные силы, например, силы трения, то полная механическая энергия системы не сохраняется.
. Полная механическая энергия замкнутой системы материальных точек, между которыми действуют только консервативные силы, остается постоянной, т.е. сохраняется во времени. Если в замкнутой системе, кроме консервативных, действуют такие неконсервативные силы, например, силы трения, то полная механическая энергия системы не сохраняется.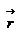 . Скорость точки
. Скорость точки 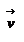 , ее импульс
, ее импульс 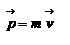 , ускорение
, ускорение 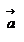 , и сила
, и сила 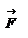 будут расположены в плоски движения материальной точки, как показано на рисунке.
будут расположены в плоски движения материальной точки, как показано на рисунке. Введем две новые физические величины: момент силы
Введем две новые физические величины: момент силы 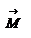 и момент импульса
и момент импульса 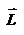 относительно начала координат O.
относительно начала координат O. 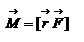 -- момент силы относительно начала координат. Модуль вектора
-- момент силы относительно начала координат. Модуль вектора 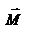 равен
равен 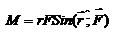 , где
, где 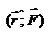 - угол между векторами
- угол между векторами 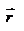 и
и 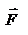 . Если опустить перпендикуляр из точки O на направление действия силы, то его длина
. Если опустить перпендикуляр из точки O на направление действия силы, то его длина 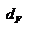 будет плечом силы
будет плечом силы 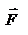 ,
,  и модуль момента сил будет равен произведению силы на плечо, т.е.
и модуль момента сил будет равен произведению силы на плечо, т.е. 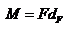 , что совпадает со школьным определением момента силы. Аналогично моменту силы вводится момент импульса
, что совпадает со школьным определением момента силы. Аналогично моменту силы вводится момент импульса 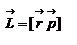 - момент импульса материальной точки относительно начала координат.
- момент импульса материальной точки относительно начала координат. 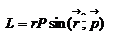 , где
, где 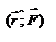 - угол между векторами
- угол между векторами 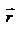 и
и 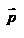 ,
,  —плечо импульса
—плечо импульса  , т.е. длина перпендикуляра, опущенного из точки O на направление вектора
, т.е. длина перпендикуляра, опущенного из точки O на направление вектора 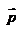 материальной точки. Оба вектора
материальной точки. Оба вектора 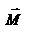 и
и 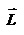 , согласно определения направлены перпендикулярно плоскости движения материальной точки. В общем случае неплоского движения, направление векторов
, согласно определения направлены перпендикулярно плоскости движения материальной точки. В общем случае неплоского движения, направление векторов 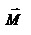 и
и 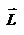 не совпадают, но существует закон, который связывает момент импульса
не совпадают, но существует закон, который связывает момент импульса 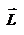 с моментом силы
с моментом силы 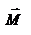 . Чтобы установить этот закон, возьмем производную от вектора
. Чтобы установить этот закон, возьмем производную от вектора 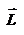 :
: 
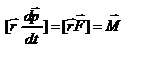 .В результате получаем:
.В результате получаем: 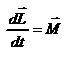 -- закон изменения момента импульса материальной точки относительно начала координат.
-- закон изменения момента импульса материальной точки относительно начала координат.