Обратная связь
|
Параметры, определяющие состояние вещества. Идеальный газ. Вывод основного уравнения кинетической теории газов. Вывод основных газовых законов. Уравнение состояния идеальных газов. Идеальным газом называется газ, молекулы которого не взаимодействуют друг с другом на расстоянии и имеют исчезающе малые собственные размеры. Состояние заданной массы m идеального газа определяется значениями трёх параметров: давления P, объёма V, и температуры Т.
Уравнение состояния идеального газа или уравнение Менделеева - Клапейрона является обобщением законов идеального газа, открытых экспериментально до создания МКТ. Однако, из основного уравнения МКТ (2.3), можно получить уравнение состояния идеального газа. Для этого подставим вместо средней кинетической энергии поступательного движения молекулы в основное уравнение МКТ идеальных газов правую часть равенства (2.4), получим уравнение, в которое не входят микропараметры газа  (2.5). Так как (2.5). Так как  , следовательно, , следовательно,  или или  . Учитывая, что . Учитывая, что  , получим N=NA , получим N=NA  , а так как NA×k = R = 8,3 , а так как NA×k = R = 8,3  - молярная газовая постоянная[2,3,5,15] или универсальная газовая постоянная [1,6,7,] , то получим уравнение Менделеева - молярная газовая постоянная[2,3,5,15] или универсальная газовая постоянная [1,6,7,] , то получим уравнение Менделеева  (2.6). Уравнение состояния газа часто удобно использовать в записи, предложенной Клапейроном, если количество вещества не изменяется (2.6). Уравнение состояния газа часто удобно использовать в записи, предложенной Клапейроном, если количество вещества не изменяется  или или  (2.7). Уравнение (2.7) часто называют обобщённым газовым законом. Тот факт, что из основного уравнения молекулярно-кинетической теории идеального газа можно вывести уравнение состояния идеального газа, подтверждает верность молекулярно-кинетической теории вещества. (2.7). Уравнение (2.7) часто называют обобщённым газовым законом. Тот факт, что из основного уравнения молекулярно-кинетической теории идеального газа можно вывести уравнение состояния идеального газа, подтверждает верность молекулярно-кинетической теории вещества.
Основное уравнение молекулярно – кинетической теории газов. Возьмем сосуд с газом и определим давление P газа на стенки сосуда. Для простоты рассмотрения выберем этот сосуд в форме куба с ребром l и расположим его в декартовой системе координат, как показано на рисунке. Пусть в сосуде имеется всего N молекул. Предположим, что:
1)Вдоль оси х движется одна треть всех молекул, т.е.  ; ;
2)Удар молекул о стенку Q идеально упругий и молекулы проходят расстояние, равное размеру куба, не испытывая соударений.
 Импульс силы, полученный стенкой при ударе молекулы, определим из второго закона Ньютона. Импульс силы, полученный стенкой при ударе молекулы, определим из второго закона Ньютона.  . где . где  - изменение импульса молекулы, m – масса молекулы. Поскольку масса стенки намного больше массы молекулы, то - изменение импульса молекулы, m – масса молекулы. Поскольку масса стенки намного больше массы молекулы, то  и и  или по модулю или по модулю  , где использовано обозначение , где использовано обозначение  . Таким образом, одна молекула одна молекула за время Dt передает стенке импульс силы . Таким образом, одна молекула одна молекула за время Dt передает стенке импульс силы  , а за время , а за время  сек передаёт стенке импульс силы равный сек передаёт стенке импульс силы равный  , где k – число ударов молекул за 1 сек. , где k – число ударов молекул за 1 сек.  Так как Так как  - промежуток времени между двумя последовательными ударами,. то - промежуток времени между двумя последовательными ударами,. то  , тогда , тогда  . Теперь подсчитаем суммарный импульс силы, который передают стенке N1 молекул, движущихся вдоль оси x, за 1 сек . Теперь подсчитаем суммарный импульс силы, который передают стенке N1 молекул, движущихся вдоль оси x, за 1 сек  , где скобки < > обозначают среднее значение выражения, стоящего в скобках. Если извлечь корень квадратный из < V2 >, получим среднюю квадратичную скорость молекул, которую будем обозначать <Vкв> , где скобки < > обозначают среднее значение выражения, стоящего в скобках. Если извлечь корень квадратный из < V2 >, получим среднюю квадратичную скорость молекул, которую будем обозначать <Vкв>  - средняя квадратичная скорость молекул газа. Давление, оказываемое газом на грань куба, равно: - средняя квадратичная скорость молекул газа. Давление, оказываемое газом на грань куба, равно:  , где n – концентрация молекул. Запишем это выражение в виде , где n – концентрация молекул. Запишем это выражение в виде  , чтобы подчеркнуть, что в левую часть этого выражения входит средняя кинетическая энергия поступательного движения молекулы , чтобы подчеркнуть, что в левую часть этого выражения входит средняя кинетическая энергия поступательного движения молекулы  . Тогда . Тогда  - основное уравнение молекулярно-кинетической теории ( уравнение Клаузиуса ) С учетом уравнения состояния идеального газа: - основное уравнение молекулярно-кинетической теории ( уравнение Клаузиуса ) С учетом уравнения состояния идеального газа:  получаем выражение для средней кинетической энергии поступательного движения молекул: получаем выражение для средней кинетической энергии поступательного движения молекул:  - средняя кинетическая энергия поступательного движения молекул. Мы видим, что величина kT есть мера энергии теплового движения молекул. - средняя кинетическая энергия поступательного движения молекул. Мы видим, что величина kT есть мера энергии теплового движения молекул.
Газовые законы установлены в 17 веке экспериментально. Однако, их можно получить, используя уравнение Менделеева - Клапейрона.
Закон Бойля-Мариотта.Для данногоколичества вещества 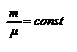 рассмотрим изотермический процесс, то есть процесс, протекающий без изменения температуры (Т= const). Используя уравнение (2.6) или (2.7), получим уравнение изотермы, выраженное через давление и объём газа: рассмотрим изотермический процесс, то есть процесс, протекающий без изменения температуры (Т= const). Используя уравнение (2.6) или (2.7), получим уравнение изотермы, выраженное через давление и объём газа:  (2.7). или (2.7). или  (2.7’). Для данного количества вещества при изотермическом процессе произведение давления на объём есть величина постоянная. Для построения диаграммы Р(V) выразим давление через объем (2.7’). Для данного количества вещества при изотермическом процессе произведение давления на объём есть величина постоянная. Для построения диаграммы Р(V) выразим давление через объем  . Зависимость между давлением и объёмом – обратно пропорциональная, графически представлена гиперболой на рис.2.3 а. Температурные зависимости давления и объёма представлены на рис.2.3 б и в, соответственно. . Зависимость между давлением и объёмом – обратно пропорциональная, графически представлена гиперболой на рис.2.3 а. Температурные зависимости давления и объёма представлены на рис.2.3 б и в, соответственно.
Закон Гей-Люссака.Для данного количества вещества  рассмотрим изобарический процесс, то есть процесс, протекающий без изменения давления рассмотрим изобарический процесс, то есть процесс, протекающий без изменения давления
(Р = const). Используя уравнение (2.6) или (2.7), получим уравнениеизобары, выраженное через температуру и объём:  ,(2.8). через параметры начального и конечного состояния ,(2.8). через параметры начального и конечного состояния  или или  . Для данного количества вещества при изобарическом процессе отношение объёма к температуре (или наоборот) есть постоянная величина. Изобарический закон можно записать и в виде: . Для данного количества вещества при изобарическом процессе отношение объёма к температуре (или наоборот) есть постоянная величина. Изобарический закон можно записать и в виде:  . Здесь V0 - объём газа при t=00C, t- температура в 0С, a - термический коэффициент объемного расширения; . Здесь V0 - объём газа при t=00C, t- температура в 0С, a - термический коэффициент объемного расширения;  . Для идеального газа . Для идеального газа  , ,  , но , но  , тогда , тогда  - термический коэффициент объёмного расширения идеального газа равен величине, обратной температуры. Изображение этого процесса приведено на рис. 2.4. Закон Шарля. Для данного количества вещества - термический коэффициент объёмного расширения идеального газа равен величине, обратной температуры. Изображение этого процесса приведено на рис. 2.4. Закон Шарля. Для данного количества вещества  рассмотрим изохорический процесс, то есть процесс, протекающий без изменения объёма (V = const). Используя уравнение (2.6) или (2.7), получим уравнениеизохоры, выраженное через температуру и давление газа: рассмотрим изохорический процесс, то есть процесс, протекающий без изменения объёма (V = const). Используя уравнение (2.6) или (2.7), получим уравнениеизохоры, выраженное через температуру и давление газа:  , (2.9) через параметры начального и конечного состояния , (2.9) через параметры начального и конечного состояния  или или 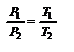 . Для данного количества вещества при изохорическом процессе отношение давления к температуре (или наоборот) есть величина постоянная. . Для данного количества вещества при изохорическом процессе отношение давления к температуре (или наоборот) есть величина постоянная.
Изображение этого процесса приведено на рис. 2.5.
Закон АвогадроПри одинаковых давлениях (Р) и температурах (Т) в равных объемах (V) любого газа содержится одинаковое число молекул.   , следовательно, N1 = N2 , следовательно, N1 = N2
Закон Дальтона(для смеси газов) Давление смеси газов равно сумме парциальных давлений Рсм=Р1+Р2+... +РК (2.10). Этот закон можно также получить, используя уравнение состояния идеального газа.  , ,   - парциальное давление - давление, которое оказывал бы данный компонент газа, если бы он один занимал весь объем, предоставленный смеси. - парциальное давление - давление, которое оказывал бы данный компонент газа, если бы он один занимал весь объем, предоставленный смеси.
|
|
 (2.5). Так как
(2.5). Так как  , следовательно,
, следовательно,  или
или  . Учитывая, что
. Учитывая, что  , получим N=NA
, получим N=NA  , а так как NA×k = R = 8,3
, а так как NA×k = R = 8,3  - молярная газовая постоянная[2,3,5,15] или универсальная газовая постоянная [1,6,7,] , то получим уравнение Менделеева
- молярная газовая постоянная[2,3,5,15] или универсальная газовая постоянная [1,6,7,] , то получим уравнение Менделеева  (2.6). Уравнение состояния газа часто удобно использовать в записи, предложенной Клапейроном, если количество вещества не изменяется
(2.6). Уравнение состояния газа часто удобно использовать в записи, предложенной Клапейроном, если количество вещества не изменяется  или
или  (2.7). Уравнение (2.7) часто называют обобщённым газовым законом. Тот факт, что из основного уравнения молекулярно-кинетической теории идеального газа можно вывести уравнение состояния идеального газа, подтверждает верность молекулярно-кинетической теории вещества.
(2.7). Уравнение (2.7) часто называют обобщённым газовым законом. Тот факт, что из основного уравнения молекулярно-кинетической теории идеального газа можно вывести уравнение состояния идеального газа, подтверждает верность молекулярно-кинетической теории вещества. ;
; Импульс силы, полученный стенкой при ударе молекулы, определим из второго закона Ньютона.
Импульс силы, полученный стенкой при ударе молекулы, определим из второго закона Ньютона.  . где
. где  - изменение импульса молекулы, m – масса молекулы. Поскольку масса стенки намного больше массы молекулы, то
- изменение импульса молекулы, m – масса молекулы. Поскольку масса стенки намного больше массы молекулы, то  и
и  или по модулю
или по модулю  , где использовано обозначение
, где использовано обозначение  . Таким образом, одна молекула одна молекула за время Dt передает стенке импульс силы
. Таким образом, одна молекула одна молекула за время Dt передает стенке импульс силы  , а за время
, а за время  сек передаёт стенке импульс силы равный
сек передаёт стенке импульс силы равный  , где k – число ударов молекул за 1 сек.
, где k – число ударов молекул за 1 сек.  Так как
Так как  - промежуток времени между двумя последовательными ударами,. то
- промежуток времени между двумя последовательными ударами,. то  , тогда
, тогда  . Теперь подсчитаем суммарный импульс силы, который передают стенке N1 молекул, движущихся вдоль оси x, за 1 сек
. Теперь подсчитаем суммарный импульс силы, который передают стенке N1 молекул, движущихся вдоль оси x, за 1 сек  , где скобки < > обозначают среднее значение выражения, стоящего в скобках. Если извлечь корень квадратный из < V2 >, получим среднюю квадратичную скорость молекул, которую будем обозначать <Vкв>
, где скобки < > обозначают среднее значение выражения, стоящего в скобках. Если извлечь корень квадратный из < V2 >, получим среднюю квадратичную скорость молекул, которую будем обозначать <Vкв>  - средняя квадратичная скорость молекул газа. Давление, оказываемое газом на грань куба, равно:
- средняя квадратичная скорость молекул газа. Давление, оказываемое газом на грань куба, равно:  , где n – концентрация молекул. Запишем это выражение в виде
, где n – концентрация молекул. Запишем это выражение в виде  , чтобы подчеркнуть, что в левую часть этого выражения входит средняя кинетическая энергия поступательного движения молекулы
, чтобы подчеркнуть, что в левую часть этого выражения входит средняя кинетическая энергия поступательного движения молекулы  . Тогда
. Тогда  - основное уравнение молекулярно-кинетической теории ( уравнение Клаузиуса ) С учетом уравнения состояния идеального газа:
- основное уравнение молекулярно-кинетической теории ( уравнение Клаузиуса ) С учетом уравнения состояния идеального газа:  получаем выражение для средней кинетической энергии поступательного движения молекул:
получаем выражение для средней кинетической энергии поступательного движения молекул:  - средняя кинетическая энергия поступательного движения молекул. Мы видим, что величина kT есть мера энергии теплового движения молекул.
- средняя кинетическая энергия поступательного движения молекул. Мы видим, что величина kT есть мера энергии теплового движения молекул.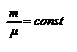 рассмотрим изотермический процесс, то есть процесс, протекающий без изменения температуры (Т= const). Используя уравнение (2.6) или (2.7), получим уравнение изотермы, выраженное через давление и объём газа:
рассмотрим изотермический процесс, то есть процесс, протекающий без изменения температуры (Т= const). Используя уравнение (2.6) или (2.7), получим уравнение изотермы, выраженное через давление и объём газа:  (2.7). или
(2.7). или  (2.7’). Для данного количества вещества при изотермическом процессе произведение давления на объём есть величина постоянная. Для построения диаграммы Р(V) выразим давление через объем
(2.7’). Для данного количества вещества при изотермическом процессе произведение давления на объём есть величина постоянная. Для построения диаграммы Р(V) выразим давление через объем  . Зависимость между давлением и объёмом – обратно пропорциональная, графически представлена гиперболой на рис.2.3 а. Температурные зависимости давления и объёма представлены на рис.2.3 б и в, соответственно.
. Зависимость между давлением и объёмом – обратно пропорциональная, графически представлена гиперболой на рис.2.3 а. Температурные зависимости давления и объёма представлены на рис.2.3 б и в, соответственно. рассмотрим изобарический процесс, то есть процесс, протекающий без изменения давления
рассмотрим изобарический процесс, то есть процесс, протекающий без изменения давления ,(2.8). через параметры начального и конечного состояния
,(2.8). через параметры начального и конечного состояния  или
или  . Для данного количества вещества при изобарическом процессе отношение объёма к температуре (или наоборот) есть постоянная величина. Изобарический закон можно записать и в виде:
. Для данного количества вещества при изобарическом процессе отношение объёма к температуре (или наоборот) есть постоянная величина. Изобарический закон можно записать и в виде:  . Здесь V0 - объём газа при t=00C, t- температура в 0С, a - термический коэффициент объемного расширения;
. Здесь V0 - объём газа при t=00C, t- температура в 0С, a - термический коэффициент объемного расширения;  . Для идеального газа
. Для идеального газа  ,
,  , но
, но  , тогда
, тогда  - термический коэффициент объёмного расширения идеального газа равен величине, обратной температуры. Изображение этого процесса приведено на рис. 2.4. Закон Шарля. Для данного количества вещества
- термический коэффициент объёмного расширения идеального газа равен величине, обратной температуры. Изображение этого процесса приведено на рис. 2.4. Закон Шарля. Для данного количества вещества  рассмотрим изохорический процесс, то есть процесс, протекающий без изменения объёма (V = const). Используя уравнение (2.6) или (2.7), получим уравнениеизохоры, выраженное через температуру и давление газа:
рассмотрим изохорический процесс, то есть процесс, протекающий без изменения объёма (V = const). Используя уравнение (2.6) или (2.7), получим уравнениеизохоры, выраженное через температуру и давление газа:  , (2.9) через параметры начального и конечного состояния
, (2.9) через параметры начального и конечного состояния  или
или 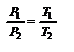 . Для данного количества вещества при изохорическом процессе отношение давления к температуре (или наоборот) есть величина постоянная.
. Для данного количества вещества при изохорическом процессе отношение давления к температуре (или наоборот) есть величина постоянная.
 , следовательно, N1 = N2
, следовательно, N1 = N2 ,
, 
 - парциальное давление - давление, которое оказывал бы данный компонент газа, если бы он один занимал весь объем, предоставленный смеси.
- парциальное давление - давление, которое оказывал бы данный компонент газа, если бы он один занимал весь объем, предоставленный смеси.