|
|
Свойства эмпирических статистических совокупностей. Графическое изображение распределенияМетодические рекомендации к выполнению Лабораторных работ
Издательство Национального исследовательского Иркутского государственного технического университета
Физика. Молекулярная физика: методические рекомендации к выполнению лабораторных работ. / Сост.: А.Д. Афанасьев, Л.В. Днепровская, М.Я. Яраева Иркутск: Изд-во ИрГТУ, 2011. 92с.
Соответствует содержанию разделов государственных стандартов по направлениям 090900 Информационная безопасность, 210400 Радиотехника, 222900 Наноматериалы и микросистемная техника, 210700 Инфокоммуникационные технологии и системы связи. Содержат описания 8 лабораторных работ по курсу физики (раздел «Молекулярная физика»). Предназначены для студентов 1 курса специальностям 090900 Информационная безопасность, 210400 Радиотехника, 222900 Наноматериалы и микросистемная техника, 210700 Инфокоммуникационные технологии и системы связи Физико-технического института Национального исследовательского Иркутского государственного технического университета
Библиогр. назв., иллюстр. 42, табл. 17
Лабораторная работа 2-1 Изучение статистического распределения частоты электрических сигналов Цель работы: Ознакомиться со статистическими закономерностями физических величин Задача работы: Провести статистическое исследование эмпирической совокупности частоты электрических сигналов, регистрируемых от сети пересчетным прибором. Теоретическая часть Экспериментальное распределение В природе, в жизни, в технике часто встречаются случайные явления. Предсказать отдельные случайные явления нельзя, так как на них сказывается влияние очень большого числа неподдающихся контролю факторов. Например, при стрельбе в цель, при измерениях физических величин, в движении молекул, и азартных играх и т. п. в той или иной степени наблюдаются элементы случайности. Однако даже если можно было бы учесть все определяющие данное явление факторы, то одно единичное явление еще не характеризует общей картины случайных явлений. Например, одно наугад выбранное отверстие в мишени почти ничего не говорит нам о меткости стрелка, в то время как большое число произведенных выстрелов дает понятие о точности стрельбы в цель. Случайные явления наиболее полно описываются при помощи математического аппарата теории вероятности. Большая совокупность случайных явлений или величин подчиняется так называемым статистическим законам. Статистические законы дают возможность определять вероятность, с которой осуществляется то или иное событие в серии случайных однотипных событий, средние величины в серии измеряемых величин, наиболее вероятные отклонения от среднего и т. п. Все эти характеристики определяются законом распределения случайных величин - зависимостью вероятности появления данной величины от значения самой величины. Случайное событие, случайная величина Основой для построения статистических моделей служит теория вероятностей. Предметом этой теории является изучение случайных событий и случайных величин. Событие называется случайным, если при данных условиях оно может произойти или не произойти. Случайная величина – это переменная, принимающая в результате испытаний то или иное числовое значение в зависимости от случайного исхода испытания. Случайная величина может рассматриваться как функция, аргументом которой служит элементарное случайное событие поля испытаний. Можно выделить два основных типа случайных величин: дискретные и непрерывные. Дискретной случайной величиной называется такая случайная величина, которая может принимать конечное или бесконечное счетное множество значений, элементы которого могут быть занумерованы в каком-нибудь порядке и выписаны в последовательности. В качестве примера дискретных величин, которые могут принимать целочисленные значения, можно указать число дефектных изделий в какой-либо партии, число вызовов, поступающих на телефонную станцию в часы наибольшей нагрузки, число частиц в геологической пробе и т. д. Непрерывной случайной величиной называется такая величина, которая может принимать любые значения в любых интервалах, находящихся в указанных участках. К величинам такого характера относятся погрешности измерений, координаты молекул газа в сосуде, шумы в радиоприемных устройствах и т.п. Свойства эмпирических статистических совокупностей. Графическое изображение распределения Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего объекты. Если совокупность содержит большое число объектов, то в случайном порядке отбирают из всей совокупности ограниченное число объектов и подвергают их изучению. Выборочной совокупностью или просто выборной называют совокупность случайно отобранных объектов. Совокупность объектов, из которых производится выборка, называется генеральной. Совокупность случайных величин, обладающих качественной общностью, называется статистической совокупностью, а каждый член этой совокупности вариантой. Число вариант в совокупности представляет объём совокупности. Статистическая совокупность может состоять из непрерывно меняющихся или дискретных случайных величин. Для того чтобы по данным выборки можно было достаточно уверенно судить об интересующем признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли. Иначе говоря, выборка должна быть репрезентативной (представительной). К первой задаче статистической обработки относится группировка вариант в совокупности. Группировка является одним из важнейших положений статистической теории. Метод группировок определяется задачами исследования и является основой математической статистики. Рассмотрим один из способов группировок, заключающийся в распределении числа случайных величин по значениям дискретной случайной величины или по интервалам непрерывной случайной величины. Рассмотрим данный способ группировки на примере статистической совокупности, представляющей собой золотосодержащую пробу, в которую попало 100 золотых частичек разного диаметра. Диаметр частичек является непрерывной случайной величиной xi : x1, x2, x3, ….. xi, x100 Совокупность вариант-диаметров записывается в виде 10 столбцов по 10 вариант в каждом в той последовательности, в какой значения диаметра были получены в результате эксперимента. Затем определяется размах изменения вариант совокупности
Полученный размах (1) совокупности делится на определенное число интервалов К, которое определяется объемом совокупности N
Ширина каждого интервала
должна способствовать выявлению основных черт распределения случайных величин и сглаживанию случайных колебаний. Поэтому экспериментатор может отступать от указанного числа интервалов (2-1.2) и брать большее или меньшее число интервалов в зависимости от поставленных задач эксперимента и объема совокупности. При этом нужно помнить, что ширина интервала не должна быть меньше цены деления измерительного прибора. Если деление (2-1.3) не выполняется нацело, то результат округляют обычно в большую сторону, чтобы не потерять часть полученных результатов. Для нахождения числа вариант в каждом интервале необходимо определить границы всех интервалов. За верхнюю границу первого интервала нужно взять xmax. Следующие границы всех интервалов распределяются таким образом:
При совпадении границ интервалов с вариантой последнюю вносят в интервал по совпадению с верхней границей интервала. Число вариант, попавших в интервал, называется частотой ni (
Распределение частоты по значениям случайной дискретной величины или по интервалам непрерывной случайной величины называется законом распределения. |
|
 .
.
 .
.
 .
.
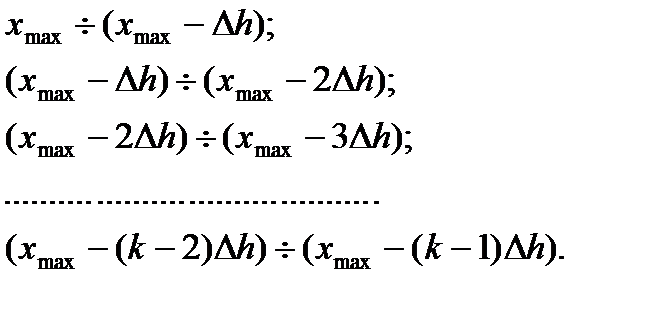
 ), а отношение частоты к объему совокупности – относительной частотой или частостью vi:
), а отношение частоты к объему совокупности – относительной частотой или частостью vi:
 .
.