|
|
Параметрические критерии различияПараметрические критерии позволяют установить совпадение или различие между параметрами двух распределений – их средними значениями, дисперсиями, коэффициентами асимметрии, эксцесса и т. д. При пользовании параметрическими критериями обычно предполагается, что сравниваемые распределения в общем однотипны и могут отличаться лишь значениями своих параметров. Из-за случайности в образовании выборки распределения вариант в выборке всегда отличаются от их распределения в генеральной совокупности; поэтому если в генеральной совокупности варианты распределены по определенному теоретическому закону, то распределение в выборке будет заведомо отклоняться от этого закона. Отсюда следует, что сам факт отклонения выборочного распределения от того или иного теоретического распределения еще не дает основания утверждать, что и в генеральной совокупности распределение не подчиняется данному теоретическому закону. Таким образом, вопрос сводится к тому, можно ли расхождение между выборочным и предположенным теоретическим распределением отнести за счет расхождения между выборкой и генеральной совокупностью, или же оно является результатом того, что сама генеральная совокупность отклоняется от данного теоретического распределения В любом случае задача может быть сведена к проверке гипотезы об отсутствии реального различия. Эту гипотезу называют нулевой гипотезой. Предельно допустимое значение вероятности, начиная с которого вероятность можно считать малой, называют уровнем значимости. Если вероятность нулевой гипотезы a < 1% , то она отвергается, если вероятность лежит в пределах от 1% до 5%, то возможность отвергнуть нулевую гипотезу сомнительна, если же Критерий соответствия К. Пирсон предложил критерий
где Чтобы дать правило проверки, следует выбрать уровень значимости для критерия. Определив значение
Экспериментальная часть Задача работы: Статистическое исследование эмпирической совокупности частоты электрических сигналов, регистрируемых от сети пересчетным прибором. Приборы и принадлежности 1. Пересчетный прибор ПС-02-08 (или ПП-16). 2. Секундомер. Порядок выполнения работы 1. Ознакомиться с инструкцией работы пересчетного прибора. 2. Получить статистическую совокупность вариант частоты электрических сигналов за время 10 секунд. Объем совокупности N = 100. 3. Провести обсчет полученных результатов с помощью программы Excel. Для этого занести в Excel данные и построить таблицу 2-2.1. Провести группировку полученной статистической совокупности от меньшего к большему, найти Таблица 2-2.1
3. Рассчитать частоту n и частость nвыпадения вариант. Результаты вычислений занести в таблицу 2-2.2. Построить гистограмму и полигон экспериментального распределения на миллиметровке. Таблица 2-2.2
4. Графически сравнить экспериментальное распределение с распределением Гаусса при экспериментально полученных значениях Для этого определить значение плотности вероятности экспериментального распределения предполагая, что оно подчиняется закону Гаусса и f(x) определится по формуле
где xi – среднее по интервалу, Таблица 2-2.3
5. Построить график совместимости ni (полигон) и график f(x)Dh. Используя формулу (2-1.29) для c2 – критерия, определить его значение и сопоставить с критическим, установить принадлежность экспериментального распределения нормальному.
Контрольные вопросы 1. Что такое случайное событие, случайная величина, дискретная случайная величина, непрерывная случайная величина? 2. Что такое варианта, статистическая совокупность, частота, частость, закон распределения? 3. Что такое гистограмма, полигон? Какими свойствами они обладают? 4. Назовите основные параметры экспериментального распределения. 5. Что такое теоретическое распределение, каковы его параметры? 6. Каков смысл дифференциальной и интегральной функций нормального распределения? Как они выражаются на графике дифференциальной функции? 7. Какова связь между параметрами генеральной и выборочной совокупности? 8. Каков смысл параметрических критериев? 9. В чем заключается смысл c-критерия? Список литературы 1. Кассандрова О.Н., Лебедев В.В. Обработка результатов наблюдений. М. : Наука, 1970. 2. Гмурман В.Е. Теория вероятностей и математическая статистика : учеб. пособие для вузов. М. : Высш.шк., 2004. 479с. 3. Гусак А.А. Высшая математика т.2 : учебник для студентов вузов. Мн. : ТетраСистем, 2001. 448с. 4. Физический практикум / Под ред. В.И. Ивероновой. М. : Гос. изд-во физико-математической литературы, 1962. 956с. Лабораторная работа 2-2 |
|
 , то нулевая гипотеза принимается. Выбор уровня значимости определяется в различных случаях конкретными задачами исследования.
, то нулевая гипотеза принимается. Выбор уровня значимости определяется в различных случаях конкретными задачами исследования.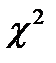
 (хи-квадрат) для оценки степени различия двух сравниваемых рядов частостей (можно сравнивать эмпирический и теоретический или два эмпирических распределения). Этот критерий представляет собой сумму отношений квадратов разностей между частостями эмпирического и теоретического распределений к частостям (вероятностям) теоретического распределения:
(хи-квадрат) для оценки степени различия двух сравниваемых рядов частостей (можно сравнивать эмпирический и теоретический или два эмпирических распределения). Этот критерий представляет собой сумму отношений квадратов разностей между частостями эмпирического и теоретического распределений к частостям (вероятностям) теоретического распределения: , (2-1.29)
, (2-1.29)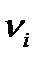 – частость эмпирического распределения,
– частость эмпирического распределения, 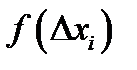 – вероятность теоретического распределения.
– вероятность теоретического распределения. , соответствующим выбранному уровню значимости. Если
, соответствующим выбранному уровню значимости. Если  , то расхождение между экспериментальным и теоретическим распределением несущественно, и экспериментальное распределение можно аппроксимировать теоретическим.
, то расхождение между экспериментальным и теоретическим распределением несущественно, и экспериментальное распределение можно аппроксимировать теоретическим.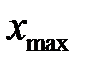 и
и  , Dx определить, выбрать число интервалов К, найти ширину интервала Dh, определить границы интервала. Определить отклонения вариант от среднего значения, квадраты этих отклонений, их кубы и четвертые степени. Рассчитать
, Dx определить, выбрать число интервалов К, найти ширину интервала Dh, определить границы интервала. Определить отклонения вариант от среднего значения, квадраты этих отклонений, их кубы и четвертые степени. Рассчитать  - среднее по всем значениям, S – среднее квадратичное, доверительный интервал
- среднее по всем значениям, S – среднее квадратичное, доверительный интервал  (используя коэффициенты Стьюдента
(используя коэффициенты Стьюдента  , где g - доверительная вероятность равная 0,95), асимметрию и эксцесс. Сделать вывод о принадлежности экспериментального распределения к нормальному.
, где g - доверительная вероятность равная 0,95), асимметрию и эксцесс. Сделать вывод о принадлежности экспериментального распределения к нормальному.
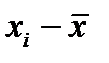




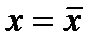 ±
± 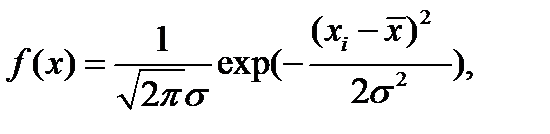 (2-1.30)
(2-1.30)