|
|
Описание экспериментальной установкиБаллон с распределительным краном, U- образный манометр, насос секундомер. Схема установки предоставлена на рис. 2-6.1. Установка состоит из стеклянного баллона Б, который может быть соединен с помощью распределительного крана К либо c атмосферой, либо с насосом Н и манометром М. Водяной U -образный манометр измеряет разность между давлением в баллоне и атмосферным давлением в мм. водного столба.
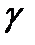 для газа, находящегося в баллоне, с ним проводят последовательность термодинамических процессов, представленных на для газа, находящегося в баллоне, с ним проводят последовательность термодинамических процессов, представленных на  - диаграммерис. 2-6.2.Обозначим через - диаграммерис. 2-6.2.Обозначим через  исходные величины термодинамических параметров газа в баллоне. Сначала в баллон накачивается воздух (процесс 1-2). При этом газ в баллоне сжимается и нагревается. После изохорического остывания до начальной комнатной температуры исходные величины термодинамических параметров газа в баллоне. Сначала в баллон накачивается воздух (процесс 1-2). При этом газ в баллоне сжимается и нагревается. После изохорического остывания до начальной комнатной температуры 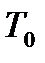 газ имеет некоторое давление газ имеет некоторое давление 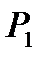 (процесс 2-3). Затем краном соединяют баллон с атмосферой, и газ, адиабатически расширяясь, охлаждается (процесс 3-4), его давление падает до величины (процесс 2-3). Затем краном соединяют баллон с атмосферой, и газ, адиабатически расширяясь, охлаждается (процесс 3-4), его давление падает до величины 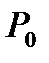 , а температура - до величины , а температура - до величины 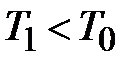 . В момент достижения давления . В момент достижения давления 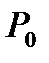 кран К перекрывается и газ изохорически нагревается до комнатной температуры (процесс 4-5). В конечном состоянии давление газа кран К перекрывается и газ изохорически нагревается до комнатной температуры (процесс 4-5). В конечном состоянии давление газа 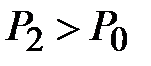 , а температура равна , а температура равна  . .
Масса газа, находящегося в баллоне, в начальном состоянии выражается соотношением Нетрудно видеть, что в течение всех рассмотренных термодинамических процессов масса газа в баллоне больше или равна Назовем массу Введем обозначения
Вывод выражения (2-6.2 ) приводится в Приложении. Измерив значения 1. При адиабатическом расширении (процесс 3-4) кран баллона должен быть перекрыт в момент, когда давление в баллоне станет равным 2. Время выпуска газа должно быть достаточно мало, так, чтобы теплообменом с окружающим воздухом можно было пренебречь. Практически эти условия выполнить трудно, что приводит к ошибкам в определении После открытия крана (процесс 3-4) давление в баллоне со временем уменьшается по экспоненциальному закону и через 0.1 секунды отличается от Однако вручную открыть кран на 0,1 секунды трудно, практически время это оказывается значительно больше. Рассмотрим влияние времени, в течение которого после достижения давления Предположим, что после достижения давления Рассмотрим детальнее процесс нагревания газа на участке (4-6). За счет теплопроводности через стенки баллона за время
где Уравнение баланса энергии для газа, находящегося в баллоне, может быть записано в виде
Разделив переменные и подставив
Последнее выражение можно представить как
его интегрирование дает:
где
откуда
Обозначим температуру газа в баллоне в момент Окончательно соотношение (2-6.5) примет вид
где учтено выражение (1) и то обстоятельство, что точки 3 и 7 лежат на одной изотерме. После того как в момент времени t кран К перекрывается, нагрев газа в баллоне также продолжается, но уже изохорически. Давление газа в конце концов достигает величины
С другой стороны, из уравнения адиабаты (участок 3-4) имеем:
Воспользуемся формулой бинома Ньютона, пренебрегая членами второго порядка малости:
И учитывая, что
Решая совместно уравнения (2-6.6),(2-6.7),( 2-6.8) и снова пренебрегая слагаемыми второго порядка малости, получим
Это уравнение учитывает как теплообмен с окружающей средой, так и уход части газа из баллона в процессе нагрева. Уравнение позволяет найти
График зависимости
Потенцируя выражение (10) и преобразуя его, получим
Порядок выполнения работы Закрыть кран и накачать воздух в баллон (процесс1-2) так, чтобы величина Обработка результатов
 от t и экстраполировать его до пересечения с осью ординат (рис.3). Величина отрезка «b», отсекаемая на отрезке ординат позволяет найти величину от t и экстраполировать его до пересечения с осью ординат (рис.3). Величина отрезка «b», отсекаемая на отрезке ординат позволяет найти величину 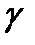 по формуле (2-6.11). по формуле (2-6.11).
В данной работе зависимость Контрольные вопросы и задания 1. Что называется теплоемкостью газа? 2. Какова размерность этой физической величины? 3. Что понимается под удельной и малярной теплоемкостями газа? 4. Как они связаны между собой? Какова связь между 5. Получите уравнение Роберт Майера. Сколько степеней свободы имеют молекулы газов Нe, Н2, СО2? 6. Какие это степени свободы? В каком газе показатель адиабаты 7. Почему в данном эксперименте целесообразно использовать сосуд возможно большего диаметра? 8. Получите уравнение адиабаты в перемененных PT и TV. Какие явления нарушают адиабатичность расширения газа? 9. Как повлияет на ход эксперимента наличие паров воды в воздухе? Список рекомендуемой литературы 1. Матвеев А.Н. Молекулярная физика. М. : Высш. шк., 1988. 2. Булкин П.С., Попова И.И. Общий физический практикум. М. : МГУ, 1988. 3. Основы физики. Курс общей физики. Т.2. Квантовая и статистическая физика / Под. ред. Ю.М. Ципенюка. М. : Физ.-мат. лит., 2001. Лабораторная работа № 2-7 Теплоемкость твердых тел |
|
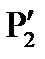 P0
P0
 .
. .
. и
и  . Тогда величина
. Тогда величина  .
.
 и
и  , можно было бы рассчитать величину
, можно было бы рассчитать величину  ;
; , за это время за счет теплообмена со стенками баллона и расширения газа происходит изобарический нагрев газа (процесс 4-6). После того как кран закрывается (точка 6), происходит изохорический нагрев газа (процесс 6-7), давление в баллоне достигает величины
, за это время за счет теплообмена со стенками баллона и расширения газа происходит изобарический нагрев газа (процесс 4-6). После того как кран закрывается (точка 6), происходит изохорический нагрев газа (процесс 6-7), давление в баллоне достигает величины 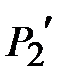 (точка 7). Точка 7 лежит на той же изотерме, что точки 3 и 5, но
(точка 7). Точка 7 лежит на той же изотерме, что точки 3 и 5, но  Очевидно, что
Очевидно, что  зависит от времени выхода газа из баллона, и значение
зависит от времени выхода газа из баллона, и значение  газ будет получать количество теплоты
газ будет получать количество теплоты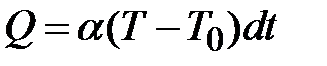 ,
, . Здесь
. Здесь  - температура газа в баллоне,
- температура газа в баллоне, 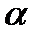 - коэффициент теплопроводности стекла,
- коэффициент теплопроводности стекла,  и
и  - толщина и площадь стенок баллона соответственно.
- толщина и площадь стенок баллона соответственно.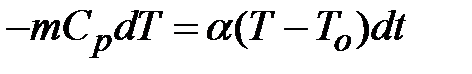 .
.
 из уравнения Менделеева-Клапейрона, получим
из уравнения Менделеева-Клапейрона, получим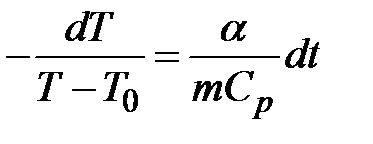 или
или  .
. , (2-6.4)
, (2-6.4) ,
,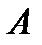 постоянная интегрирования.
постоянная интегрирования.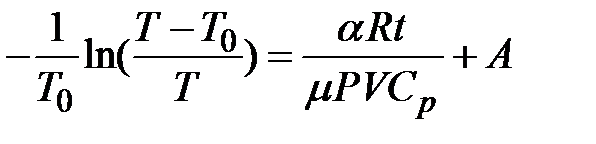 ,
, .
.
 (точка 4) через
(точка 4) через 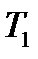 , а
, а 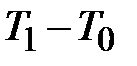 через
через 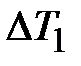 , тогда постоянная интегрирования А будет равна
, тогда постоянная интегрирования А будет равна 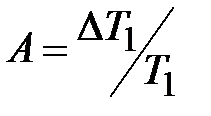 .
.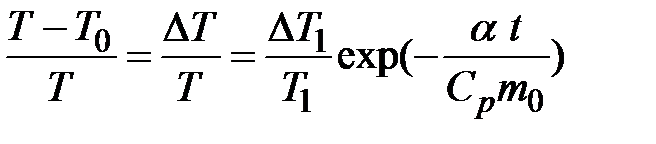 ,
,
 . Для изохорического процесса
. Для изохорического процесса 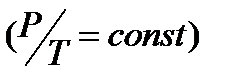 (участок 6-7) имеем
(участок 6-7) имеем или
или  .
.
 .
. .
.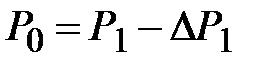 , получим
, получим и
и  .
.
 .
.
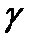 по измеренным при разных величинах
по измеренным при разных величинах  значениями
значениями  и
и 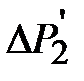 . Прологарифмируем выражение (2-6.9):
. Прологарифмируем выражение (2-6.9): .
. от t является линейной функцией. Если экстраполировать этот график по t = 0, то он будет отсекать на оси ординат отрезок
от t является линейной функцией. Если экстраполировать этот график по t = 0, то он будет отсекать на оси ординат отрезок .
.
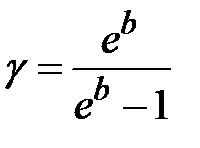 .
.
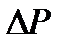 , показываемая манометром, составляла 20-25 см водного столба. Выждать не менее 2 минут, пока температуры воздуха в баллоне и окружающем пространстве не станут одинаковыми (процесс 2-3). Измерить установившееся значение величины
, показываемая манометром, составляла 20-25 см водного столба. Выждать не менее 2 минут, пока температуры воздуха в баллоне и окружающем пространстве не станут одинаковыми (процесс 2-3). Измерить установившееся значение величины  . Повернув кран, соединить баллон с атмосферой и одновременно включить секундомер. Спустя t = 55 секунд снова закрыть кран баллона (точка 6). Через некоторое время (не менее 2 минут), необходимое для выравнивания температуры газа в баллоне и окружающей среде (процесс 6-7), снова записать показание манометра
. Повернув кран, соединить баллон с атмосферой и одновременно включить секундомер. Спустя t = 55 секунд снова закрыть кран баллона (точка 6). Через некоторое время (не менее 2 минут), необходимое для выравнивания температуры газа в баллоне и окружающей среде (процесс 6-7), снова записать показание манометра  . Аналогично провести измерения для времени выдержки t=50, 40, 30, 20,15, 10 и 5 секунд. Для каждого времени выдержки опыт повторить 2 раза.
. Аналогично провести измерения для времени выдержки t=50, 40, 30, 20,15, 10 и 5 секунд. Для каждого времени выдержки опыт повторить 2 раза.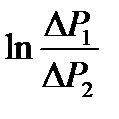
 от t и оценка величины
от t и оценка величины  и
и  и числом степеней свободы молекул газа?
и числом степеней свободы молекул газа?