ОСНОВНЫЕ ЗАДАЧИ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ И ЕЕ ПРИМЕНЕНИЕ В ПСИХОЛОГО-ПЕДАГОГИЧЕСКИХ НАУКАХ. ШКАЛИРОВАНИЕ, ВИДЫ ШКАЛ ИХ РАЗЛИЧИЕ И СПОСОБЫ ИХ ОРГАНИЗАЦИИ.

ЛЕЙБОВСКИЙ М.А.

«МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»

Курс лекций для студентов
Психолого-педагогических специальностей

Данный курс лекций основан на материале прочитанных автором лекций в различных вузах Москвы и на материале учебной литературы, список которой приведен в конце.

ОГЛАВЛЕНИЕ

1. ОСНОВНЫЕ ЗАДАЧИ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ И ЕЕ ПРИМЕНЕНИЕ В ПСИХОЛОГО-ПЕДАГОГИЧЕСКИХ НАУКАХ. ШКАЛИРОВАНИЕ, ВИДЫ ШКАЛ ИХ РАЗЛИЧИЕ И СПОСОБЫ ИХ ОРГАНИЗАЦИИ.......................................... 4

Измерительные шкалы..................................................................................................................... 11

2. ПРОГРАММНЫЕ ПРОДУКТЫ (ППП) ДЛЯ ОБРАБОТКИ ПСИХОЛОГО-ПЕДАГОГИЧЕСКОЙ И СОЦИОЛОГИЧЕСКОЙ ИНФОРМАЦИИ................. 21

3. СТАТИСТИЧЕСКИЙ АНАЛИЗ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ. МЕТОДЫ ПЕРВИЧНОЙ ОБРАБОТКИ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА................... 25

4. ОСНОВНЫЕ ПОНЯТИЯ, ИСПОЛЬЗУЕМЫЕ В МАТЕМАТИЧЕСКОЙ ОБРАБОТКЕ ПСИХОЛОГИЧЕСКИХ ДАННЫХ..................................................................... 34

5. СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ................................................................ 39

6. ВЫЯВЛЕНИЕ РАЗЛИЧИЙ В УРОВНЕ ИССЛЕДУЕМОГО ПРИЗНАКА... 53

7. ОЦЕНКА ДОСТОВЕРНОСТИ СДВИГА В ЗНАЧЕНИЯХ ИССЛЕДУЕМОГО ПРИЗНАКА.......................................................................................................... 79

8. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ................................................................... 106

9. ФАКТОРНЫЙ И КЛАСТЕРНЫЙ АНАЛИЗ. ФАКТОРНЫЙ АНАЛИЗ..... 120

Литература....................................................................................................... 133

ОБРАЗОВАТЕЛЬНЫЕ ИНТЕРНЕТ РЕСУРСЫ............................................... 133

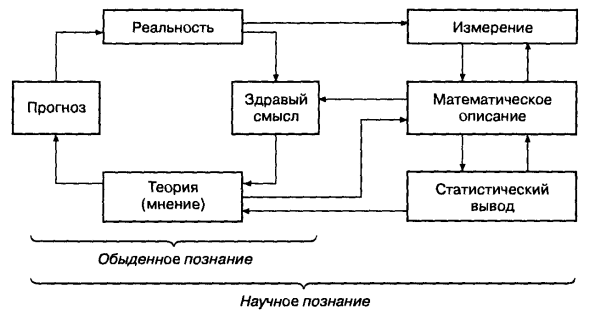
ОСНОВНЫЕ ЗАДАЧИ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ И ЕЕ ПРИМЕНЕНИЕ В ПСИХОЛОГО-ПЕДАГОГИЧЕСКИХ НАУКАХ. ШКАЛИРОВАНИЕ, ВИДЫ ШКАЛ ИХ РАЗЛИЧИЕ И СПОСОБЫ ИХ ОРГАНИЗАЦИИ.

Исследование в любой области, в том числе и в психологии, предполагает получение результатов — обычно в виде чисел. Однако просто собрать данные недостаточно. Даже объективно и корректно собранные данные ничего не говорят. Исследователю необходимо умение организовать их, обработать и проинтерпретировать, что невозможно без знания основ статистики, применения математических методов. Конечно, можно сослаться на наличие современных компьютерных программ, применение которых сейчас становится нормой для исследователя. Но любая программа обработки данных переводит один набор чисел в другой набор чисел. При этом предлагается богатый набор способов такого преобразования, замечательным образом расширяющий возможности анализа данных. И для использования этих возможностей психолог должен уметь:

а) организовать исследование так, чтобы его результаты были доступны обработке в соответствии с проблемами исследования;

б) правильно выбрать метод обработки;

в) содержательно интерпретировать результаты обработки.

Эти умения не заменят ни компьютерная программа, ни математик и программист, придумавшие и написавшие данную программу. Таким образом, применение математики как общенаучного метода, наряду с экспериментом, неизбежно приобретает в психологии свои особенности, связанные со спецификой предмета.

При этом соотношение обыденного и научного познания приведено на рис. 1.

Рис. 1. Соотношение обыденного и научного познания.

Иными словами – необходимо научиться отвечать на самый простой и вечный вопрос: «Да» или «Нет». Только что «Да» и что «Нет». Например, есть ли разница в уровне тревожности до и после тренинга, есть ли зависимость между теми или иными признаками и т.д. И самое главное – насколько можно верить сделанным утверждениям и какова цена ошибки. Именно поэтому неотъемлемой частью подготовки полноценного специалиста-психолога является изучение не только экспериментальной психологии, но и математических методов психологического исследования.

Существует мнение, неоднократно высказывавшееся крупными учеными прошлого: область знания становится наукой, лишь применяя математику. С этим мнением, возможно, не согласятся многие гуманитарии. А зря: именно математика позволяет количественно сравнивать явления, проверять правильность словесных утверждений и тем самым добираться до истины либо приближаться к ней. Математика делает обозримыми длинные и подчас туманные словесные описания, проясняет и экономит мысль.

Математические методы позволяют обоснованно прогнозировать будущие события, вместо того, чтобы гадать на кофейной гуще или как-либо иначе. В общем, польза от применения математики велика, но и труда на ее освоение требуется много. Однако он окупается сполна.

Психология в своем научном становлении неизбежно должна была пройти и прошла путь математизации, хотя не во всех странах и не в полной мере. Точной даты начала пути математизации, пожалуй, не знает ни одна наука. Однако для психологии в качестве условной даты начала этого пути можно принять 18 апреля 1822 г. Именно тогда в Королевском немецком научном обществе Иоганн Фридрих Гербарт прочел доклад «О возможности и необходимости применять в психологии математику». Основная идея доклада сводилась к упомянутому выше мнению: если психология хочет быть наукой, подобно физике, в ней нужно и можно применять математику.

Спустя два года после этого программного по своей сути доклада И. Ф. Гербарт издал книгу «Психология как наука, заново основанная на опыте, метафизике и математике». Эта книга примечательна во многих отношениях. Она явилась первой попыткой создания психологической теории, опирающейся на тот круг явлений, которые непосредственно доступны каждому субъекту, а именно на поток представлений, сменяющих друг друга в сознании. Никаких эмпирических данных о характеристиках этого потока, полученных, подобно физике, экспериментальным путем, тогда не существовало. Поэтому Гербарт в отсутствие этих данных, как он сам писал, должен был придумывать гипотетические модели борьбы всплывающих и исчезающих в сознании представлений. Облекая эти модели в аналитическую форму, например φ =α(l-exp[-βt]) ,где t—время, φ—скорость изменения представлений, α и β — константы, зависящие от опыта, Гербарт, манипулируя числовыми значениями параметров, пытался описать возможные характеристики смены представлений.

По-видимому, И. Ф. Гербарту первому принадлежит мысль о том, что свойства потока сознания — это величины и, следовательно, они в дальнейшем развитии научной психологии подлежат измерению. Ему также принадлежит идея «порога сознания», и он первый употребил выражение «математическая психология».

У И. Ф. Гербарта в Лейпцигском университете нашелся ученик и последователь, позднее ставший профессором философии и математики, — Мориц-Вильгельм Дробиш. Он воспринял, развил и по-своему реализовал программную идею учителя. В словаре Брокгауза и Ефрона о Дробише сказано, что еще в 30-х годах Х1Х века он занимался исследованиями по математике и психологии и публиковался на латинском языке. Но в 1842 г. М.В.Дробиш издал в Лейпциге на немецком языке монографию под недвусмысленным названием: «Эмпирическая психология согласно естественнонаучному методу».

Книга М.-В. Дробиша дает замечательный пример первичной формализации знаний в области психологии сознания. Там нет математики в смысле формул, символики и расчетов, но там есть четкая система понятий о характеристиках потока представлений в сознании как взаимосвязанных величинах. Уже в предисловии М.-В. Дробиш написал, что эта книга предваряет другую, уже готовую, — имеется в виду книга по математической психологии. Но поскольку его коллеги-психологи недостаточно подготовлены в математике, постольку он счел необходимым продемонстрировать эмпирическую психологию сначала безо всякой математики, а лишь на твердых естественнонаучных основах.

Лишь через восемь лет, в 1850 г. в Лейпциге вышла в свет вторая основополагающая книга М.-В. Дробиша—«Первоосновы математической психологии». Таким образом, у этой психологической дисциплины тоже есть точная дата появления в науке. Некоторые современные психологи, пишущие в области математической психологии, ухитряются начинать ее развитие с американского журнала, появившегося в 1963 г. Воистину, «все новое — это хорошо забытое старое». Целое столетие до американцев развивалась математическая психология, точнее — математизированная психология. И начало процессу математизации нашей науки положили И. Ф. Гербарт и М.-В. Дробиш.

Надо сказать, что по части новаций математическая психология Дробиша уступает сделанному его учителем — Гербартом. Правда, Дробиш к двум борющимся в сознании представлениям добавил третье, а это сильно усложнило решения. Но главное, по-моему, в другом. Большую часть объема книги составляют примеры численного моделирования. К сожалению, ни современники, ни потомки не поняли и не оценили научного подвига, совершенного М.-В. Дробишем: у него ведь не было компьютера для численного моделирования. А в современной психологии математическое моделирование — это продукт второй половины XX века. В предисловии к нечаевскому переводу гербартианской психологии российский профессор А. И. Введенский, знаменитый своей «психологией без всякой метафизики», весьма пренебрежительно отозвался о попытке Гербарта применять в психологии математику. Но не такова была реакция естествоиспытателей. И психофизики, в частности Теодор Фехнер, и знаменитый Вильгельм Вундт, работавшие в Лейпциге, не могли пройти мимо основополагающих публикаций И.Ф.Гербартаи М.-В. Дробиша. Ведь именно они математически реализовали в психологии идеи Гербарта о психологических величинах, порогах сознания, времени реакций сознания человека, причем реализовали с использованием современной им математики.

Основные методы тогдашней математики—дифференциальное и интегральное исчисления, уравнения сравнительно несложных зависимостей — оказались вполне пригодными для выявления и описания простейших психофизических законов и различных реакций человека. Но они не годились для изучения сложных психических явлений и сущностей. Не зря В.Вундт категорически отрицал возможность эмпирической психологии исследовать высшие психические функции. Они оставались, по Вундту, в ведении особой, по сути метафизической, психологии народов.

Математические средства для изучения сложных многомерных объектов, в том числе высших психических функции — интеллекта, способностей, личности, стали создавать англоязычные ученые. Среди других результатов оказалось, что рост потомков как бы стремится возвратиться к среднему росту предков. Появилось понятие «регрессия», и были получены уравнения, выражающие эту зависимость. Был усовершенствован коэффициент, раньше предложенный французом Бравэ. Этот коэффициент количественно выражает соотношение двух изменяющихся переменных, т. е. корреляцию. Теперь этот коэффициент — одно из важнейших средств многомерного анализа данных, даже символ сохранил аббревиатурный: малое латинское «r» от английского relation — отношение.

Еще будучи студентом Кембриджа, Фрэнсис Гальтон заметил, что рейтинг успешности сдачи экзаменов по математике, а это был выпускной экзамен, —- изменяется от нескольких тысяч до немногих сотен баллов. Позднее, связав это с распределением талантов, Гальтон пришел к мысли о том, что специальные испытания позволяют прогнозировать дальнейшие жизненные успехи людей. Так в 80-х гг. XIX века родился гальтоновский метод тестов.

Идею тестов подхватили и развили французы А. Бит, В. Анри и другие, создавшие первые тесты для селекции социально отсталых детей. Это послужило началом психологической тестологии, что, в свою очередь, повлекло за собой развитие психологических измерений.

Большие массивы числовых результатов измерений по тестам— в баллах, стали объектом многочисленных исследований, в том числе математико-психологических. Особая роль здесь принадлежит английскому инженеру, работавшему в Америке, —Чарльзу Спирмену.

Во-первых, Ч. Спирмен, полагавший, что для вычисления корреляции между рядами целочисленных баллов, или рангов, нужна специальная мера, перепробовав разные варианты (1904 г.), остановился, наконец, на той форме коэффициента корреляции рангов, которая с тех пор носит его имя.

Во-вторых, имея дело с большими массивами числовых результатов по тестам и корреляций между этими результатами, Ч. Спирмен предположил, что эти корреляции вовсе не выражают взаимовлияние результатов, а эксплицируют их совместную изменчивость под влиянием обшей латентной психической причины, или фактора, например интеллекта. Соответственно этому Спирмен предложил теорию «генерального» фактора, определяющего совместную изменчивость переменных тестовых результатов, а также разработал метод выявления этого фактора по корреляционной матрице. Это был первый метод факторного анализа, созданный в психологии и для психологических целей.

У однофакторной теории Ч. Спирмена быстро нашлись оппоненты. Противоположную, многофакторную теорию, объясняющую корреляции, предложил Леон Терстоун. Ему же принадлежит первый метод мультифакторного анализа, основанный на применении линейной алгебры. После Ч. Спирмена и Л. Терстоуна факторный анализ, не только стал одним из важнейших математических методов многомерного анализа данных в психологии, но и вышел далеко за ее пределы, превратился в общенаучный метод анализа, данных.

С конца 20-х г.г. XX века математические методы все шире проникают в психологию и творчески используются в ней. Интенсивно развивается психологическая теория измерений. На основе аппарата цепей Маркова разрабатываются стохастические модели научения в психологии поведения. Созданный в области биологии Рональдом Фишером дисперсионный анализ становится основным математическим методом в генетической психологии. Математические модели из теории автоматического регулирования и шенноновская теория информации широко применяются в инженерной и общей психологии. В итоге современная научная психология во многих своих отраслях математизирована значительным образом (следует отметить, что многие современные ученые-психологи в качестве первого базового образования имеют математическое или техническое). При этом вновь появляющиеся математические новации нередко заимствуются психологами для своих целей. К примеру, появление алгоритмического языка для задач управления, предложенного А. А. Ляпуновым и Г. А. Шестопалом, почти сразу же было использовано В.Н.Пушкиным для составления алгоритмов деятельности железнодорожного диспетчера.

Любой вид измерения предполагает наличие единиц измерения Единица измерения это та «измерительная палочка», как говорил С. Стивнес, которая является условным эталоном для осуществления тех или иных измерительных процедур. В естественных науках и технике существуют стандартные единицы измерения, например, градус, метр, ампер и т.д.

Психологические переменные за единичными исключениями не имеют собственных измерительных единиц. Поэтому в большинстве случаев значение психологического признака определяется при помощи специальных измерительных шкал.

Измерительные шкалы

Существует 4 основных типа измерительных шкал.

Номинативная шкала- это шкала, классифицирующая по названию: потеп (лат.) - имя, название. Название же не измеряется количественно, оно лишь позволяет отличить один объект от другого или одного субъекта от другого. Номинативная шкала - это способ классификации объектов или субъектов, распределения их по ячейкам классификации.

Простейший случай номинативной шкалы - дихотомическая шкала, состоящая всего лишь из двух ячеек, например: "имеет братьев и сестер - единственный ребенок в семье"; "иностранец - соотечественник"; "проголосовал "за" - проголосовал "против"" и т.п.

Признак, который измеряется по дихотомической шкале наименований, называется альтернативным. Он может принимать всего два значения. При этом исследователь зачастую заинтересован в одном из них, и тогда он говорит, что признак "проявился", если тот принял интересующее его значение, и что признак "не проявился", если он принял противоположное значение. Например: "Признак леворукости проявился у 8 испытуемых из 20". В принципе номинативная шкала может состоять из ячеек "признак проявился - признак не проявился".

Более сложный вариант номинативной шкалы - классификация из трех и более ячеек, например: "экстрапунитивные - интрапунитивные - импунитивные реакции" или "выбор кандидатуры А - кандидатуры Б - кандидатуры В - кандидатуры Г" или "старший - средний - младший -единственный ребенок всемье" и др.

Расклассифицировав все объекты, реакции или всех испытуемых по ячейкам классификации, мы получаем возможность от наименований перейти к числам, подсчитав количество наблюдений в каждой из ячеек.

Как уже указывалось, наблюдение - это одна зарегистрированная реакция, один совершенный выбор, одно осуществленное действие или результат одного испытуемого.

Допустим, мы определим, что кандидатуру А выбрали 7 испытуемых, кандидатуру Б - 11, кандидатуру В - 28, акандидатуру Г - всего 1. Теперь мы можем оперировать этими числами, представляющими собой частоты встречаемости разных наименований, то есть частоты принятия признаком "выбор" каждого из 4 возможных значении. Далее мы можем сопоставить полученное распределение частот с равномерным или каким-то иным распределением.

Таким образом, номинативная шкала позволяет нам подсчитывать частоты встречаемости разных "наименований", или значений признака, и затем работать с этими частотами с помощью математических методов.

Единица измерения, которой мы при этом оперируем - количество наблюдений (испытуемых, реакций, выборов и т. п.), или частота. Точнее, единица измерения - это одно наблюдение. Такие данные могут быть обработаны с помощью метода χ²,биномиального критерия m и углового преобразования Фишера φ*.

Порядковая шкала (ранговая)- это шкала, классифицирующая по принципу "больше - меньше". Если в шкале наименований было безразлично, в каком порядке мы расположим классификационные ячейки, то в порядковой шкале они образуют последовательность от ячейки "самое малое значение" к ячейке "самое большое значение" (или наоборот). Ячейки теперь уместнее называть классами, поскольку по отношению к классам употребимы определения "низкий", "средний" и "высокий" класс, или 1-й, 2-й, 3-й класс, и т.д.

В порядковой шкале должно быть не менее трех классов, например "положительная реакция - нейтральная реакция - отрицательная реакция" или "подходит для занятия вакантной должности - подходит с оговорками - не подходит" и т. п.

В порядковой шкале мы не знаем истинного расстояния между классами, а знаем лишь, что они образуют последовательность. Например, классы "подходит для занятия вакантной должности" и "подходит с оговорками" могут быть реально ближе друг к другу, чем класс подходит с оговорками" к классу "не подходит".

От классов легко перейти к числам, если мы условимся считать, что низший класс получает ранг 1, средний класс - ранг 2, а высший класс - ранг 3, или наоборот. Чем больше классов в шкале, тем больше. У нас возможностей для математической обработки полученных данных и проверки статистических гипотез.

Например, мы можем оценить различия между двумя выборками испытуемых по преобладанию у них более высоких или более низких рангов или подсчитать коэффициент ранговой корреляции между двумя переменными, измеренными в порядковой шкале, допустим, между оценками профессиональной компетентности руководителя, данными ему разными экспертами.

Все психологические методы, использующие ранжирование, построены на применении шкалы порядка. Если испытуемому предлагается упорядочить 18 ценностей по степени их значимости для него, проранжировать список личностных качеств социального работника или 10 претендентов на эту должность по степени их профессиональной пригодности, то во всех этих случаях испытуемый совершает так называемое принудительное ранжирование, при котором количество рангов соответствует количеству ранжируемых субъектов или объектов (ценностей, качеств и т.п.).

Независимо от того, приписываем ли мы каждому качеству или испытуемому один из 3-4 рангов или совершаем процедуру принудительного ранжирования, мы получаем в обоих случаях ряды значении, измеренные по порядковой шкале. Правда, если у нас всего 3 возможных класса и, следовательно, 3 ранга, и при этом, скажем, 20 ранжируемых испытуемых, то некоторые из них неизбежно получат одинаковые ранги. Все многообразие жизни не может уместиться в 3 градации, поэтому в один и тот же класс могут попасть люди, достаточно серьезно различающиеся между собой. С другой стороны, принудительное ранжирование, то есть образование последовательности из многих испытуемых, может искусственно преувеличивать различия между людьми. Кроме того, данные, полученные в разных группах, могут оказаться несопоставимыми, так как группы могут изначально различаться по уровню развития исследуемого качества, и испытуемый, получивший водной группе высший ранг, в другой получил бы всего лишь средний, и т.п.

Выход из положения может быть найден, если задавать достаточно дробную классификационную систему, скажем, из 10 классов, или градаций, признака. В сущности, подавляющее большинство психологических методик, использующих экспертную оценку, построено на измерении одним и тем же "аршином" из 10, 20 или даже 100 градаций разных испытуемых в разных выборках.

Итак, единица измерения в шкале порядка - расстояние в 1 класс или в 1 ранг, при этом расстояние между классами и рангами может быть разным (оно нам неизвестно). К данным, полученным по порядковой шкале, применимы все описанные в данной книге критерии и методы.

Интервальная шкала- это шкала, классифицирующая по принципу "больше на определенное количество единиц - меньше на определенное количество единиц". Каждое из возможных значений признака отстоит от другого на равном расстоянии.

Можно предположить, что если мы измеряем время решения задачи в секундах, то это уже явно шкала интервалов. Однако на самом деле это не так, поскольку психологически различие в 20 секунд между испытуемым А и Б может быть отнюдь не равно различию в 20 секунд между испытуемыми Б и Г, если испытуемый А решил задачу за 2 секунды, Б - за 22, В - за 222, а Г - за 242.

Аналогичным образом, каждая секунда после истечения полутора минут в опыте с измерением мышечного волевого усилия на динамометре с подвижной стрелкой, по "цене", может быть, равна 10 или даже более секундам в первые полминуты опыта. "Одна секунда за год идет" - так сформулировал это однажды один испытуемый.

Попытки измерять психологические явления в физических единицах - волю в секундах, способности в сантиметрах, а ощущение собственной недостаточности - в миллиметрах и т. п., конечно, понятны, ведь все-таки это измерения в единицах "объективно" существующего времени и пространства. Однако ни один опытный исследователь при этом не обольщает себя мыслью, что он совершает измерения по психологической интервальной шкале. Эти измерения принадлежат по-прежнему к шкале порядка, нравится нам это или нет.

Можно с определенной долей уверенности утверждать лишь, что испытуемый А решил задачу быстрее Б, Б быстрее В, а В быстрее Г.

Аналогичным образом, значения, полученные испытуемыми в баллах по любой нестандартизованной методике, оказываются измеренными лишь по шкале порядка. На самом деле равно интервальными можно считать лишь шкалы в единицах стандартного отклонения и процентильные шкалы, и то лишь при условии, что распределение значений в стандартизующей выборке было нормальным.

Принцип построения большинства интервальных шкал построен на известном правиле "трех сигм": примерно 97,7-97,8% всех значений признака при нормальном его распределении укладываются в диапазоне М±3δ. Можно построить шкалу в единицах долей стандартного отклонения, которая будет охватывать весь возможный диапазон изменения признака, если крайний слева и крайний справа интервалы оставить открытыми (подробнее об этом будет сказано позже).

Р.Б. Кеттелл предложил, например, шкалу стенов - "стандартной десятки". Среднее арифметическое значение в "сырых" баллах принимается за точку отсчета. Вправо и влево отмеряются интервалы, равные 1/2 стандартного отклонения. На Рис. 2представлена схема вычисления стандартных оценок и перевода "сырых" баллов в стены по шкале N 16-факторного личностного опросника Р. Б. Кеттелла.

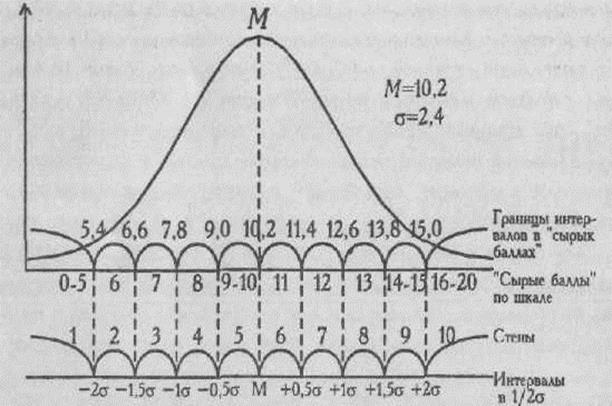
Рис. 2. Схема вычисления стандартных оценок (стенов) по фактору N 16- факторного личностного опросника Р. Б. Кеттелла; снизу указаны интервалы в единицах 1/2 стандартного отклонения

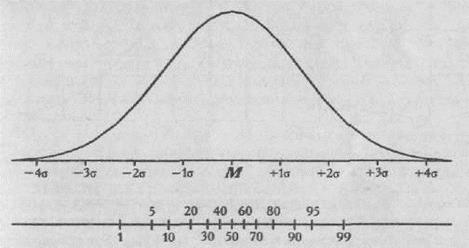
Справа от среднего значения будут располагаться интервалы, равные 6, 7, 8, 9 и 10 стенам, причем последний из этих интервалов открыт. Слева от среднего значения будут располагаться интервалы, равные 5, 4, 3, 2 и 1 стенам, и крайний интервал также открыт. Теперь мы поднимаемся вверх, к оси "сырых баллов", и размечаем границы интервалов в единицах "сырых" баллов. Поскольку М=10,2; δ=2,4, вправо мы откладываем 1/2δ т.е. 1,2 "сырых" балла. Таким образом, граница интервала составит: (10,2 + 1,2) = 11,4 "сырых" балла. Итак, границы интервала, соответствующего 6 стенам, будут простираться от 10,2 до 11,4 баллов. В сущности, в него попадает только одно "сырое" значение - 11 баллов. Влево от средней мы откладываем 1/2δ и получаем границу интервала: 10,2-1,2=9. Таким образом, границы интервала, соответствующие 9 стенам, простираются от 9 до 10,2. В этот интервал попадают уже два "сырых" значения - 9 и 10. Если испытуемый получил 9 "сырых" баллов, ему начисляется теперь 5 стенов; если он получил 11 "сырых" баллов - 6 стенов, и т. д.

Мы видим, что в шкале стенов иногда за разное количество "сырых" баллов будет начисляться одинаковое количество стенов. Например, за 16, 17, 18, 19 и 20 баллов будет начисляться 10 стенов, а за 14 и 15 - 9 стенов и т. д.

В принципе, шкалу стенов можно построить по любым данным, измеренным по крайней мере в порядковой шкале, при объеме выборки п>200 и нормальном распределении признака².

Другой способ построения равно интервальной шкалы - группировка интервалов по принципу равенства накопленных частот. При нормальном распределении признака в окрестности среднего значения группируется большая часть всех наблюдений, поэтому в этой области среднего значения интервалы оказываются меньше, уже, а по мере удаления от центра распределения они увеличиваются, (см. Рис. 3). Следовательно, такая процентильная шкала является равно интервальной только относительно накопленной частоты.

Рис. 3. Процентильная шкала; сверху для сравнения указаны интервалы в единицах стандартного отклонения

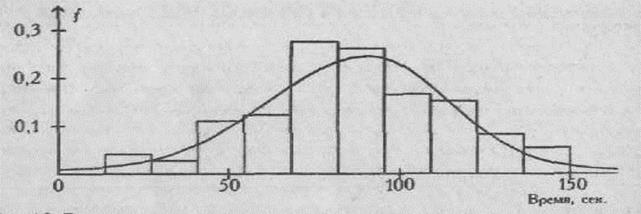
Построение шкал равных интервалов по данным, полученным по шкале порядка, напоминает трюк с веревочной лестницей, на который ссылался С. Стивенс. Мы сначала поднимаемся по лестнице, которая ни на чем не закреплена, и добираемся до лестницы, которая закреплена. Однако каким путем мы оказались на ней? Измерили некую психологическую переменную по шкале порядка, подсчитали средние и стандартные отклонения, а затем получили, наконец, интервальную шкалу. Как отмечал Стивенс "Такому нелегальному использованию статистики может быть дано известное прагматическое оправдание; во многих случаях оно приводит к плодотворным результатам".

Многие исследователи не проверяют степень совпадения полученного ими эмпирического распределения с нормальным распределением, и тем более не переводят получаемые значения в единицы долей стандартного отклонения или процентили, предпочитая пользоваться "сырыми" данными. "Сырые" же данные часто дают скошенное, срезанное по краям или двухвершинное распределение. На Рис. 4 представлено распределение показателя мышечного волевого усилия на выборке из 102 испытуемых. Распределение с удовлетворительной точностью можно считать нормальным (χ²=12,7 при v=9, М=89,75, δ= 25,1).

Рис. 4 Гистограмма и плавная кривая распределения показателя мышечного волевого усилия (n=102)

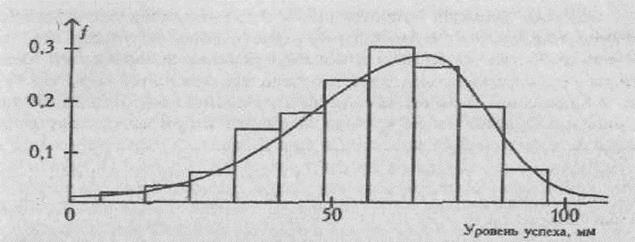
На Рис. 5 представлено распределение показателя самооценки по шкале методики Дж. Менестера - Р.Корзини "Уровень успеха, которого я должен был достичь уже сейчас" (n=356). Распределение значимо отличается от нормального

(χ²⁼58,8, при v=7; p<0,01; М=80,64; δ=16,86).

Рис. 5.Гистограмма и плавная кривая распределения показателя должного успеха (n=356).

С такими "ненормальными" распределениями приходится встречаться очень часто, чаще, может быть, чем с классическими нормальными. И дело здесь не в каком-то изъяне, а в самой специфике психологических признаков. По некоторым методикам от 10 до 20% испытуемых получают оценку "ноль" - например, в их рассказах не встречается ни одной словесной формулировки, которая отражала бы мотив "надежда на успех" или "боязнь неудачи" (методика Хекхаузена). То, что испытуемый получил оценку "ноль", нормально, но распределение таких оценок не может быть нормальным, как бы мы ни увеличивали объем выборки

Шкала отношений

Шкалу отношений называют также шкалой равных отношений. Особенностью этой шкалы является наличие твердо фиксированного нуля, который означает полное отсутствие какого-либо свойства или признака Шкала отношений является наиболее информативной шкалой, допускающей любые математические операции и использование разнообразных статистических методов.

Шкала отношений по сути очень близка интервальной, поскольку если строго фиксировать начало отсчета, то любая интервальная шкала превращается в шкалу отношений

Именно в шкале отношений производятся точные и сверхточные измерения в таких науках, как физика, химия, микробиология и др. Измерение по шкале отношений производятся и в близких к психологии науках, таких, как психофизика, психофизиология, психогенетика.

Очевидно, что все измерения должны проводиться на определенном материале. И здесь следует остановиться на основных определениях, относящихся к понятию Выборка.

Генеральная совокупность — это все множество объектов, в отношении которого формулируется исследовательская гипотеза.

Выборка — это ограниченная по численности группа объектов (в психологии — испытуемых, респондентов), специально отбираемая из генеральной совокупности для изучения ее свойств. Соответственно, изучение на выборке свойств генеральной совокупности называется выборочным исследованием. Практически все психологические исследования являются выборочными, а их выводы распространяются на генеральные совокупности.

Репрезентативность выборки — иными словами, ее представительность — это способность выборки представлять изучаемые явления достаточно полно—с точки зрения их изменчивости в генеральной совокупности.

Стратифицированная выборка, или отбор по свойствам генеральной совокупности (разделение выборки на «страты». Он предполагает предварительное определение тех качеств, которые могут влиять на изменчивость изучаемого свойства (это может быть пол, уровень дохода или образования и т. д.).

Статистическая достоверность, или статистическая значимость, результатов исследования определяется при помощи методов статистического вывода, которые предъявляют определенные требования к численности, или объему выборки.

2. ПРОГРАММНЫЕ ПРОДУКТЫ (ППП) ДЛЯ ОБРАБОТКИ ПСИХОЛОГО-ПЕДАГОГИЧЕСКОЙ И СОЦИОЛОГИЧЕСКОЙ ИНФОРМАЦИИ.

Одним из основных направлений подготовки специалиста является формирование умений подготовки и обработки информации в соответствии со сформулированной гипотезой исследования.

К основным средствам обработки информации относятся наиболее популярные пакеты прикладных программ (ППП), такие как SPSS 19, Statistica 6.0 и др. Кроме того ряд исследований может быть произведен и с использованием табличного процессора Excel.

К основным достоинствам компьютерной обработки информации можно отнести:

1. Универсальность подготовки данных, т.к. во всех пакетах программ предусмотрена возможность конвертации данных из одного приложения в другое. Для начинающего пользователя простейшим способом является первичная подготовка данных в Excel с последующей конвертацией в необходимый ППП, либо запуск ППП с указанием того, что исходные данные подготовлены в Excel.

2. Возможность копирования результатов обработки непосредственно в Word, что позволяет значительно украсить результаты исследования и повысить убедительность полученных данных.

3. Развитая система информационной поддержки с имеющейся литературой и on-line помощниками дающая возможность рассмотреть пошаговые алгоритмы обработки информации.