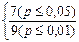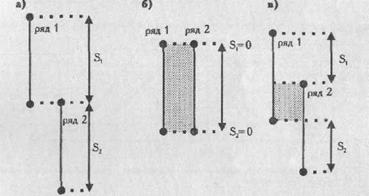
Графическое представление критерия Q

На Рис. 2. представлены три варианта соотношения рядов значений в двух выборках. В варианте (а) все значения первого ряда выше всех значений второго ряда. Различия, безусловно, достоверны, при соблюдении условия, что n_1,n_{2 >} 11.

В варианте (б), напротив, оба ряда находятся на одном и том же уровне: различия недостоверны. В варианте (в) ряды частично перекрещиваются, но все же первый ряд оказывается гораздо выше второго. Достаточно ли велики зоны S₁ и S₂, в сумме составляющие Q, можно определить по Таблице, в которой приведены критические значения Q для разных n. Чем величина Q больше, тем более достоверные различия мы сможем констатировать.

Рис. 2. Возможные соотношения рядов значений в двух выборках:

*S₁ - зона значений 1-го ряда, которые выше максимального значения 2-го ряда;

*S₂ - зона значений второго ряда, которые меньше минимального значения 1-го ряда;

*штриховкой отмечены перекрещивающиеся зоны двух рядов

Ограничения критерия Q

1. Вкаждой из сопоставляемых выборок должно быть не менее 11 наблюдений. При этом объемы выборок должны примерно совпадать. Е.В. Гублером указываются следующие правила:

а) если в обеих выборках меньше 50 наблюдений, то абсолютная величина разности между n₁и n₂не должна быть больше 10 наблюдений;

б) если в каждой из выборок больше 51 наблюдения, но меньше 100, то абсолютная величина разности между n₁ и n₂не должна быть больше 20 наблюдений;

в) если в каждой из выборок больше 100 наблюдений, то допускается, чтобы одна из выборок была больше другой не более чем в 1,5-2 раза.

2. Диапазоны разброса значений в двух выборках должны не совпадать между собой, в противном случае применение критерия бессмысленно. Между тем, возможны случаи, когда

диапазоны разброса значений совпадают, но, вследствие разносторонней асимметрии двух распределений, различия в средних величинах признаков существенны (Рис.3, 4).

Рис. 3. Вариант соотношения распределений признака в двух выборках, при котором критерий Q беспомощен

Рис. 4. Вариант соотношения распределений признака в двух выборках, при котором критерий Q может быть мощным.

Пример

У предполагаемых участников психологического эксперимента, моделирующего деятельность воздушного диспетчера, был измерен уровень вербального и невербального интеллекта с помощью методики Д. Векслера. Было обследовано 26 юношей в возрасте от 18 до 24 лет (средний возраст 20,5 лет). 14 из них были студентами физического факультета, а 12 - студентами психологического факультета Ленинградского университета (Сидоренко Е.В., 1978). Показатели вербального интеллекта представлены в Табл. 2.1.

Можно ли утверждать, что одна из групп превосходит другую по уровню вербального интеллекта?

Таблица 1

Индивидуальные значения вербального интеллекта в выборках студентов физического (n₁=14) и психологического (п₂ =12) факультетов

Упорядочим значения в обеих выборках, а затем сформулируем гипотезы:

H₀: Студенты-физики не превосходят студентов-психологов по уровню вербального интеллекта.

H₁: Студенты-физики превосходят студентов-психологов по уровню вербального интеллекта.

Таблица 2.

Упорядоченные по убыванию вербального интеллекта ряды

индивидуальных значении в двух студенческих выборках

Как видно из Табл. 2, мы правильно обозначили ряды: первый, тот, что "выше" - ряд физиков, а второй, тот, что "ниже" - рядпсихологов.

По Табл. 2 определяем количество значений первого ряда, которые больше максимального значения второго ряда: S₁=5.

Теперь определяем количество значений второго ряда, которые меньше минимального значения первого ряда: S₂=6.

Вычисляем Q_эмппо формуле:

Q_эмп = S₁ + S₂ = 5+6 =11

По Табл.определяем критические значения Q для n₁=14, n₂=12:

Q_кр=

Ясно, что чем больше расхождения между выборками, тем больше величина Q.Н₀ отклоняется при Q_эмп ≥Qкр,а при Q_эмп < Q_кр мы будем вынуждены принять Н_0.

Q_эмп > Q_кр (p≤0.01)

Ответ: H₀ отклоняется.

Принимается H₁. Студенты-физики превосходят студентов-психологов по уровню вербального интеллекта (р<0,01). Отметим, что в тех случаях, когда эмпирическая величина критерия оказывается на границе зоны незначимости, мы имеем право утверждать лишь, что различия достоверны при р<0,05, если же оно оказывается между двумя критическими значениями, то мы можем утверждать, что р< 0,05.

Если эмпирическое значение критерия оказывается на границе, мы можем утверждать, что р< 0,01, если оно попадает в зону значимости, мы можем утверждать, что р< 0,01.

Поскольку уровень значимости выявленных различий достаточно высок (р<0,01), мы могли бы на этом остановиться. Однако если исследователь сам психолог, а не физик, вряд ли он на этом остановится. Он может попробовать сопоставить выборки по уровню невербального интеллекта, поскольку именно невербальный интеллект определяет уровень интеллекта в целом и степень его организованности.

Мы вернемся к этому примеру при рассмотрении критерия Манна-Уитни и попытаемся ответить на вопрос о соотношении уровней невербального интеллекта в двух выборках. Быть может, психологи еще окажутся в более высоком ряду!

АЛГОРИТМ