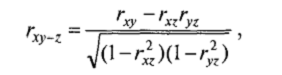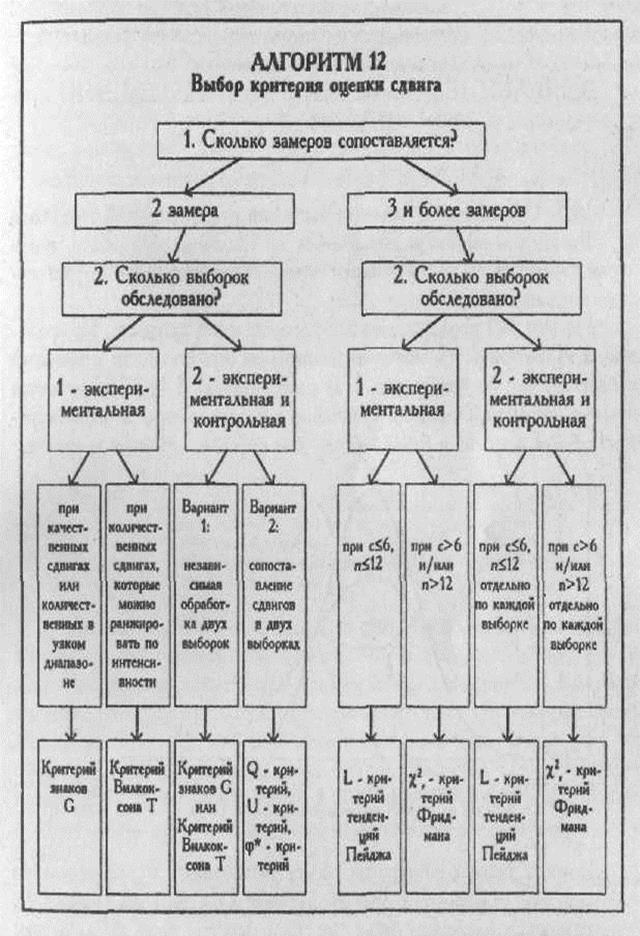
Алгоритм принятия решения о выборе критерия оценки изменений

8. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ

Коэффициент корреляции — двумерная описательная статистика, количественная мера взаимосвязи (совместной изменчивости) двух переменных.

История разработки и применения коэффициентов корреляции для исследования взаимосвязей фактически началась одновременно с возникновением измерительного подхода к исследованию индивидуальных различий — в 1870—1880 гг. Пионером в измерении способностей человека, как и автором самого термина «коэффициент корреляции», был Френсис Гальтон, а самые популярные коэффициенты корреляции были разработаны его последователем Карлом Пирсоном. С тех пор изучение взаимосвязей с использованием коэффициентов корреляции является одним из наиболее популярных в психологии занятием.

К настоящему времени разработано великое множество различных коэффициентов корреляции, проблеме измерения взаимосвязи с их помощью посвящены сотни книг. Поэтому, не претендуя на полноту изложения, мы рассмотрим лишь самые важные, действительно незаменимые в исследованиях меры связи — r_xy--Пирсона, ρ-Спирмена и τ-Кендалла¹. Их общей особенностью является то, что они отражают взаимосвязь двух признаков, измеренных в количественной шкале — ранговой или метрической.

Вообще говоря, любое эмпирическое исследование сосредоточено на изучении взаимосвязей двух или более переменных.

ПРИМЕР

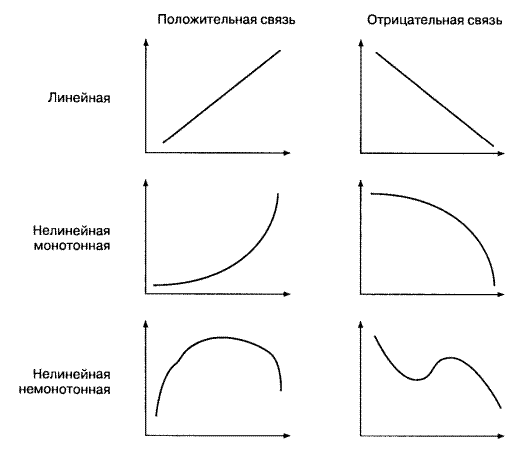
Приведем пример исследования влияния демонстрации сцен насилия по ТВ на агрессивность подростков. 1. Изучается взаимосвязь двух переменных, измеренных в количественной (ранговой или метрической) шкале:

1) «время просмотра телепередач с насилием»;

2) «агрессивность».

Читается как тау-Кендалла.

2. Изучается различие в агрессивности 2-х или более групп подростков, отличающихся длительностью просмотра телепередач с демонстрацией сцен насилия.

Во втором примере изучение различий может быть представлено как исследование взаимосвязи 2-х переменных, одна из которых — номинативная (длительность просмотра телепередач). И для этой ситуации также разработаны свои коэффициенты корреляции.

Любое исследование можно свести к изучению корреляций, благо изобретены самые различные коэффициенты корреляции для практически любой исследовательской ситуации. Но в дальнейшем изложении мы будем различать два класса задач:

□ исследование корреляций — когда две переменные представлены в числовой шкале;

□ исследование различий — когда хотя бы одна из двух переменных представлена в номинативной шкале.

Такое деление соответствует и логике построения популярных компьютерных статистических программ, в которых в меню Корреляции предлагаются три коэффициента (г-Пирсона, r-Спирмена и т-Кендалла), а для решения других исследовательских задач предлагаются методы сравнения групп.

ПОНЯТИЕ КОРРЕЛЯЦИИ

Взаимосвязи на языке математики обычно описываются при помощи функций, которые графически изображаются в виде линий. На рис. 6.1 изображено несколько графиков функций. Если изменение одной переменной на одну единицу всегда приводит к изменению другой переменной на одну и ту же величину, функция является линейной (график ее представляет прямую линию); любая другая связь — нелинейная. Если увеличение одной переменной связано с увеличением другой, то связь — положительная (прямая); если увеличение одной переменной связано с уменьшением другой, то связь — отрицательная (обратная). Если направление изменения одной переменной не меняется с возрастанием (убыванием) другой переменной, то такая функция — монотонная; в противном случае функцию называют немонотонной.

Функциональные связи, подобные изображенным на рис.1, являются идеализациями. Их особенность заключается в том, что одному значению одной переменной соответствует строго определенное значение другой переменной. Например, такова взаимосвязь двух физических переменных — веса и длины тела (линейная положительная). Однако даже в физических экспериментах эмпирическая взаимосвязь будет отличаться от функциональной связи в силу неучтенных или неизвестных причин: колебаний состава материала, погрешностей измерения и пр.

Рис.1 Примеры графиков часто встречающихся функций.

В психологии, как и во многих других науках, при изучении взаимосвязи признаков из поля зрения исследователя неизбежно выпадает множество возможных причин изменчивости этих признаков. Результатом является то, что даже существующая в реальности функциональная связь между переменными выступает эмпирически как вероятностная (стохастическая): одному и тому же значению одной переменной соответствует распределение различных значений другой переменной (и наоборот). Простейшим примером является соотношение роста и веса людей. Эмпирические результаты исследования этих двух признаков покажут, конечно, положительную их взаимосвязь. Но несложно догадаться, что она будет отличаться от строгой, линейной, положительной — идеальной математической функции, даже при всех ухищрениях исследователя по учету стройности или полноты испытуемых. (Вряд ли на этом основании кому-то придет в голову отрицать факт наличия строгой функциональной связи между длиной и весом тела.)

Итак, в психологии, как и во многих других науках, функциональная взаимосвязь явлений эмпирически может быть выявлена только как вероятностная связь соответствующих признаков. Наглядное представление о характере вероятностной связи дает диаграмма рассеивания — график, оси которого соответствуют значениям двух переменных, а каждый испытуемый представляет собой точку (рис. 2). В качестве числовой характеристики вероятностной связи используются коэффициенты корреляции.

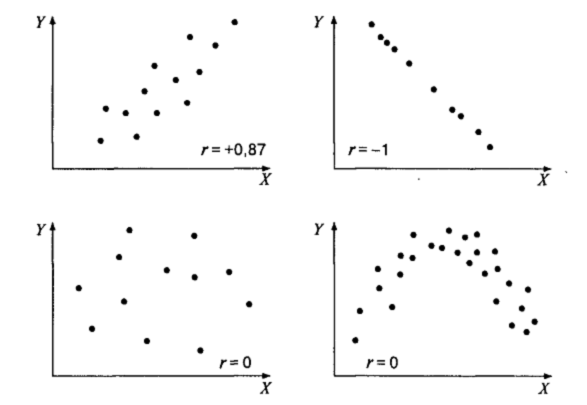
Рис. 2. Примеры диаграмм рассеивания и коэффициентов корреляции.

Коэффициент корреляции — это количественная мера силы и направления вероятностной взаимосвязи двух переменных; принимает значения в диапазоне от —1 до +1.

Сила связи достигает максимума при условии взаимно однозначного соответствия: когда каждому значению одной переменной соответствует только одно значение другой переменной (и наоборот), эмпирическая взаимосвязь при этом совпадает с функциональной линейной связью. Показателем силы связи является абсолютная (без учета знака) величина коэффициента корреляции.

Направление связи определяется прямым или обратным соотношением значений двух переменных: если возрастанию значений одной переменной соответствует возрастание значений другой переменной, то взаимосвязь называется прямой (положительной); если возрастанию значений одной переменной соответствует убывание значений другой переменной, то взаимосвязь является обратной (отрицательной). Показателем направления связи является знак коэффициента корреляции.

Следует отметить еще один важный факт. Когда мы смотрим значение коэффициента корреляции о его значимости можно судить только после того, как мы будем знать объем выборки. Так, одно и то же значение r_xy для одной выборки будет незначимым, а для другой значимым на уровне 0,01. Желающие могут провести следующий эксперимент: для выборки, у которой r_xy оказалось незначимым, надо скопировать ее саму на себя несколько раз. Очевидно, что значение r_xy при этом не изменится, а коэффициент корреляции станет значимым!

КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ r_xy

ПИРСОНА

r-Пирсона (Pearson r) применяется для изучения взаимосвязи двух метрических переменных, измеренных на одной и той же выборке. Существует множество ситуаций, в которых уместно его применение. Влияет ли интеллект на успеваемость на старших курсах университета? Связан ли размер заработной платы работника с его доброжелательностью к коллегам? Влияет ли настроение школьника на успешность решения сложной арифметической задачи? Для ответа на подобные вопросы исследователь должен измерить два интересующих его показателя у каждого члена выборки. Данные для изучения взаимосвязи затем сводятся в таблицу, как в приведенном ниже примере.

ПРИМЕР

В таблице приведен пример исходных данных измерения двух показателей интеллекта (вербального и невербального) у 20 учащихся 8-го класса.

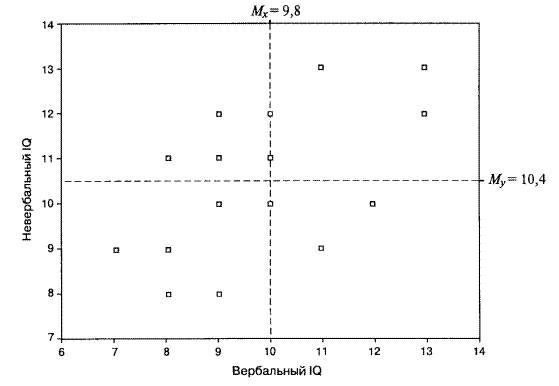
Связь между этими переменными можно изобразить при помощи диаграммы рассеивания (см. рис. 3). Диаграмма показывает, что существует некоторая взаимосвязь измеренных показателей: чем больше значения вербального интеллекта, тем (преимущественно) больше значения невербального интеллекта.

Прежде чем дать формулу коэффициента корреляции, попробуем проследить логику ее возникновения, используя данные примера 6.1. Положение каждой /-точки (испытуемого с номером i) на диаграмме рассеивания относительно остальных точек (рис.3) может быть задано величинами и знаками отклонений соответствующих значений переменных от своих средних величин: (X_j— М_х) и (y_j — M_y). Если знаки этих отклонений совпадают, то это свидетельствует в пользу положительной взаимосвязи (большие значения по у или меньшим значениям по х соответствуют меньшие значения по у).

Рис. 3 Диаграмма рассеивания для примера.

ПРИМЕР

Для испытуемого № 1 отклонение от среднего по х и по у положительное, а для испытуемого № 3 и то и другое отклонения отрицательные. Следовательно, данные того и другого свидетельствуют о положительной взаимосвязи изучаемых признаков. Напротив, если знаки отклонений от средних по х и по у различаются, то это будет свидетельствовать об отрицательной взаимосвязи между признаками. Так, для испытуемого № 4 отклонение от среднего по х является отрицательным, по у — положительным, а для испытуемого № 9 — наоборот.

Таким образом, если произведение отклонений (х_i— Мх)*(y_i — My) положительное, то данные /-испытуемого свидетельствуют о прямой (положительной) взаимосвязи, а если отрицательное — то об обратной (отрицательной) взаимосвязи. Соответственно, если х и у ъ основном связаны прямо пропорционально, то большинство произведений отклонений будет положительным, а если они связаны обратным соотношением, то большинство произведений будет отрицательным. Следовательно, общим показателем для силы и направления взаимосвязи может служить сумма всех произведений отклонений для данной выборки:

При прямо пропорциональной связи между переменными эта величина является большой и положительной — для большинства испытуемых отклонения совпадают по знаку (большим значениям одной переменной соответствуют большие значения другой переменной и наоборот). Если же х и у имеют обратную связь, то для большинства испытуемых большим значениям одной переменной будут соответствовать меньшие значения другой переменной, т. е. знаки произведений будут отрицательными, а сумма произведений в целом будет тоже большой по абсолютной величине, но отрицательной по знаку. Если систематической связи между переменными не будет наблюдаться, то положительные слагаемые (произведения отклонений) уравновесятся отрицательными слагаемыми, и сумма всех произведений отклонений будет близка к нулю.

Чтобы сумма произведений не зависела от объема выборки, достаточно ее усреднить. Но мера взаимосвязи нас интересует не как генеральный параметр, а как вычисляемая его оценка — статистика. Поэтому, как и для формулы дисперсии, в этом случае поступим так же, делим сумму произведений отклонений не на N, а на N— 1. Получается мера связи, широко применяемая в физике и технических науках, которая называется ковариацией (Covariance):

В психологии, в отличие от физики, большинство переменных измеряются в произвольных шкалах, так как психологов интересует не абсолютное значение признака, а взаимное расположение испытуемых в группе. К тому же ковариация весьма чувствительна к масштабу шкалы (дисперсии), в которой измерены признаки. Чтобы сделать меру связи независимой от единиц измерения того и другого признака, достаточно разделить ковариацию на соответствующие стандартные отклонения. Таким образом и была получена формула коэффициента корреляции К. Пирсона.

Или, после подстановки σ_x и σ_y, получим:

Приведенное выше уравнение является основной формулой коэффициента корреляции Пирсона. Эта формула вполне осмысленна, но не очень удобна для вычислений «вручную» или на калькуляторе. Поэтому существуют производные формулы — более громоздкие по виду, менее доступные осмыслению, но упрощающие расчеты. Мы не будем их здесь приводить, так как один раз в жизни можно в учебных целях посчитать корреляцию Пирсона и по исходной формуле «вручную», а в дальнейшем для обработки реальных данных все равно придется воспользоваться компьютерными программами.

ПРИМЕР

Для расчета коэффициента корреляции воспользуемся данными предыдущего примера о вербальном и невербальном IQ, измеренном у 20 учащихся 8-го класса. К двум столбцам с исходными данными добавляются еще 5 столбцов для дополнительных расчетов, и внизу — строка сумм.

На первом шаге подсчитываются суммы всех значений одного, затем — другого признака для вычисления соответствующих средних значений М_х и М_у: М_х = 9,8; М_у= 10,4.

Далее для каждого испытуемого вычисляются отклонения от среднего: для Х идля Y. Каждое отклонение от среднего возводится в квадрат. В последнем столбике записывается результат перемножения двух отклонений от среднего для каждого испытуемого.

Суммы отклонений от среднего для каждой переменной должны быть равны нулю (с точностью до погрешности вычислений). Сумма квадратов отклонений необходима для вычисления стандартных отклонений по известной формуле

Сумма произведений отклонений дает нам значение числителя, а произведение стандартных отклонений и (N — 1) — значение знаменателя формулы коэффициента корреляции.

Отметим еще раз: на величину коэффициента корреляции не влияет то, в каких единицах измерения представлены признаки. Следовательно, любые линейные преобразования признаков (умножение на константу, прибавление константы: yt = хр + а) не меняют значения коэффициента корреляции. Исключением является умножение одного из признаков на отрицательную константу: коэффициент корреляции меняет свой знак на противоположный.

На рис. 2 приведены примеры диаграмм рассеивания для различных значений коэффициента корреляции. Обратите внимание: на последнем рисунке визуально наблюдается нелинейная взаимосвязь между переменными, однако коэффициент корреляции равен нулю. Таким образом, коэффициент корреляции Пирсона есть мера прямолинейной взаимосвязи; он не чувствителен к криволинейным связям.

РАНГОВЫЙ КОЭФФИЦИЕНТ

КОРРЕЛЯЦИИ СПИРМЕНА

Коэффициент корреляции рангов, предложенный К Спирменом, относится к непараметрическим показателям связи между переменными, измеренными в ранговой шкале При расчете этого коэффициента не требуется никаких предположений о характере распределений признаков в генеральной совокупности Этот коэффициент определяет степень тесноты связи порядковых признаков, которые в этом случае представляют собой ранги сравниваемых величин Правила ранжирования варьирующих величин были описаны выше.

Величина коэффициента линейной корреляции Спирмена также лежит в интервале +1 и -1 Он, как и коэффициент Пирсона, может быть положительным и отрицательным, характеризуя направленность связи между двумя признаками, измеренными в ранговой шкале

В принципе число ранжируемых признаков (качеств, черт и т п ) может быть любым, но сам процесс ранжирования большего чем 20 числа признаков — затруднителен Возможно, что именно поэтому таблица критических значений рангового коэффициента корреляции рассчитана лишь для сорока ранжируемых признаков (n < 40). В случае использования большего, чем 40 числа ранжируемых признаков, уровень значимости коэффициента корреляции следует находить с использованием пакетов прикладных программ.

Ранговый коэффициент линейной корреляции Спирмена подсчитывается по формуле:

.

где n — количество ранжируемых признаков (показателей, испытуемых)

D — разность между рангами по двум переменным для каждого испытуемого

Σ(D²) — сумма квадратов разностей рангов.

КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ

«τ» (тау) КЕНДАЛЛА

Коэффициент корреляции «τ» (тау) Кендалла относится к числу непараметрических, т е при вычислении этого коэффициента не играет роли характер распределения сравниваемых переменных Коэффициент τ предназначен для работы с данными, полученными в ранговой шкале Иногда этот коэффициент можно использовать вместо коэффициента корреляции Спирмена, поскольку способ его вычисления более прост он основан на вычислении суммы инверсий и совпадений.

Таблица возможного использования коэффициентов корреляции приведена ниже.

ЧАСТНАЯ КОРРЕЛЯЦИЯ

Очень часто две переменные коррелируют друг с другом только за счет того, что обе они согласованно меняются под влиянием некоторой третьей переменной. Иными словами, на самом деле связь между соответствующими свойствами отсутствует, но проявляется в статистической взаимосвязи (корреляции) под влиянием общей причины.

ПРИМЕР

Общей причиной изменчивости двух переменных («третьей переменной») может являться возраст при изучении взаимосвязи различных психологических особенностей в группе детей разного возраста. Предположим, что изучается взаимосвязь между зрелостью моральных суждений — Хн скоростью чтения — К . Но в распоряжении исследователя имеется лишь выборка из 45 детей разного возраста — от 8 до 14 лет (переменная Z— возраст). Если будет получена существенная положительная корреляция между Х и У, например r_xy = 0,54, то о чем это будет свидетельствовать? Осторожный исследователь вряд ли сделает однозначный вывод о том, что зрелость моральных суждений непосредственно связана со скоростью чтения. Скорее всего, дело в том, что и зрелость моральных суждений, и скорость чтения повышаются с возрастом. Иными словами, возраст является причиной согласованной (прямо пропорциональной) изменчивости и зрелости моральных суждений, и скорости чтения.

Для численного определения степени взаимосвязи двух переменных при условии исключения влияния третьей применяют коэффициент частной корреляции(Partial Correlation). Для вычисления частной корреляции достаточно знать три коэффициента корреляции /--Пирсона между переменными X, У и Z: r_xy,r_xz и r_yz):

Частная корреляция r_xy-z равна r_xy, при любом фиксированном значении Z (в том случае, если Z линeйнo коррелирует с Х и Y). Например, если значение частной корреляции скорости чтения Х изрелости моральных суждений Ус учетом возраста равно 0,2 (r_xy__z = 0,2) и возраст линейно коррелирует и с Х ис У, то с любой группе детей одного и того же возраста r_xy будет тоже равно 0,2.

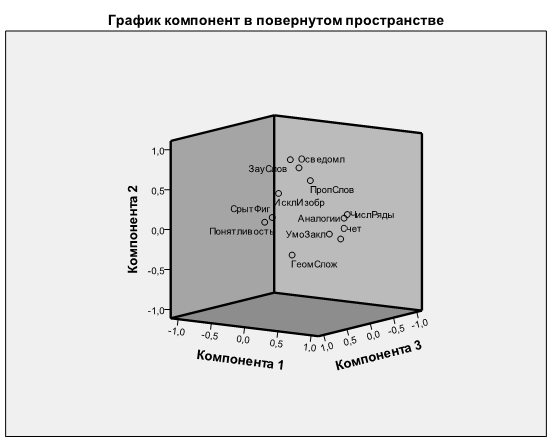
9. ФАКТОРНЫЙ И КЛАСТЕРНЫЙ АНАЛИЗ. ФАКТОРНЫЙ АНАЛИЗ.

Возникновение и развитие факторного анализа тесно связано с измерениями в психологии. Длительное время факторный анализ и воспринимался как математическая модель в психологической теории интеллекта. Лишь начиная с 50-х годов XX столетия, одновременно с разработкой математического обоснования факторного анализа, этот метод становится общенаучным. К настоящему времени факторный анализ является неотъемлемой частью любой серьезной статистической компьютерной программы и входит в основной инструментарий всех наук, имеющих дело с многопараметрическим описанием изучаемых объектов, таких, как социология, экономика, биология, медицина и другие.

Основная идея факторного анализа была сформулирована еще Ф. Гальтоном, основоположником измерений индивидуальных различий. Она сводится к тому, что если несколько признаков, измеренных на группе индивидов, изменяются согласованно, то можно предположить существование одной общей причины этой совместной изменчивости — фактора как скрытой (латентной), непосредственно не доступной измерению переменной. Далее К. Пирсон в 1901 году выдвигает идею «метода главных осей», а Ч. Спирмен, отстаивая свою однофакторную концепцию интеллекта, разрабатывает математический аппарат для оценки этого фактора, исходя из множества измерений способностей. В своей работе, опубликованной в 1904 году, Ч. Спирмен показал, что если ряд признаков попарно коррелируют друг с другом, _ то может быть составлена система линейных уравнений, связывающих все эти признаки, один общий фактор «общей одаренности» и по одному специфическому фактору «специальных способностей» для каждой переменной. В 1930-х годах Л. Терстоун впервые предлагает «многофакторный анализ» для описания многочисленных измеренных способностей меньшим числом общих факторов интеллекта, являющихся линейной комбинацией этих исходных способностей. С 1950-х годов, с появлением компьютеров, факторный анализ начинает очень широко использоваться в психологии при разработке тестов, обоснования структурных теорий интеллекта и личности. При этом исследователь начинает с множества измеренных эмпирических показателей, которые при помощи факторного анализа группируются по факторам (изучаемым свойствам). Факторы получают интерпретацию по входящим в них переменным, затем отбираются наиболее «весомые» показатели этих факторов, отсеиваются малозначимые переменные, вычисляются значения факторов для испытуемых и сопоставляются с внешними эмпирическими показателями изучаемых свойств.

В дальнейшем, по мере развития математического обеспечения факторного анализа, накопления опыта его использования, прежде всего в психологии, задача факторного анализа обобщается. Как общенаучный метод, факторный анализ становится средством для замены набора коррелирующих измерений существенно меньшим числом новых переменных (факторов). При этом основными требованиями являются: а) минимальная потеря информации, содержащейся в исходных данных, и б) возможность представления (интерпретации) факторов через исходные переменные.

Таким образом, главная цель факторного анализа — уменьшение размерности исходных данных с целью их экономного описания при условии минимальных потерь исходной информации. Результатом факторного анализа является переход от множества исходных переменных к существенно меньшему числу новых переменных — факторов. Факторпри этом интерпретируется как причина совместной изменчивости нескольких исходных переменных.

Если исходить из предположения о том, что корреляции могут быть объяснены влиянием скрытых причин — факторов, то основное назначение факторного анализа — анализ корреляций множества признаков.

ПРИМЕР 1

Рассмотрим результаты факторного анализа на простом примере. Предположим, исследователь измерил на выборке из 50 испытуемых 5 показателей интеллекта: счет в уме, продолжение числовых рядов, осведомленность, словарный запас, установление сходства. Все показатели статистически значимо взаимосвязаны на уровне р < 0,05, кроме показателя № 4 с № 1 и 2 (табл. 1).

Таблица 1 Матрица корреляций пяти показателей интеллекта

Таблица 2. Факторные нагрузки после варимакс-вращения

Применив факторный анализ, исследователь выделил два фактора. Основной результат, который подлежит интерпретации исследователем, — таблица факторных нагрузок после варимакс-вращения (табл. 2). Не рассматривая пока шаги, приводящие к этому результату, попытаемся проинтерпретировать полученные данные. В нашем примере по фактору 1 (F_{) максимальные нагрузки имеют переменные 1 и 2. Следовательно, фактор 1 и определяется этими переменными. Поскольку переменная 1 — счет в уме, а переменная 2 — продолжение числового ряда, то фактору 1 может быть присвоено название «арифметические способности», как показателю легкости оперирования числовым материалом. Точно так же фактору 2 можно присвоить название «вербальные способности», как показателю словесного понимания. Нетрудно заметить, что переменные, определяющие фактор, сильнее связаны друг с другом, чем с другими переменными (табл. 16.1). Так, переменные 1 и 2, определяющие фактор 1, сильнее связаны друг с другом, чем с переменными 3, 4 и 5. Таким образом, за взаимосвязью пяти исходных измерений способностей при помощи факторного анализа обнаруживается действие двух латентных переменных (факторов).

Интерпретация фактора через исходные переменные

Интерпретация факторов — одна из основных задач факторного анализа. Ее решение заключается в идентификации факторов через исходные переменные. Эта идентификация и осуществляется по результатам обработки, представленным в табл. 2.

Основное содержание табл. 2 — величины а_и ... а₂$ — факторные нагрузки переменных 1 ... 5 (строки) по факторам 1 и 2 (столбцы). Факторные нагрузки — аналоги коэффициентов корреляции, показывают степень взаимосвязи соответствующих переменных и факторов: чем больше абсолютная величина факторной нагрузки, тем сильнее связь переменной с фактором, тем больше данная переменная обусловлена действием соответствующего фактора. Каждый фактор идентифицируется по тем переменным, с которыми он в наибольшей степени связан, то есть по переменным, имеющим по этому фактору наибольшие нагрузки. Идентификация фактора заключается, как правило, в присвоении ему имени, обобщающего по смыслу наименования входящих в него переменных.

Если исследователя интересует только структура измеренных признаков, на этом факторный анализ завершается. Продолжая факторный анализ, исследователь далее может вычислить значения факторов для испытуемых, например, с целью их дифференциации по преобладанию арифметических или вербальных способностей.

Выбирая факторный анализ как средство изучения корреляций, исследователь должен отдавать себе отчет в том, что это один из самых сложных и трудоемких методов. Зачастую нет веских оснований предполагать наличие факторов как скрытых причин изучаемых корреляции, и задача заключается лишь в обнаружении группировок тесно связанных переменных. Тогда целесообразнее вместо факторного анализа использовать кластерный анализ корреляций (см. ниже). Помимо простоты, кластерный анализ обладает еще одним преимуществом: его применение не связано с потерей исходной информации о связях между переменными, что неизбежно при факторном анализе. И уже после выделения групп тесно связанных переменных можно попытаться применить факторный анализ для их объяснения.

Итак, можно сформулировать основные задачи факторного анализа:

1. Исследование структуры взаимосвязей переменных. В этом случае каждая группировка переменных будет определяться фактором, по которому эти переменные имеют максимальные нагрузки.

2. Идентификация факторов как скрытых (латентных) переменных — причин взаимосвязи исходных переменных.

Вычисление значений факторов для испытуемых как новых, интегральных переменных. При этом число факторов существенно меньше числа исходных переменных. В этом смысле факторный анализ решает задачу сокращения количества признаков с минимальными потерями исходной информации.

КЛАСТЕРНЫЙ АНАЛИЗ

Кластерный анализ решает задачу построения классификации, то есть разделения исходного множества объектов на группы (классы, кластеры). При этом предполагается, что у исследователя нет исходных допущений ни о составе классов, ни об их отличии друг от друга. Приступая к кластерному анализу, исследователь располагает лишь информацией о характеристиках (признаках) для объектов, позволяющей судить о сходстве (различии) объектов, либо только данными об их попарном сходстве (различии). В литературе часто встречаются синонимы кластерного анализа: автоматическая классификация, таксономический анализ, анализ образов (без обучения).

Несмотря на то, что кластерный анализ известен относительно давно (впервые изложен Тгуоп в 1939 году), распространение эта группа методов получила существенно позже, чем другие многомерные методы, такие, как факторный анализ. Лишь после публикации книги «Начала численной таксономии» биологами Р. Сокэл и П. Снит в 1963 году начинают появляться первые исследования с использованием этого метода. Тем не менее, до сих пор в психологии известны лишь единичные случаи удачного применения кластерного анализа, несмотря на его исключительную простоту. Вызывает удивление настойчивость, с которой психологи используют для решения простой задачи классификации (объектов, признаков) такой сложный метод, как факторный анализ. Вместе с тем, как будет показано в этой главе, кластерный анализ не только гораздо проще и нагляднее решает эту задачу, но и имеет несомненное преимущество: результат его применения не связан с потерей даже части исходной информации о различиях объектов или корреляции признаков.

Варианты кластерного анализа — это множество простых вычислительных процедур, используемых для классификации объектов. Классификация объектов — это группирование их в классы так, чтобы объекты в каждом классе были более похожи друг на друга, чем на объекты из других классов. Более точно, кластерный анализ— это процедура упорядочивания объектов в сравнительно однородные классы на основе попарного сравнения этих объектов по предварительно определенным и измеренным критериям.

Существует множество вариантов кластерного анализа, но наиболее широко используются методы, объединенные общим названием иерархический кластерный анализ(Hierarchical Cluster Analysis). В дальнейшем под кластерным анализом мы будем подразумевать именно эту группу методов. Рассмотрим основной принцип иерархического кластерного анализа на примере.

ПРИМЕР .1
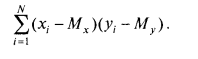
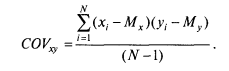
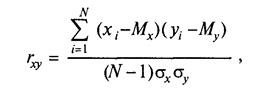
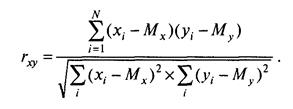
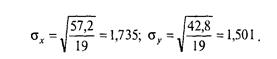