|
|
Н - критерий Крускала-УоллисаНазначение критерия Критерий предназначен для оценки различий одновременно между тремя, четырьмя и т.д. выборками по уровнюкакого-либо признака. Он позволяет установить, что уровень признака изменяетсяпри переходе от группы к группе, но не указывает на направление этих изменений. Описание критерия Критерий Н иногда рассматривается как непараметрический аналог метода дисперсионного однофакторного анализа для несвязных. Данный критерий является продолжением критерия U на большее, чем 2, количество сопоставляемых выборок. Все индивидуальные значения ранжируются так, как если бы это была одна большая выборка. Затем все индивидуальные значения возвращаются в свои первоначальные выборки, и мы подсчитываем суммы полученных ими рангов отдельно по каждой выборке. Если различия между выборками случайны, суммы рангов не будут различаться сколько-нибудь существенно, так как высокие и низкие ранги равномерно распределятся между выборками. Но если в одной из выборок будут преобладать низкие значения рангов, в другой - высокие, а в третьей - средние, то критерий Н позволит установить эти различия. Гипотезы H0: Между выборками 1, 2, 3 и т. д. существуют лишь случайные различия по уровню исследуемого признака.
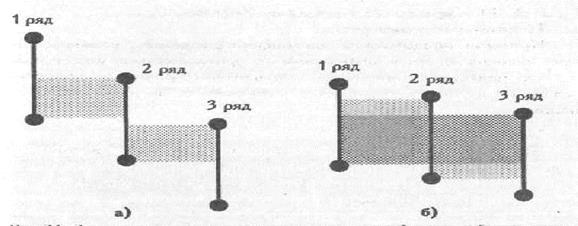
H1: Между выборками 1, 2, 3 и т. д. существуют неслучайные различия по уровню исследуемого признака. Графическое представление критерия Н Критерий Н оценивает общую сумму перекрещивающихся зон при сопоставлении всех обследованных выборок. Если суммарная область наложения мала (Рис. 2.6 (а)), то различия достоверны; если она достигает определенной критической величины и превосходит ее (Рис. 2.6 (б)), то различия между выборками оказываются недостоверными.
Рис.6. 2 возможных варианта соотношения рядов значений в трех выборках; штриховкой отмечены зоны наложения Ограничения критерия Н
При сопоставлении 3-х выборок допускается, чтобы в одной из них n=3, а двух других п=2. Но при таких численных составах выборок мы сможем установить различия лишь на низшем уровне значимости (Р≤0,05). Для того, чтобы оказалось возможным диагностировать различия на более высоком уровнем значимости (р≤0,01), необходимо, чтобы в каждой выборке было не менее 3 наблюдений, или чтобы по крайней мере в одной из них было 4 наблюдения, а вдвух других - по 2; при этом неважно, в какой именно выборке сколько испытуемых, а важно соотношение 4:2:2. Критические значения критерия Н и соответствующие им уровни значимости приведены в Табл. IV Приложения 1. Таблица предусмотрена только для трех выборок и (n1, n2, n3)≤5. При большем количестве выборок и испытуемых в каждой выборке необходимо пользоваться Таблицей критических значений критерия χ2, поскольку критерий Крускала-Уоллиса асимптотически приближается к распределению χ 2 (Носенко И.А., 1981;J. Greene, M. DOlivera, 1982). Количество степеней свободы при этом определяется по формуле: v=c-l где с - количество сопоставляемых выборок.
Пример В эксперименте по исследованию интеллектуальной настойчивости (Е.В. Сидоренко, 1984) 22 испытуемым предъявлялись сначала разрешимые четырехбуквенные, пятибуквенные и шестибуквенные анаграммы, а затем неразрешимые анаграммы, время работы над которыми не ограничивалось. Эксперимент проводился индивидуально с каждым испытуемым. Использовалось 4 комплекта анаграмм. У исследователя возникло впечатление, что над некоторыми неразрешимыми анаграммами испытуемые продолжали работать дольше, чем над другими, и, возможно, необходимо будет делать поправку на то, какая именно неразрешимая анаграмма предъявлялась тому или иному испытуемому. Показатели длительности попыток в решении неразрешимых анаграмм представлены в Табл. 2.5. Все испытуемые были юношами-студентами технического вуза в возрасте от 20 до 22 лет. Можно ли утверждать, что длительность попыток решения каждой из 4 неразрешимых анаграмм примерно одинакова? Таблица 5 Показатели длительности попыток решения 4 неразрешимых анаграмм в секундах (N=22)
Сформулируем гипотезы.
Н0: 4 группы испытуемых, получившие разные неразрешимые анаграммы, не различаются по длительности попыток их решения. H1: 4 группы испытуемых, получившие разные неразрешимые анаграммы, различаются по длительности попыток их решения. Теперь познакомимся с алгоритмом расчетов. АЛГОРИТМ |
|
3. При множественном сопоставлении выборок достоверные различия между какой-либо конкретной парой (или парами) их могут оказаться стертыми. Это ограничение можно преодолеть, если провести все возможные попарные сопоставления,число которых будет равняться ½*[c*(c-1)]*1. Для таких попарных сопоставлений используется, естественно, критерий для двухвыборок, например U или φ*.