|
|
Обозначения в структурных схемахЭлементы систем автоматического управления в структурных схемах принято изображать в следующем виде: 1. Звено обозначают в виде прямоугольника, с указанием входного и выходного параметров, например:
Рис.54. Условное изображение звена в структурной схеме
Для удобства внутри прямоугольника может быть указана передаточная функция. Допускается вместо W(р) указывать уравнение или характеристику звена. Обозначения входных и выходных параметров записывают в виде изображений или оригиналов в зависимости от обозначения в прямоугольнике. Допускается нумерация звеньев и представление их передаточных функций, уравнений или характеристик вне схемы. 2. Канал передачи сигнала изображается линией со стрелкой, указывающей направление прохождения сигнала. 3. Сравнивающие элементы изображаются в следующем виде:
Рис.55. Условное изображение сравнивающего элемента: а) у = х1 + х2 б) у = х1 - х2
Правила преобразования структурных схем
Типовыми соединениями звеньев являются: последовательное, параллельное и соединение с обратной связью, представленные ниже:
Рис.56. Схемы соединения звеньев: а – последовательное; б – параллельное; в – с обратной связью
При последовательном соединении звеньев выходная величина предыдущего звена является входной величиной последующего звена (рис.56 а). Передаточная функция системы последовательно соединенных звеньев равна произведению передаточных функций отдельных звеньев:
АФЧХ системы будет равна произведению АЧФХ отдельных звеньев:
В случаях, когда АФЧХ записаны в показательной форме, для получения модуля АФЧХ системы необходимо перемножить модули отдельных звеньев, а для получения фазы АФЧХ системы необходимо сложить фазы отдельных звеньев:
При наличии параллельного соединения звеньев (рис.56 б) на вход всех звеньев поступает одна и та же входная величина Передаточная функция системы при параллельном соединении звеньев равна сумме передаточных функций отдельных звеньев:
АФЧХ системы при параллельном соединении звеньев равна сумме АФЧХ отдельных звеньев:
В случаях, когда звено с передаточной функцией W1(p) охвачено обратной связью от звена с передаточной функцией Woc(p) (рис.56 в), соблюдаются соотношения:
Положительная обратная связь — связь, с введением которой увеличивается выходная величина, а отрицательная связь — связь, с введением которой выходная величина уменьшается по сравнению со значением без обратной связи. Знак «+» в структурной схеме указывает на наличие положительной обратной связи, а знак «—» - отрицательной. Осуществив переход функций от их оригиналов к изображениям в выражении (2.13.) и разделив полученные изображения на изображение выходного параметра Xвых(p), получим:
В левой части выражения находится представление обратной передаточной функции основного звена. Первое слагаемое правой части выражения — обратная передаточная функция всей системы, а второе слагаемое правой части выражения представляет собой передаточную функцию звена обратной связи, т.е. выражение можно записать, как:
Для получения передаточной функции системы с обратной связью преобразуем выражение и получим:
причем знак «+» соответствует отрицательной обратной связи, а знак «—» - положительной обратной связи. АФЧХ системы с обратной связью будет иметь вид:
Пример преобразования структурной схемы
Необходимо найти передаточную функцию системыW (р), структурная схема которой представлена на рисунке 57.
Рис.57. Структурная схема САУ
Решение:
Применяя формулы (2.8.) и (2.11.) для последовательного и параллельного соединений звеньев, получим следующее выражение передаточной функции системы:
W (р) = W1(р)W2 (р) [W3(р) −W4 (р)] W5 (р) (2.18.)
|
|



 (2.8.)
(2.8.) . (2.9.)
. (2.9.) (2.10.)
(2.10.) , а выходная величина равна сумме выходных величин отдельных звеньев:
, а выходная величина равна сумме выходных величин отдельных звеньев:  .
.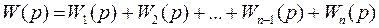 (2.11.)
(2.11.) (2.12.)
(2.12.)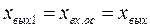 ;
;  . (2.13.)
. (2.13.)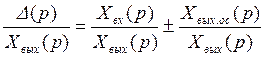 (2.14.)
(2.14.) (2.15.)
(2.15.) (2.16.)
(2.16.) (2.17.)
(2.17.)