|
|
Интегральные показатели качества регулированияИнтегральные показатели качества регулирования являются обобщенными показателями качества, и в отличие от прямых и косвенных показателей, интегральные показатели характеризуют не одно какое-либо свойство системы, а совокупность свойств. Для наглядности представим интегральный показатель качества в следующем виде:
где f(x) – функция всех переменных, характеризующих свойства системы. При анализе качества регулирования системы по задающему воздействию с использованием переходной функции h(t )используют понятиелинейной интегральной оценки, которая выражается, как:
Геометрически данную оценку можно выразить в виде площади, ограниченной прямой у = h(∞) и графиком переходной функции h(t ). Линейная интегральная оценка учитывает не только значения динамических изменений управляемого параметра, но и длительность этих изменений, а значит, чем меньше значение оценки, тем лучше качество регулирования системы. Примем за δ (∞) – установившуюся ошибку системы, за уз – задающее воздействие и получим значение:
h(∞) = уз - δ (∞) (2.96.)
Совершив необходимое преобразование, получим следующее выражение:
h(∞) − h(t) = yз −δ(∞) − h(t) = yз − h(t) −δ(∞) = δ(t) −δ(∞) (2.97.) Исходя из полученного выражения, линейную интегральную оценку можно представить в виде:
Графическое представление линейной интегральной оценки качества регулирования по задающему воздействию изображено на рисунке 91.
Рис.91. Графическое представление линейной интегральной оценки качества регулирования по задающему воздействию
Линейная интегральная оценка при анализе качества регулирования системы по возмущающему воздействию определяется с помощью импульсной переходной функции w(t ) и выражается в виде:
Рассмотренные линейные интегральные оценки качества регулирования подходят только для анализа процессов, выраженных в монотонной форме, поэтому наиболее часто применяют квадратичную интегральную оценку, которая подходит и для колебательных процессов. Квадратичная интегральная оценка не зависит от знака δ(t) ивыражается подобным образом:
Рассмотрим метод, с помощью которого возможно определение квадратичной интегральной оценки, без решения характеристического уравнения. С учетом того, что
и проинтегрировав │δ( jω)│2 по ω, получим следующее выражение квадратичной интегральной оценки:
Для того, чтобы полнее учесть влияние величины ошибки и скорости ее изменения применяют интегральную оценку по скорости, которая выражается в следующем виде:
γ – является весовым коэффициентом, указывающим на значимость интегрируемой производной функции. Кроме интегральной оценки по скорости, в некоторых случаях применяют интегральную оценку качества регулирования по ускорению, которая выражается, как:
где γ1, γ2 – весовые коэффициенты, указывающие на значимость интегрируемых производных функций. Все вышеперечисленные интегральные оценки качества регулирования САУ могут быть приведены к необходимым численным значениям путем изменения параметров системы, т.к. данные оценки напрямую зависят от свойств САУ.
Контрольные тесты к разделу 2: «ЭЛЕМЕНТЫ СИСТЕМ АВТОМАТИКИ, ЭЛЕМЕНТЫ АНАЛИЗА И СИНТЕЗА СИСТЕМ УПРАВЛЕНИЯ»
По разомкнутой системе судят об устойчивости замкнутой в критерии а) Найквиста б) Гурвица в) Михайлова г) Рауса
Критерий Гурвица является а) интегральным б) частотным в) корневым г) алгебраическим
Кривая Михайлова строится а) по характеристическому уравнению системы б) по комплексному коэффициенту передачи системы в) по передаточной функции системы г) по нулям и полюсам передаточной функции
Условия, позволяющие оценить положение полюсов системы на комплексной плоскости без вычисления их значений, это а) степень устойчивости б) показатели качества в) критерии устойчивости г) способы нормирования
Число строк таблицы Рауса равно а) n+1 б) n-1 в) порядку системы n г) произвольной величине
|
|
 (2.94.)
(2.94.)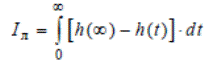 (2.95.)
(2.95.) (2.98.)
(2.98.)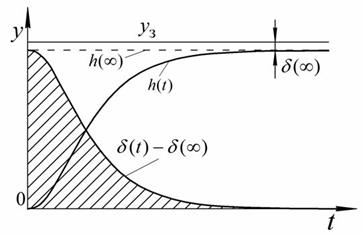
 (2.99.)
(2.99.)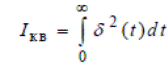 (2.100.)
(2.100.) (2.101.)
(2.101.) (2.102а.)
(2.102а.) (2.102б.)
(2.102б.) (2.103.)
(2.103.) (2.104.)
(2.104.)