|
|
Качество процесса управления САУ в переходном режиме
В переходном режиме величины параметров не имеют какого-либо установившегося значения, поэтому точность регулирования определяют в виде совокупности некоторого количества мгновенных значений ошибки δ (t), которые образуются при подаче ступенчатого воздействия 1(t) в виде величины задающих и возмущающих параметров. Различают прямые и косвенные показатели качества регулирования, которые относят к различным группам, соответственно способу их определения. Прямые показатели качества могут быть определены с помощью временных характеристик – переходной функции h(t)по входным параметрам или импульсной переходной функции w(t) по параметрам внешнего воздействия. При анализе качества регулирования большое значение уделяют форме переходного процесса, представленной на рисунке 87, которая в общем случае может быть: а) колебательной, б) апериодической, в) монотонной.
Рис.87. Графики переходной функции h(t)и импульсной переходной функции w(t) в зависимости от формы переходного процесса Рассмотрим определение прямых показателей качества для колебательного процесса, т.к. именно для данного процесса количество прямых показателей является наибольшим. На рисунке 88 представлены основные показатели колебательного процесса.
Рис.88. Графическое представление основных показателей колебательного процесса
Основными показателями переходной функции h(t)в колебательном переходном процессе являются перерегулирование σи время регулирования tр. Как уже отмечалось ранее в п. 2.1.1., перерегулированием называется максимальное отклонение регулируемой величины параметра от установившейся величины параметра. Например, для рассматриваемого случая перерегулирование будет выражаться в следующем виде:
Величина перерегулирования может устанавливаться в зависимости от характера применения и типа САУ (см. 2.1.1.). Временем регулирования tр – называется время, за которое система приходит в состояние, когда величина переходной функции h(t)попадает в полосу и остается в полосе пропускания (см.2.1.1.), ширина которой составляет ±5% от установившегося значения параметра. Время регулирования характеризует инерционность системы, т.е. время протекания переходного процесса. В случае, когда имеет место монотонная форма переходного процесса, время регулирования является единственным показателем качества регулирования. К дополнительным показателям качества регулирования можно отнести: - время, за которое значение переходной функции первый раз достигает номинального значения, на рисунке 88 обозначено tпс. - частоту колебаний ω = 2π /T, - количество колебаний nк , произведенное за время регулирования tр, - степень затухания ψ (подробнее см. стр. 47.) - время, за которое значение переходной функции достигает своего максимума tmax. Считается, что необходимое качество регулирования САУ достигнуто, если значения переходной функции за время переходного процесса не выходят из полосы пропускания, и показатели качества регулирования соответствуют заданным. Графическое представление данных условий изображено на рисунке 89.
Рис.89. Графическое представление границ необходимого качества регулирования
Среди косвенных показателей качества регулирования различают: - корневые показатели, - частотные показатели, - интегральные показатели. Рассмотрим корневые показатели качества регулирования. Переходной процесс в системе характеризуется ее передаточной функцией W(р). В случае, когда в числителе переходной функции отсутствуют нули, система характеризуется полюсами, т.е. корнями характеристического уравнения системы A(р). На комплексной плоскости можно обозначить область расположения корней данного уравнения при A(р) = 0, которая чаще всего принимает форму трапеции, на сторонах и основании которой располагаются корни, как изображено на рисунке 90.
Рис.90. Область расположения корней характеристического уравнения
Чем ближе расположение корней уравнения к мнимой оси, тем медленнее процесс затухания. Действительной частью этих корней определяется степень устойчивости α. Колебательность системы μ имеет основное влияние на переходной процесс и рассчитывается так же, как степень колебательности колебательного звена (см. стр.47.). По величине μ можно судить о количестве колебаний nк , произведенных за время регулирования и о величине перерегулирования σ, т.к. с увеличением колебательности увеличиваются значения nк и σ. При условии, что пара комплексно-сопряженных корней уравнения расположена ближе остальных корней к мнимой оси на комплексной плоскости, по величине колебательности μ определяют приближенное значение перерегулирования, пользуясь следующим выражением: σ ≤e−π / μ (2.89.)
|
|


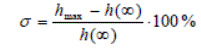 (2.88.)
(2.88.)
