|
|
Основные типы функций принадлежностиЛекция 1. Основные понятия теории нечетких множеств Нечеткое множество(fuzzy set) – представляет собой совокупность элементов произвольной природы относительно которых нельзя с полной определенностью утверждать, принадлежит ли тот или иной элемент рассматриваемой совокупности данному множеству или нет. Формально нечеткое множество А определяется как множество упорядоченных пар или кортежей вида: где
При этом значение В общем случае нечеткое множество записывается
Нечеткие множества обозначаются рукописными прописными буквами, четкие множества – обычными (печатными). Пустое нечеткое множество - множество, которое не содержит ни одного элемента, т.е. функция принадлежности для каждого элемента универсального множества тождественно равно нулю. Единичное нечеткое множество или универсальное множество - принято считать, что функция принадлежности для каждого элемента универсального множества тождественно равна единице. Носитель нечеткого множества – обычное множество, которые содержит те элементы универсального множества для которых значение функции принадлежности отличны от нуля. Математически он обозначается : Конечное нечеткое множество: если носитель множества является конечным, множество конечно. Конечное нечеткое множество имеет конечную мощность, которая численно равна количеству элементов носителя. Бесконечное нечеткое множество – носитель, которого не является конечным множеством. При этом выделяют несколько видов: Счетное нечеткое множество – нечеткое множество, элементы которого можно сосчитать. В случае если универсальное множество непрерывно, то мы имеем дело с несчетным нечетким множеством. Нечеткие множества могут быть заданы двумя способами: · В форме списка с явным перечислением всех элементов · Аналитически в форме математического выражения функции принадлежности Пример : Построить нечеткое множество, которое описывало бы выходные (нерабочие) дни обычной семидневной недели. Рассматриваемое нечеткое множество А описывающее выходные дни недели, может быть задано, например, в виде: А={<понедельник, 0>. <вторник, 0>, <среда, 0>, <четверг, 0>, <пятница, 0.5>, <суббота. 1.0>, <воскресенье, 0.8>} Рис. 1 Графическое представление бесконечного нечеткого множества А. Описывающего выходные дни недели, в форме кривой его функции принадлежности. Рис. 2. Графическое представление обычного множества выходных дней А в форме значений соответствующей характеристической функции. Нечеткое множество обозначает не вероятность, а степень достоверности, с которой элемент нечеткого множества может быть отнесен к данному множеству.
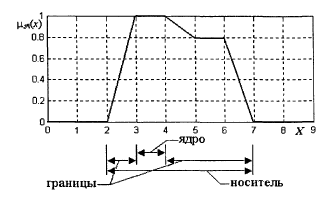
Основные характеристики нечеткого множества: 1. Нечеткое множество альфа уровня Под множеством альфа уровня понимается обычное множество, удовлетворяющее следующему условию
2. Высота нечеткого множества
Нормальное нечеткое множество Если высота нечеткого множества равна единице Субнормальное нечеткое множество Если высота нечеткого множества меньше единицы 3. Ядро нечеткого множества - называется обычное множество, для которого выполняется условие:
4. Границы нечеткого множества Такие элементы универсума для которых значения функции принадлежности отличны от нуля и единиц
Рис. 3. Ядро, носитель и границы нечеткого множества
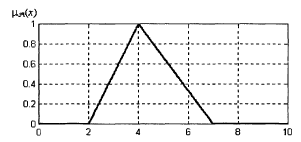
Основные типы функций принадлежности Наиболее простыми видами функций принадлежности является кусочно-линейные функции принадлежности. Наиболее характерным примером этих функций является треугольная и трапециевидная. Треугольная функция принадлежности:
Где a, b и c некоторые числовые параметры a
Рис. 4. График треугольной функции принадлежности
|
|
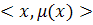
 – является элементом некоторого универсального множества или универсума
– является элементом некоторого универсального множества или универсума 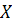 , а
, а 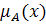 - функция принадлежности, которая ставит в соответствие каждому из элементов
- функция принадлежности, которая ставит в соответствие каждому из элементов 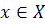 , (где
, (где 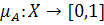
 означает, что элемент
означает, что элемент 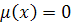 - элемент
- элемент 




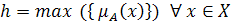
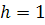
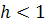


 b
b  c
c