|
|
Автоматическое построение лингвистических переменныхЕсли заранее сказать что-либо о предметной области сложно, универсальное множество разбивается на равные отрезки, число точек разбиения равняется числу термов. Желательно, число термов брать нечетным. Минимальное число термов - 3. Для автоматического построения используют треугольные функции принадлежности Автоматическое построение удобно тем, что оно может быть легко дополнено с помощью последовательного итерационного наращивания лингвистической переменной. Необходимо определить уровень детализации ЛП(t, n) , где t - непосредственно уровень детализации, n - число термов, на данном уровне детализации ЛП(1, 3) - самая простая лингвистическая переменная первого уровня содержит 3 терма. Изменение уровня детализации может производиться автоматически. Условия: · Необходимо сохранять все созданные правила при переходе от первого уровня к следующему, т.е. имена термов изменяться не должны, функция принадлежности термов должна изменяться минимально. · Переход между уровнями должен быть максимально простым и понятным Для построения ЛП уровня t+1 из ЛП уровня t с минимальными изменениями в базе правил и терм – множествах необходимо добавить новые термы только между двумя соседними термами ЛП уровня t ЛП(t, n) →ЛП(t+1, 2*П-1) Число термов 1 уровня соотносится с числом t-го уровня П(t)=(П(1)-1)* При таком подходе существующие правила не меняют лингвистических значений. Понятие нечеткого высказывания Элементарное нечеткое высказывание – повествовательное предложение, выражающее законченную мысль. Мы можем судить о истинности или ложности только с некоторой степенью уверенности Примеры: Иванов имеет высокий рост 3- маленькое число ВАЗ2110 – скоростное авто Неопределенность оценки истинности связана с нечеткостью определений базовых понятий: высокий рост, малое число, скоростной автомобиль
Логическая конъюнкция нечетких высказываний Конъюнкцией нечетких высказываний A и В (записывается как:A T(A T(A Логическую конъюнкцию нечетких высказываний также называют нечетким логическим "И", нечеткой конъюнкцией или min-конъюнкцией и иногда записывают также в формеA AND B. При этом исторически принято считать формулы (1-2) основной для определения степени истинности ее результата.
Нечеткая импликация: Нечеткой импликацией или просто — импликацией нечетких высказываний A и В (записывается как A T(A Классическая импликация T(A) ≥ T(B), тогда: T(A Нечеткая импликация играет важная роль в процессе нечетких рассуждений также как математическая логика. 1 операнд называется предпосылкой или антецедентом , 2 операнд – заключение или консеквент. Пример Нечеткое высказывание, заданное в форме импликации «Если О.Бендер имеет довольно высокий рост, то завтра будет пасмурная погода» T(A) =0.7 T(B) =0.2 T(A
Правила нечетких продукций Под правилом нечеткой продукции понимают выражение следующего вида: Q; P; A => B; S; F; N Где Q - сфера применения нечеткой продукции P- условие применимости нечеткой продукции A => B - ядро нечеткой продукции в котором A - условие ядра или антецедент B - заключение ядра или консеквент => - знак логической консеквенции или следования S - метод определения количественного значения степени истинности заключения ядра F - коэффициент определенности нечеткой продукции N - постусловие продукции Более привычно ядро продукции записывается в форме ЕСЛИ А ТО В, где А и В – нечеткие высказывания
Четкие правила Четкие правила, так же как и нечеткие, состоят из двух частей. Часть условие или антецедент содержит комбинации различных условий (подусловий) объединенных чаще всего логической конъюнкцией (И) реже дизъюнкцией (ИЛИ) В простейшем случае заключение (consequent) осуществляет выбор одного из заранее заданных классов. Пример: Правило выглядит следующим образом: ЕСЛИ (задолженность = «нет») И (остаток_на_счете > 3000$) ТО (кредитное доверие = «хорошо»)
В случае, если задачи классификации в явном виде не наблюдается, к ней можно перейти из произвольной задачи. Простейший способ закодировать интервал - представить его в виде двоичной последовательности Семейное_состояние = Холост/Не замужем Женат/замужем Разведен(а) Овдовел(а) Кодируется 4 битами Например 0110 будет выглядеть ЕСЛИ (семейное_состояние «женат» или «разведен»), Части правила в данном случае объединяются с помощью логической функции «ИЛИ». Для кодирования непрерывных величин можно использовать интервальный подход Пример: Переменная возраст Младенчество 0-3 Детство 4-10 Юность 11-17 Молодость 18-29 Зрелость 30-49 Старость 50-100 ЕСЛИ(11<=возраст<=17) или (18<=возраст<=29) В таком случае одна часть условия кодируется одним двоичным числом, каждый бит двоичного числа представляет собой интервал(четкий интервал). В случае квантования непрерывных переменных границы интервала поменять нельзя Более сложным случаем кодирования интервала является кодирование границ интервала непосредственно в самом условии ЕСЛИ (возраст > 21) и (возраст < 25) Все вышесказанное касается в основном кодирования части условия, хотя может быть применено и для кодирования части заключение
|
|
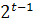 +1
+1 B) называется бинарная логическая операция, результат которой является нечетким высказыванием, истинность которого определяется по формуле:
B) называется бинарная логическая операция, результат которой является нечетким высказыванием, истинность которого определяется по формуле: B)= max(T(A), T(B)) (2)
B)= max(T(A), T(B)) (2) B и читается — "из A следует В", "ЕСЛИ A, ТО В") называется бинарная логическая операция, результат которой является нечетким высказыванием, истинность которого может принимать значение, определяемое по следующей формуле.
B и читается — "из A следует В", "ЕСЛИ A, ТО В") называется бинарная логическая операция, результат которой является нечетким высказыванием, истинность которого может принимать значение, определяемое по следующей формуле.