|
|
Некоторые дополнительные операции над нечеткими множествамиКонцентрирование Пусть на универсуме X задано произвольное нечеткое множество A={x,
Соответствует лингвистическому модификатору «очень»
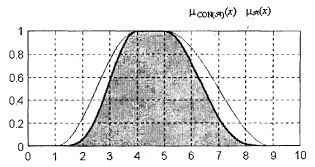
Рис. 19. Графическое представление операции концентрирования нечеткого множества, для П-образной функции принадлежности
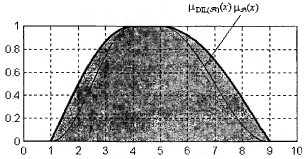
Растяжение Операция растяжения, обозначаемая через DIL(А), дает в результате нечеткое множество A={x, Соответствует лингвистическому модификатору «слегка»
Рис. 20. Графическое представление операции растяжения нечеткого множества, для П-образной функции принадлежности Отрицание Пусть на универсуме X задано произвольное нечеткое множество A={x,
Соответствует лингвистическому модификатору «не»
Лекция 3. Нечеткие операторы Треугольная норма (Т-норма, t-норма) Произвольная действительная функция от двух переменных Т: [0,1]x[0,1]
Типичной Т-нормой является операция взятия минимума (пересечения) двух нечетких множеств. Также условия Т-норм выполняются для алгебраического произведения двух нечетких множеств, граничного произведения (норма Лукасевича) и драстического произведения. Треугольная конорма (Т-конорма, s-норма) Произвольная действительная функция от двух переменных S: [0,1]x[0,1]
Типичной треугольной конормой является операция логической суммы (объединения) двух нечетких множеств. Так же условия Т-конорм выполняются для алгебраической суммы, граничной суммы и драстической суммы. t-норма и t-конорма играют важную роль в ряде приложений, связанных с нечеткими выводами, системами управления и т.д. Чаще всего используют логические произведение и сумму.
Импликатор Импликатором I называется бинарная функция, частные функции которой изменяют порядок по первой переменной, сохраняют по второй, и для которой выполняются условия
Нечеткие высказывания и операции над ними. Нечеткое высказывание Значение 0 соответствует ложности высказывания, 1 – истинности высказывания, 0.5 – индифферентности. Пример. «2 – маленькое число» - Нечеткое высказывание, степень истинности которого может быть равна 0.9. Отрицанием нечеткого высказывания Конъюнкцией нечеткоих высказываний
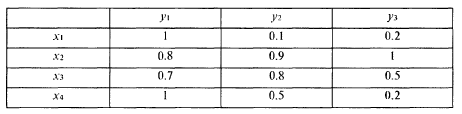
Нечеткие отношения Нечетким отношением называется некоторое фиксированное нечеткое подмножество, заданное на декартовом произведении нескольких универсумов. Пример Необходимо построить некое нечеткое отношение, описывающее поиск неисправности в автомобиле. В качестве первого универсума будем считать множество причин неисправности X={x1, x2, x3, x4} Где x1 - неисправность аккумулятора x2 - неисправность карбюратора x3 – неисправность, связанная с плохим бензином x4 - неисправность системы зажигания В качестве второго универсума рассмотрим множество проявлений неисправностей Y={y1,y2,y3 } Где y1 - двигатель не запускается y2 - двигатель работает неустойчиво y3 - двигатель не развивает общей мощности Причинная взаимосвязь между x и y не является однозначной. Нечеткое отношение может быть представлено следующей таблицей:
Такое нечеткое отношение может быть записано в форме списка:
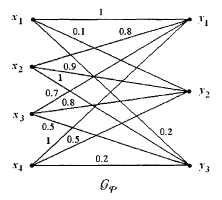
Или в виде нечеткого графа:
|
|
 } - Операция концентрирования, обозначаемая через CON(A), дает в результате нечеткое множество С={x,
} - Операция концентрирования, обозначаемая через CON(A), дает в результате нечеткое множество С={x,  }, функция принадлежности которого равна значениям функции принадлежности исходного нечеткого множества, возведенным в квадрат, т. е.
}, функция принадлежности которого равна значениям функции принадлежности исходного нечеткого множества, возведенным в квадрат, т. е.
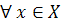
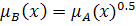
 [0,1] называется треугольной Т-нормой если она удовлетворяет следующим свойствам, называемым аксиомами треугольной нормы:
[0,1] называется треугольной Т-нормой если она удовлетворяет следующим свойствам, называемым аксиомами треугольной нормы:


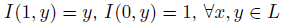
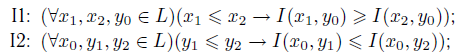

 – повествовательное предложение, относительно которого можно судить о степени его истинности или ложности в настоящее время. Степень истинности d(
– повествовательное предложение, относительно которого можно судить о степени его истинности или ложности в настоящее время. Степень истинности d(  , степень истинности которого определяется выражением
, степень истинности которого определяется выражением  , где N – инвертор.
, где N – инвертор.