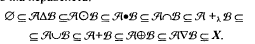|
|
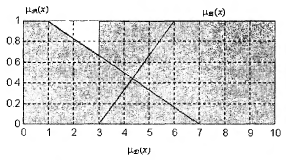
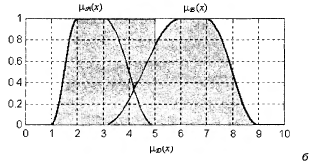
Лекция 2. Операции над нечеткими множествамиРавенство нечетких множеств Два нечетких множества
Равенство множеств в данном случае записывается как A=B Нечеткое подмножество Нечеткое множество t wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>x</m:t></m:r><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>)</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> Записывается так: A Можно сказать, что нечеткое множество В доминирует над нечетким множеством А, а множество А содержится в нечетком множестве В. Если
То говорят о строгом доминировании
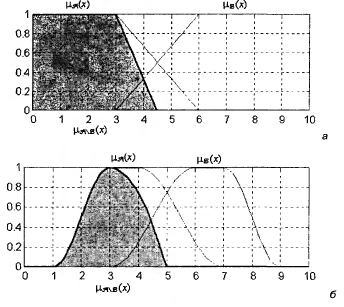
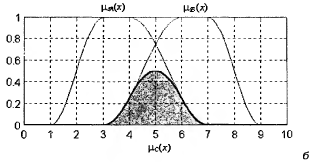
Пересечение Пересечением двух нечетких множеств
Операция пересечения обозначается C= A
Рис. 10. Графическое представление операции пересечения двух нечетких множеств Объединение Объединением двух нечетких множеств
Операция пересечения обозначается C= A
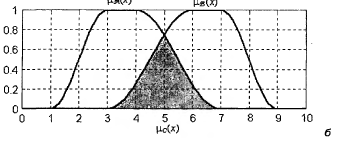
Рис. 11. Графическое представление операции объединения двух нечетких множеств Разность Разностью двух нечетких множеств
Записывается так: C = A - B
Рис. 11. Графическое представление операции разности двух нечетких множеств
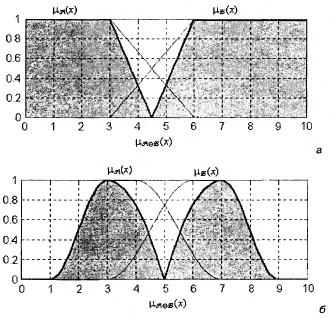
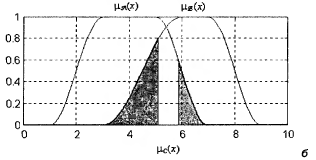
Симметрическая разность Следует заметить, что операция разности двух нечетких множеств в отличие от операций объединения и пересечения не является коммутативной. По аналогии с обычными множествами иногда оказывается полезной операция симметрической разности двух нечетких множеств
Рис. 12. Графическое представление операции симметрической разности двух нечетких множеств
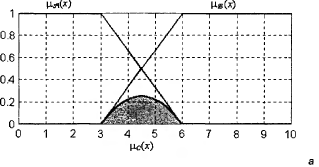
Алгебраическое пересечение Алгебраическим пересечением или алгебраическим дополнением двух нечетких множеств
т. е. как результат обычного арифметического произведения соответствующих значений функций принадлежности.
Рис. 13. Графическое представление операции алгебраического пересечения двух нечетких множеств
Алгебраическое пересечение двух нечетких множеств
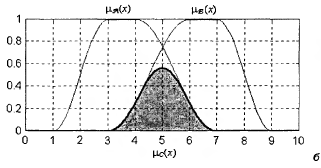
Алгебраическое объединение Алгебраическим объединением двух нечетких множеств
Записывается так: C = A + B
Рис. 14. Графическое представление операции алгебраического объединения двух нечетких множеств Операции алгебраического объединения и пересечения используются не очень часто, т.к. для них выполняются не все из свойств которые описаны в дискретной математике Коммутативность – A Ассоциативность – A Дистрибутивность – A Законы де Моргана – Которые выполняются для классических операций объединения и пересечения.
Граничное пересечение Граничным пересечением двух нечетких множеств
Записывается так: C = A
Рис. 14. Графическое представление операции граничного пересечения двух нечетких множеств
Граничное объединение Граничным объединением двух нечетких множеств
Записывается так: C = A
Рис. 15. Графическое представление операции граничного объединения двух нечетких множеств
Драстическое пересечение Драстическим пересечением(от англ. – решительный, радикальный) двух нечетких множеств
Записывается так: C = A
Рис. 16. Графическое представление операции драстического пересечения двух нечетких множеств
Драстическое объединение Драстическим объединением(от англ. – решительный, радикальный) двух нечетких множеств
Записывается так: C = A
Рис. 17. Графическое представление операции драстического объединения двух нечетких множеств
Операция Эта операция для двух нечетких множеств
Записывается так: C = A
Рис. 18. Графическое представление операции
При этом оказывается справедливой следующая цепочка неравенств:
|
|
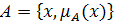 и
и 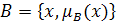 их равенство выполняется, если их функции принадлежности принимают равные значения на всем универсуме X:
их равенство выполняется, если их функции принадлежности принимают равные значения на всем универсуме X:
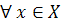
 тогда и только тогда, когда значения функции принадлежности первого не превосходят соответствующих значений функции принадлежности второго, т. е. выполняется следующее условие:
тогда и только тогда, когда значения функции принадлежности первого не превосходят соответствующих значений функции принадлежности второго, т. е. выполняется следующее условие:
 B
B
 и B будем называть некоторое третье нечеткое множество С, заданное на этом же универсуме X. функция принадлежности которого определяется по следующей формуле:
и B будем называть некоторое третье нечеткое множество С, заданное на этом же универсуме X. функция принадлежности которого определяется по следующей формуле:
 B или C= A
B или C= A  B
B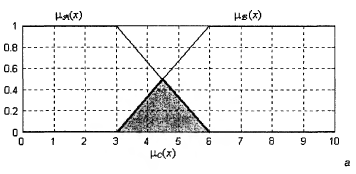

 B или C= A
B или C= A  B
B

 B). По определению:
B). По определению:

 B
B



 C
C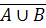 =
= 
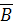 и
и 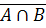 =
= 
 B
B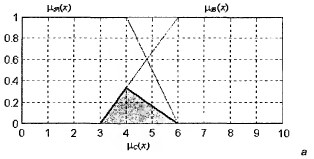

 B
B

 B
B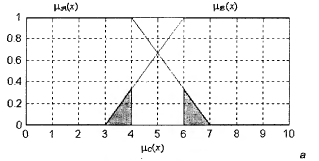

 B
B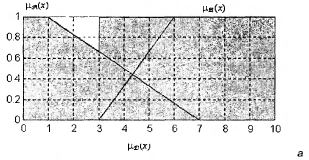
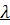 - суммы
- суммы


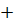 λB
λB