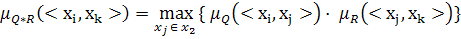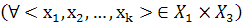|
|
Операции над нечеткими отношенииямиПересечение ( Пересечением двух нечетких отношений Q = {<x1 x2, …, xk> | R = {<x1 x2, …, xk> |
Объединение ( Объединением двух нечетких отношений
Разность ( Разностью двух нечетких отношений
Симметрическая разность ( Симметрической разностью двух нечетких отношений
Композиция бинарных нечетких отношений Пусть Композицией
Определенную таким образом композицию нечетких отношений называют (max-min-)-композицией или максиминной сверткой нечетких отношений.
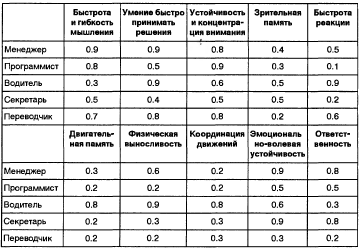
Пример: Рассмотрим ситуацию, связанную с консультированием выбора профессии. Первое нечеткое отношение Q строится на универсальных множествах X и Y, где X- множество специальностей
где
Где Y – множество психофизиологических характеристик
где
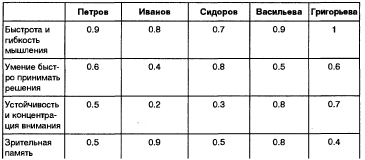
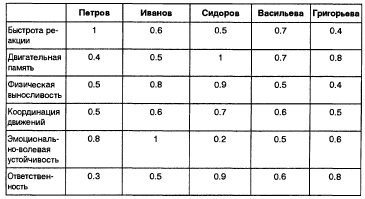
R-нечеткое отношение заданное на универсальных множествах Y и Z, где Z – множество кандидатов на обучение
где
Матрица отношений имеетследующий вид
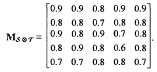
Результат операции нечеткой композиции этих отношении может быть представлен в виде матрицы результирующего нечеткого отношения:
Альтернативные операции композиции В примере показана максиминная композиция, также популярна maxprod композиция
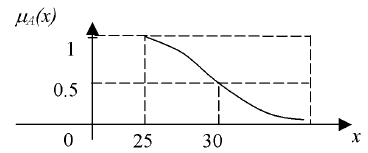
Лингвистическая переменная ЛП – это набор неч. ФП, каждая из которых имеет свое словесное обозначение. Формально ЛП определяется следующим образом (1) <β, T, X, G, M> (1) , где β - название лингвистической переменной T - терм-множество переменной или множество, содержащее наименования нечетких переменных лингвистической переменной. X - область определения или универсальное множество лингвистической переменной. G - некоторая синтаксическая процедура, позволяющая получать новые осмысленные значения лингвистической переменной, например, модификаторы «очень», «слегка», «не». M - Семантическая процедура, позволяющая поставить в соответствие каждому имени нечеткой переменной некоторую функцию принадлежности. Пример: β – скорость движения авто T – {«малая», «средняя», «высокая»} X - 0…100 км\ч G - процедура образования новых осмысленных значений с помощью модификаторов «очень», «не», «слегка», а так же логических связок «И», «ИЛИ». Например, малая или очень средняя скорость M - Процедура задания нечетких переменных
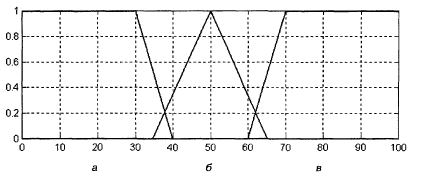
Рис.21 – Графики функций принадлежности нечетких множеств A1, A2, A3 соответствующих нечетким переменным а = «малая скорость», б = «средняя скорость», в = «высокая скорость»
|
|
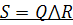 )
) (<x1 x2, …, xk>)} и
(<x1 x2, …, xk>)} и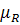 (<x1 x2, …, xk>)} называется некоторое отношение S заданное на этом же декартовом произведении универсумов, функция принадлежности которого определяется по формуле:
(<x1 x2, …, xk>)} называется некоторое отношение S заданное на этом же декартовом произведении универсумов, функция принадлежности которого определяется по формуле:
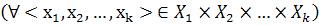
 )
)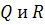 называется некоторое отношение S заданное на этом же декартовом произведении универсумов
называется некоторое отношение S заданное на этом же декартовом произведении универсумов 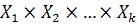 , функция принадлежности которого определяется по формуле:
, функция принадлежности которого определяется по формуле: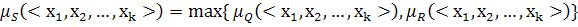
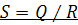 )
)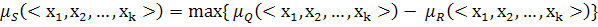
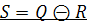 )
)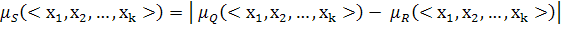
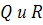 — конечные или бесконечные бинарные нечеткие отношения. Причем нечеткое отношение Q={
— конечные или бесконечные бинарные нечеткие отношения. Причем нечеткое отношение Q={ 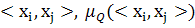 } задано на декартовом произведении универсумов
} задано на декартовом произведении универсумов 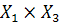 , а нечеткое отношение R={
, а нечеткое отношение R={ 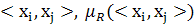 } — на декартовом произведении универсумов
} — на декартовом произведении универсумов 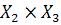
 называется нечеткое отношение, заданное на декартовом произведении
называется нечеткое отношение, заданное на декартовом произведении 
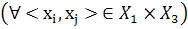
 ,
,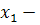 менеджер,
менеджер,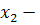 программист,
программист,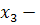 водитель,
водитель, секретарь-референт,
секретарь-референт,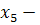 переводчик
переводчик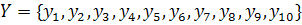 ,
,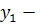 быстрота и гибкость мышления,
быстрота и гибкость мышления,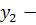 умение быстро принимать решения,
умение быстро принимать решения, устойчивость и концентрация внимания,
устойчивость и концентрация внимания,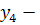 зрительная память,
зрительная память,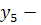 быстрота реакции,
быстрота реакции,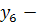 двигательная память,
двигательная память,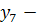 физическая выносливость,
физическая выносливость,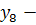 координация движений,
координация движений, эмоционально-волевая устойчивость,
эмоционально-волевая устойчивость,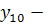 ответственность
ответственность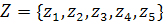 ,
, Петров,
Петров, Иванов,
Иванов,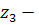 Сидоров,
Сидоров, Васильева,
Васильева,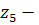 Григорьева
Григорьева