|
|
II. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОКЭлектрический ток, его характеристики и условия существования Электрическим током называется упорядоченное движение заряженных частиц. Условия появления и существования тока: 1) Наличие свободных электрических зарядов. В металлах – свободных электронов, в электролитах – положительных и отрицательных ионов, в плазме – свободных электронов и ионов, в полупроводниках – электронов проводимости и дырок. 2) Наличие внешнего электрического поля. Ток возникает под действием электрического поля. При этом равновесное распределение зарядов в проводнике нарушается, а его поверхность и объем перестают быть эквипотенциальными. На поверхности проводника действует тангенциальная напряженность Еτ ≠ 0 и Евнутри ≠ 0. Электрический ток продолжается до тех пор, пока все точки проводника не станут эквипотенциальными. Таким образом, для поддержания тока необходим источник электрической энергии – устройство, в котором осуществляется преобразование какого-либо вида энергии в энергию электрического тока. Количественной мерой электрического тока является сила тока Электрический ток называется постоянным, если его направление и сила не изменяются с течением времени: Направление тока определяется вектором плотности тока j. За направление тока условно принимают направление движения положительных зарядов.
где α – угол между векторами n и j ; dS = n dS. di = dNj – поток вектора j через площадку dS. Тогда сила тока через произвольную поверхность S будет: Для постоянного тока в однородном проводнике с поперечным сечением S: I = jS . Плотность тока в металле
где n – концентрация электронов проводимости, -е – заряд электрона; ‹V› – средняя скорость дрейфа электронов.
Закон Ома в дифференциальной форме с точки зрения классической Теории проводимости металлов (КТПМ)
Создатели классической электронной теории проводимости – Друдэ и Лоренц. Согласно этой теории высокая электропроводность металлов объясняется: 1) наличием громадного количества свободных электронов; 2) движение электронов подчиняется законам классической механики Ньютона; 3) в этой теории пренебрегают взаимодействием электронов между собой, а взаимодействие электронов с положительными ионами сводят только к соударениям. Таким образом, электроны проводимости в теории Друдэ-Лоренца рассматриваются как электронный газ, обладающий свойствами одноатомного идеального газа. j = ne‹V›.(2.1) На каждый электрон действует сила F = eE, которая сообщает ему ускорение:
Скорость электрона изменяется от 0 до Vmax. Тогда средняя скорость дрейфа электрона:
После подстановки в формулу (2.1), получим
1/γ = ρ – удельное сопротивление проводника. Таким образом, получаем
закон Ома в дифференциальной форме:плотность тока проводимости j равна произведению удельной электропроводности проводника на напряженность электрического поля в проводнике. Вектора j и Е имеют одинаковое направление.
Обобщенный закон Ома
Если в проводнике создать электрическое поле и не принять мер для его поддержания, то перемещение носителей тока приведет очень быстро к тому, что напряженность внутри проводника станет равной нулю и ток прекратится. Таким образом, при наличии лишь кулоновских сил невозможно поддерживать в цепи электрический ток. Следовательно, для поддержания в цепи постоянного тока необходимо, чтобы на носители тока действовали помимо кулоновских сил иные силы, не электростатического происхождения, называемые сторонними. Если кулоновские силы вызывают соединение разноименных зарядов, выравнивание потенциала и исчезновение поля в проводнике, то сторонние силы, наоборот вызывают разделение разноименных зарядов и поддерживают разность потенциалов на концах проводника. Сторонние силы действуют на носители тока внутри источников электрической энергии (гальванических элементов, аккумуляторов, электрических генераторов и т.п.). В общем случае, на носитель тока q, действует сила:
где
Умножим скалярно обе части равенства на dl.|dl | – длина элемента проводника. Вектор dlнаправлен по току.
Учитывая Интегрируем данное выражение по длине участка цепи 1-2:
электродвижущая сила (ЭДС), действующая на участке 1-2.
Напряжение – это физическая величина, численно равная суммарной работе, совершаемой кулоновскими и сторонними силами при перемещении по участку 1-2 единичного положительного заряда. Таким образом, U12 = (φ1 – φ2) + Е12. Сопротивление на участке 1-2:
Закон Джоуля-Ленца
При столкновении электронов (носителей тока) с атомами электроны теряют свою энергию. Эта энергия переходит в энергию хаотического движения атомов, т.е. в тепловую. Q = I 2R t – закон Джоуля-Ленца для постоянного тока I = const. Если ток изменяется со временем, то Данные формулы – интегральная форма записи закона, она выражает тепло, выделяющееся во всем проводнике. Дифференциальная форма записи закона Джоуля-Ленца позволяет вычислить тепло, выделяющееся в различных точках проводника: Qуд = ρ j 2, где ρ – удельное сопротивление, j – плотность тока, |
|
 – скалярная физическая величина, равная заряду dq переносимого сквозь поверхность S за малый промежуток времени dt (в единицу времени). Под S понимают поперечное сечение проводника.
– скалярная физическая величина, равная заряду dq переносимого сквозь поверхность S за малый промежуток времени dt (в единицу времени). Под S понимают поперечное сечение проводника. .
. – плотность тока численно равна отношению силы тока di сквозь малый элемент поверхности, перпендикулярный направлению тока, к величине этого элемента поверхности.
– плотность тока численно равна отношению силы тока di сквозь малый элемент поверхности, перпендикулярный направлению тока, к величине этого элемента поверхности.
 ,
, – поток вектора j через поверхность S.
– поток вектора j через поверхность S. ,
, ,
,  .
. – среднее время свободного пробега электрона (т.е. среднее время между двумя последовательными соударениями).
– среднее время свободного пробега электрона (т.е. среднее время между двумя последовательными соударениями).

 .
. , т.е. j ~ E;
, т.е. j ~ E;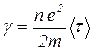 - удельная электропроводность;
- удельная электропроводность; –
–
 – напряженность поля кулоновских сил,
– напряженность поля кулоновских сил,  – напряженность поля сторонних сил. Тогда
– напряженность поля сторонних сил. Тогда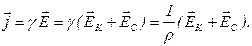
 или
или 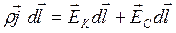
 , получим
, получим 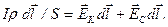
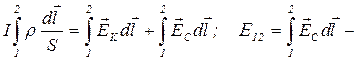
 – ЭДС численно равна работе, совершаемой сторонними силами при перемещении единичного положительного заряда.
– ЭДС численно равна работе, совершаемой сторонними силами при перемещении единичного положительного заряда. – напряжение на участке цепи 1-2.
– напряжение на участке цепи 1-2. . Если r=const, S=const, то
. Если r=const, S=const, то  ,
, - обобщенный закон Ома или
- обобщенный закон Ома или  .
.


 .
.



 .
.
 3.
3.
 .
.
 .
. – количество тепла, выделяющееся в единицу времени в единице объема.
– количество тепла, выделяющееся в единицу времени в единице объема.