|
|
Краткие теоретические сведения
В жидкостях и газах при перемещении одних слоев относительно других возникают силы внутреннего трения, или вязкости, которые определяются законом Ньютона:
где
Механизм внутреннего трения в жидкостях и газах неодинаков, так как в них различен характер теплового движения молекул. Вязкость жидкости обусловлена молекулярным взаимодействием, ограничивающим движение молекул. Каждая молекула жидкости находится в потенциальной ямы, создаваемой соседними молекулами. Поэтому молекулы жидкости совершают колебательное движения около положения равновесия, то есть внутри потенциальной ямы. Глубина потенциальной ямы незначительно превышает среднюю кинетическую энергию, поэтому, получив дополнительную энергию при столкновении с другими молекулами, она может перескочить в новое положение равновесия. Энергия, которую должна получить молекула, чтобы из одного положения перейти в другой называется энергия активации W, а время нахождения молекулы в положении равновесия – временем “оседлой жизни” t. Перескок молекул между соседними положениями равновесия является случайным процессом. Вероятность того, что такой перескок произойдет за время одного периода t0, в соответствии с законом Больцмана, составляет:
Обратная величина
где k – постоянная Больцмана; Коэффициент динамической вязкости зависит от
где А – константа, определяемая свойствами жидкости. Формула (4) является приближенной, но она достаточно хорошо описывает вязкость многих жидкостей в том числе и глицерина в интервале температур, задаваемом в данной работе. Строгая теория вязкости носит квантовый характер и является очень сложной. Из формулы (4) видно, что с уменьшением температуры вязкость жидкости возрастает. В ряде случаев она становится настолько большой, что жидкость затвердевает без образования кристаллической решетки. В этом заключается механизм образования аморфных твердых тел. При малых скоростях движения тела в жидкости слой жидкости, непосредственно прилегающий к телу, прилипает к нему и движется со скоростью тела. По мере удаления от поверхности тела скорость слоев жидкости будет уменьшаться, но они будут двигаться параллельно. Такое слоистое движение жидкости называется ламинарным. При больших скоростях движения жидкости становится неустойчивым и называется турбулентным, при котором частицы жидкости движутся по сложным траекториям со скоростями, изменяющимися беспорядочным образом. В результате происходит перемешивание жидкости и образуются вихри. Характер движения жидкости определяются безразмерной величиной Re, называемой числом Рейнольдса. Re зависит от формы тела и свойств жидкости. При движении шарика радиусом R со скоростью
При малых Re (<10) движение жидкости будет ламинарным. В этом случае на тело будет действовать сила сопротивления, пропорциональная скорости:
где r – коэффициент сопротивления. Для тела сферической формы
Сила сопротивления шарика примет вид:
Формула (7) называется законом Стокса. При падении шарика в жидкости на него действуют силы: сопротивления
Решение уравнения (8) описывает характер движения шарика на всех участках падения. Прежде чем привести это решение, проанализируем его качественно. Примем при t = 0 скорость
где В начале движения скорость
Из уравнения (10) видно, что на начальном этапе шарик движется с ускорением:
Согласно уравнению (8), по мере увеличения скорости возрастает сила сопротивления и ускорение уменьшается. При большом времени движения (t®¥) сила сопротивления уравновешивается равнодействующей сил
Из приведенных рассуждений ясно, что скорость будет возрастать с увеличением времени движения и при t®¥,
График зависимости (12) представлен на рис. 2 (кривая линия б).
Чем больше будет ускорение а0, т.е. круче касательная к кривой
Итак, после прохождения шариком расстояния
Сила тяжести
где r - плотность вещества шарика. Выталкивающая сила определяется по закону Архимеда:
Подставив (15), (16) и (7) в уравнение (14), получим
Отсюда найдем
Измерив
Описание установки
Схематично установка изображена на рис. 3.
Порядок выполнения работы Задание 1. Определить коэффициент динамической вязкости глицерина при комнатной температуре. 1. Измерить штангенциркулем диаметр шарика в различных местах. 2. Опустить шарик по центру цилиндра с глицерином. При прохождении им верхний метки на цилиндре включить секундомер и выключить его при прохождении шариком нижней метки. Такие измерения выполнить с пятью различными шариками. Данные занести в табл. 1. Таблица 1.
3. По результатам каждого измерения вычислить значение коэффициента динамической вязкости по формуле (18), полученной из (17) путем замены R на D/2,
4. Вычислить среднее значение вязкости <h>, абсолютную ошибку Dh, относительную погрешность измерения вязкости e. 5. Записать конечный результат в виде h = (<h>±Dh). Задание 2. Определить температурную зависимость коэффициента динамической вязкости глицерина и вычислить энергию активации. 1. Измерить штангенциркулем диаметр D всех шариков, выданных преподавателем. 2. С разрешения преподавателя включить нагреватель термостата кнопкой К1 и насос кнопкой К2. 3. При различных температурах измерить время падения шарика. При каждой температуре опыт проводится один раз. Интервал температур и количество опытов задается преподавателем. (Ориентировочные данные - проводить измерения через 5°С от комнатной температуры до 50°С). 4. Вычислить коэффициент динамической вязкости при различных температурах по формуле (18). 5. Заполнить табл. 2, построить график зависимости h = f(t°С). Таблица 2.
Прологарифмировав выражение (4):
6. Построить график зависимости (19) в координатах 7. Вычислить угловой коэффициент прямой (19) по формуле:
где 8. Найти энергию активации молекул глицерина по формуле:
Контрольные вопросы
1. Напишите закон Ньютона для силы внутреннего трения и поясните все величины, входящие в него. 2. В каких единицах измеряется коэффициент динамической вязкости, и какую размерность он имеет? 3. Как изменяется h с изменением температуры в газах и жидкостях? Чем объясняется различный характер этих зависимостей? 4. При каких условиях движение жидкости будет ламинарным? 5. Применив метод размерности, выведите формулу Стокса (при затруднении вывода см. [3] или [5]). 6. Опишите характер движения шарика в глицерине. 7. Какую величину называют временем релаксации? Как она изменится для шарика: а) при увеличении вязкости жидкости? б) при увеличении размера шарика? 8. Запишите уравнение движения шарика в глицерине. 9. Как определить положение верхней метки на цилиндре? От каких величин она зависит? 10. Как изменится характер движения шарика, если до вхождения в глицерин он будет иметь скорость, отличную от нуля? Изобразите для этого случая зависимость 11. Выведете расчетную формулу для h, для W. Библиографический список
1. Курс физики: Учебник для вузов: в 2-х т. Т. 1 / Под ред. В. Н. Лозовского. – СПб.: Лань, 2006. – Гл. 5.1 § 5.6–5.7. 2. Детлаф, А. А. Курс физики / А. А. Детлаф, Б. М. Яворский. – М.: Высш. шк., 1999. – § 10.7–10. 3.Трофимова, Т. И. Курс физики / Трофимова Т.И. – М.: Академия, 2004. – § 31–32. 4. Савельев, И. В. Курс общей физики в 3-х т. Т.1 / И. В. Савельев.– СПб.: Лань, 2005. – §75–76. 5. Гольдин, Л. Л. Лабораторные занятия по физике. / Л. Л. Гольдин.– М.: Наука, 1983. – § 3.15.
ЛАБОРАТОРНАЯ РАБОТА № 21 ИЗМЕРЕНИЕ ТЕПЛОПРОВОДНОСТИ ГАЗА Цель работы: определить коэффициент теплопроводности воздуха при различных температурах. Оборудование: цилиндр с нитью-проволокой, выпрямитель, амперметр, вольтметр, реостат.
|
|
 (1)
(1) - коэффициент внутреннего трения, или коэффициент динамической вязкости, или просто вязкость;
- коэффициент внутреннего трения, или коэффициент динамической вязкости, или просто вязкость;  – модуль градиента скорости, который показывает, как быстро изменяется величина скорости в направлении внутренней нормали к поверхности слоя; DS – поверхность соприкасающихся слоёв (рис. 1).
– модуль градиента скорости, который показывает, как быстро изменяется величина скорости в направлении внутренней нормали к поверхности слоя; DS – поверхность соприкасающихся слоёв (рис. 1). Уравнение (1) является определяющим для установления единиц измерений коэффициента динамической вязкости. Размерность вязкости ML-1×T-1. В СИ h измеряется в Па×с=кг/(м×с), а в СГС в пуазах. П (пуаз) = г/(cм×с).
Уравнение (1) является определяющим для установления единиц измерений коэффициента динамической вязкости. Размерность вязкости ML-1×T-1. В СИ h измеряется в Па×с=кг/(м×с), а в СГС в пуазах. П (пуаз) = г/(cм×с).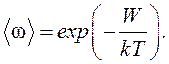 (2)
(2) определяет среднее число колебаний, которое должна совершить молекула, чтобы покинуть положение равновесия. Среднее время “оседлой жизни” молекулы:
определяет среднее число колебаний, которое должна совершить молекула, чтобы покинуть положение равновесия. Среднее время “оседлой жизни” молекулы: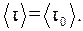
 , (3)
, (3) - средний период колебаний молекулы около положения равновесия.
- средний период колебаний молекулы около положения равновесия. , чем реже молекулы меняют положение равновесия, тем больше вязкость. Используя модель скачков молекул, Я.И. Френкель показал, что вязкость изменяется по экспоненциальному закону:
, чем реже молекулы меняют положение равновесия, тем больше вязкость. Используя модель скачков молекул, Я.И. Френкель показал, что вязкость изменяется по экспоненциальному закону: (4)
(4) в жидкости с плотностью rж:
в жидкости с плотностью rж: (5)
(5) , (6)
, (6)
 (7)
(7) , тяжести
, тяжести  , выталкивающая
, выталкивающая  . Запишем уравнение движения в проекциях на направление движения:
. Запишем уравнение движения в проекциях на направление движения: . (8)
. (8) . Перепишем уравнение (8) в видe:
. Перепишем уравнение (8) в видe: , (9)
, (9) - характерная величина, имеющая размерность времени и называется временем релаксации.
- характерная величина, имеющая размерность времени и называется временем релаксации.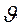 мала, слагаемым
мала, слагаемым  в уравнении (9) можно пренебречь и оно примет вид:
в уравнении (9) можно пренебречь и оно примет вид: . (10)
. (10)
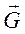 и
и  , и шарик будет двигаться равномерно с установившейся скоростью
, и шарик будет двигаться равномерно с установившейся скоростью  . Так как при равномерном движении
. Так как при равномерном движении  , то из уравнения (9) находим:
, то из уравнения (9) находим: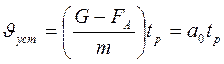 . (11)
. (11) , т.е. эта зависимость будет экспоненциальной. Строгую зависимость
, т.е. эта зависимость будет экспоненциальной. Строгую зависимость 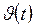 дает решение дифференциального уравнения (9). Опуская математическую часть задачи, приведем окончательный результат:
дает решение дифференциального уравнения (9). Опуская математическую часть задачи, приведем окончательный результат: (12)
(12) Проведем касательную к начальному участку кривой (см. рис. 2). Так как угловой коэффициент этой прямой числено равен а0, то уравнение этой линии будет
Проведем касательную к начальному участку кривой (см. рис. 2). Так как угловой коэффициент этой прямой числено равен а0, то уравнение этой линии будет  и согласно (11) она пересечет
и согласно (11) она пересечет  , тем меньше tр. Следовательно, время релаксации характеризует быстроту приближения к установившемуся значению скорости, поэтому его также называют временем переходного процесса. На практике принимается, что переходные процессы вида (12) заканчиваются за время ~ 3tр. За это время тело пройдет расстояние:
, тем меньше tр. Следовательно, время релаксации характеризует быстроту приближения к установившемуся значению скорости, поэтому его также называют временем переходного процесса. На практике принимается, что переходные процессы вида (12) заканчиваются за время ~ 3tр. За это время тело пройдет расстояние:
 его движение можно считать равномерным. Уравнение движения (24) в этом случае примет вид:
его движение можно считать равномерным. Уравнение движения (24) в этом случае примет вид: . (14)
. (14) , (15)
, (15)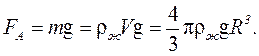 (16)
(16) .
. . (17)
. (17)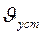 и R, взяв табличные значения плотности вещества шарика и глицерина, можно определить вязкость глицерина по формуле (17).
и R, взяв табличные значения плотности вещества шарика и глицерина, можно определить вязкость глицерина по формуле (17). В термостате вода нагревается и по резиновым шлангам насосом, установленным внутри термостата, прокачивается через полость между внутренними и внешними стенками цилиндра. В результате нагревается глицерин в цилиндре. Температура воды определяется по термометру. Считается, что температура глицерина такая же, как у воды.
В термостате вода нагревается и по резиновым шлангам насосом, установленным внутри термостата, прокачивается через полость между внутренними и внешними стенками цилиндра. В результате нагревается глицерин в цилиндре. Температура воды определяется по термометру. Считается, что температура глицерина такая же, как у воды. на h/t (h – расстояние между метками на цилиндре):
на h/t (h – расстояние между метками на цилиндре): . (18)
. (18) (19)
(19) , (1/T)103.
, (1/T)103.
 и
и  - произвольные значения точек на оси абсцисс, разделенных на 103, а
- произвольные значения точек на оси абсцисс, разделенных на 103, а  и
и 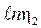 – соответствующие значения на оси ординат.
– соответствующие значения на оси ординат.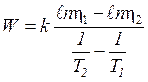 .
. .
.