|
|
Основні закономірності термодинаміки необоротних процесів
Розглянемо найбільш загальні формулювання аксіом термодинаміки необхідних процесів, що належать Онзагеру. Метод Онзагера базується на ряді аналогій з механікою. З механіки відомо, що швидкість стаціонарного руху тіла (потоку) пропорційна діючій на нього силі. Це положення Онзагер розповсюдив і на всі стаціонарні необоротні термодинамічні процеси. Перший постулат Онзагера дозволяє описати потоки. Вважається, що будь-який потік речовини, тепла, струму (І) пропорційний діючій у системі термодинамічній силі (х). Припущення про лінійний характер зв'язків у термодинамічних рівняннях, що зв'язують потік і силу, яка його викликає, є першим положенням теорії Онзагера. У найпростішому випадку для одного потоку і однієї сили, що його викликає,
де L – деякий феноменологічний фактор Онзагера. Якщо в системі є "і" потоків і "к" сил, що їх викликають, то, враховуючи взаємодію потоків між собою, в загальному випадку одержимо рівняння
Вважається, що і–тий потік залежить від всіх термодинамічних сил, що діють в системі. Це – друге положення теорії Онзагера. Діагональні коефіцієнти Li,к при і = к показують вплив сили на свій потік (наприклад, теплової сили на тепловий потік), а при і ¹ к показують вплив даної сили на чужий потік (наприклад, теплової сили на дифузію). Третє положення теорії Онзагера випливає з припущення, що дія сили на чужі потоки симетрична. Наприклад, теплова сила діє на дифузійний потік таким же чином, як дифузійна сила на тепловий потік, тобто
Останнє положення відоме як співвідношення взаємності Онзагера і має важливу роль в термодинаміці необоротних процесів. Важливим в термодинаміці необоротних процесів є висвітлення того, що слід розуміти в кожному випадку під термодинамічною силою. Для вирішення цього питання знов використовують аналогію з механікою. З механіки відомо, що швидкість зміни енергії (Е) в системі дорівнює добутку швидкості потоку (І) на силу (х), тобто
Як термодинамічний аналог величини
і далі, поділивши на Dt, одержимо:
або
Багато які металургійні процеси проходять з передачею теплоти. Як приклад, знайдемо швидкість зміни ентропії при передачі теплоти від одного резервуара до іншого через перегородку (рис. 7.1). Ентропія буде збільшуватись за рахунок передачі теплоти від резервуара з температурою Т2 до резервуара з температурою Т1. Припустимо, що від резервуара з температурою Т2 відібрано Q теплоти і ця теплота передана через перегородку в резервуар з температурою Т1. При цьому ентропія першого резервуара зміниться на Загальна зміна ентропії при переході такої кількості теплоти через перегородку дорівнює сумі: DS = DS1 + DS2, тобто
З рівняння (7.4) знаходимо швидкість зміни ентропії
Додатний потік (w) теплоти в напрямку зменшення температури однаковий на обох кінцях перегородки. При стаціонарному процесі передача теплоти вздовж перегородки речовини певного складу
У випадку стаціонарного процесу при невеликій різниці температур DТ(DТ<<Т1)
звідки швидкість зміни ентропії в одиниці об'єму перегородки (V = sDх, де s – площа перегородки; Dх – її товщина)
але де І – тепловий потік через перегородку на осі х, тобто кількість теплоти, що проходить через одиницю перерізу перегородки за одиницю часу. Підставивши ці значення в рівняння (7.7), одержимо
або Зіставляючи рівняння (7.4) і (7.12), знаходимо, що теплова сила
Онзагер узагальнив цей висновок і показав, що для будь-якого потоку
де Іі – потоки і хі – сили, що їх викликають. Аналогічно можна одержати вирази для інших термодинамічних сил. Наприклад, для дифузійного потоку:
де m – маса дифундуючої речовини (термодинамічна сила);
де m - хімічний потенціал дифундуючої речовини. Якщо дифузія протікає в ізотермічних умовах, то Подібним чином підходять до розгляду будь-яких стаціонарних необоротних металургійних процесів.
|
|
 , (7.1)
, (7.1)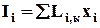 . (7.2)
. (7.2)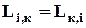 . (7.3)
. (7.3) .
.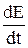 можна прийняти зміну ентропії (DS) за одиницю часу в одиниці об'єму (V):
можна прийняти зміну ентропії (DS) за одиницю часу в одиниці об'єму (V):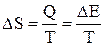 ,
,
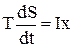 . (7.4)
. (7.4)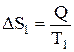 , а другого – на
, а другого – на  .
. . (7.5)
. (7.5)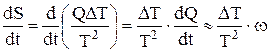 . (7.6)
. (7.6) є сталою величиною. При підрахунку координати х вздовж перегородки від гарячого кінця величина градієнта є від'ємною
є сталою величиною. При підрахунку координати х вздовж перегородки від гарячого кінця величина градієнта є від'ємною 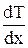 <0. Враховуючи це, температуру між гарячим кінцем перегородки (Т2; х=0) і холодним кінцем або будь-яким перерізом з координатою (х) і температурою (Т1) можна представити таким чином
<0. Враховуючи це, температуру між гарячим кінцем перегородки (Т2; х=0) і холодним кінцем або будь-яким перерізом з координатою (х) і температурою (Т1) можна представити таким чином . (7.7)
. (7.7)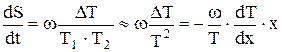 , (7.8)
, (7.8)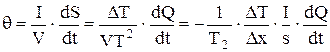 , (7.9)
, (7.9) і
і 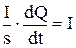 , (7.10)
, (7.10) (7.11)
(7.11)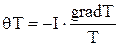 . (7.12)
. (7.12)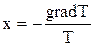 . (7.13)
. (7.13) ,
,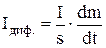 ,
, ,
, .
.