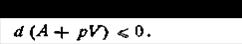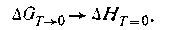Термодинамические потенциалы. Характеристические функции

Как показано ранее, в изолированных системах энтропия мо­жет только увеличиваться и достигать своего максимума, когда система находится в равновесии. Поэтому она и используется для суждения о направлении самопроизвольных процессов в таких системах. Однако в естественных условиях подавляющее боль­шинство процессов протекает в неизолированных системах. По этой причине для них потребовалось ввести другие критерии рав­новесия. Направление процессов при этом можно характеризо­вать работой, которую они могут совершать при определенных условиях.

Величина работы, как известно, зависит от пути процесса. Поэтому, казалось бы, она не может служить критерием для суждения о направленности того или иного процесса. Однако если ограничиться рассмотрением частного случая процесса при посто­янной температуре, то оказывается, что максимальная работа при обратимом его протекании будет определяться изменением некоторой функции состояния. Действительно, мо­жем написать δW ≤ TdS — dU, или при Т = const

1.62

Как видим, при обратимом изотермическом процессе работа, про­изводимая системой, равна убыли некоторой функции состояния

Функция (U — TS) получила название изохорно-изотермического потенциала (сокращенно изохорный потенциал) или свободной энергии. Иногда эту функцию называют еще потенциалом Гельмгольца.

При этом для всякого изотермического процесса

1.64

Таким образом, максимальная работа при изохорно-изотермических равновесных процессах равна убыли свободной энергии си­стемы, т. е. W = —∆А, или в общем случае

1.65

Изменение свободной энергии определяется только начальным и конечным состоянием системы и не зависит от характера процесса. Величина работы может зависеть лишь от способа проведения процесса. Так, например, при необратимом процессе произведен­ная работа всегда будет меньше убыли свободной энергии, так как при этом часть изменения свободной энергии неизбежно превра­щается в теплоту.

Из определения А следует, что U = А + TS, т. е. что внутренняя энергия системы состоит из двух частей: свободной энергии при постоянном объеме и связанной энергии TS. Как видим, свя­занная энергия равна произведению энтропии на абсолютную тем­пературу. Свободная энергия — это та часть внутренней энергии, которая при обратимом изотермическом процессе может быть пол­ностью превращена в работу.

Если к условию постоянства температуры добавить условие постоянства объема, т. е. δW = pdV = 0, то

1.66

Следовательно, при постоянных температуре и объеме свободная энергия не изменяется при обратимых процессах, а при необрати­мых может только убывать. Это означает, что данная функция дей­ствительно является критерием, который позволяет судить о на­правлении процессов в незамкнутых системах. Очевидно, для таких систем условием равновесия является минимум свободной энергии (при постоянных V и Т).

Как видим, условия, которым должны удовлетворять процессы для того, чтобы по изменениям величины А можно было судить о направлении этих процессов, иные, чем для энтропии. Для энтропии это было условие постоянства внутренней энергии и объема (изо­лированная система), для изохорно-изотермического потенциала это условие постоянства объема и температуры — легко измеряемых параметров системы. Величина А, являясь производным понятием по отношению к энтропии, представляет собой практически более удобный критерий для характеристики направленности процессов, чем энтропия.

Таким образом, свободная энергия при постоянных V и Т в естественных (самопроизвольных) процессах стремится умень­шиться. Когда она достигает минимального значения (совмести­мого с данными V и Т), система приходит в равновесие.

В технике большинство процессов совершается не при посто­янном объеме, а при постоянном давлении. Поэтому кроме сво­бодной энергии при постоянном объеме целесообразно ввести та­кую функцию состояния, которая служила бы критерием равнове­сия в условиях постоянства давления и температуры.

Если объем системы изменяется, то pdV ≤ – dA или dA + pdV ≤ 0. При постоянном давлении

1.67

Таким образом, новая функция состояния, называемая изобарно-изотермическим потенциалом (или потенциалом Гиббса), обоз­начается обычно через G и определяется уравнениями:

1.68

т. е. G находится в таком же отношении к функции А, как энталь­пия Н к внутренней энергии U.

Для любого процесса ∆G = ∆A + ∆(рV). Отсюда следует, что для любого изобарного процесса

1.69

Для всякого изотермического процесса

1.70

Согласно уравнениям (I.68) и (I.70) можно вывести урав­нение

1.71

где W_м— максимальная полезная работа, равная максимальной работе W за вычетом работы против внешнего давления. Для изо­термического процесса при р = const

1.72

При обратимых процессах величина G не изменяется, а при необратимых может только убывать. Следовательно, равновесное состояние системы при постоянных давлении и температуре соот­ветствует минимуму изобарно-изотермического потенциала.

Суммируя все выше изложенное, можно сделать вывод о том, что описание термодинамических свойств любой системы может быть выражено через термодинамические функции системы: U = f(S, V), Н = f(S, р), А = f(V, T), G = =f(p, T).

Третье начало термодинамики

Третье начало термодинамики, или тепловая теорема, было сформулировано Нернстом в 1906 г. и потому часто называется его именем. Большое значение в развитии этой теоремы имели работы М. Планка (1911). Тепловая теорема Нернста имеет следующую формулировку: при абсолютном нуле энтропия любого однород­ного тела равна нулю.

При этом делается допущение, что при T→0 зависимость теп­лового эффекта и максимальной работы для конденсированных систем выражается равенством

1.73

Из уравнения (1.73) следует, что W = 0.

Согласно третьему закону термодинамики уравнение (I.73) при T→0 принимает вид

Таким образом, изменение изобарно-изотермического потенциала реакции становится равным изменению энтальпии. Расхождение между этими функциями состояния увеличивается с повышением температуры. Другими словами, с повышением температуры на­правление химической реакции зависит уже от двух факторов — от знака изменения энтальпии и от значения изменения энтропии.

В 1907 г. Эйнштейн доказал, что теплоемкость твердых тел при абсолютном нуле (Т=0) должна быть равна нулю. Благодаря тепловой теореме Нернста оказалось возможным определять абсолютную величину энтропии на основании измерения теплоемкостей при разных температурах. На основании этой теоремы можно вывести известные соотношения, которые позволяют по тепловому эффекту реакции вычислять ее свободную энергию, а зная последнюю, можно предсказать и направление реакции.

Вопросы для самоподготовки

1. Дайте определение основных термодинамических понятий (система, фаза, компонент и др.).

2. Назовите основные термодинамические процессы и функции их определяющие.

3. Сформулируйте 1-ый и 2-ой законы термодинамики. Запишите их математические выражения.

4. Закон Гесса – основной закон термохимии. Опишите методы определения тепловых эффектов реакции.

5. Дайте понятие энтропии, свободной энергии и максимальной работы. Как изменяется энтропия в процессе жизнедеятельности и гибели биологической системы.

6. Сформулируйте третье начало термодинамики и дайте понятие химического потенциала.

ЗАДАНИЯ К ЛАБОРАТОРНОЙ РАБОТЕ 1

ЗАДАНИЕ 1. Определение теплового эффекта растворения солей.

Цель работы:

1. Освоить методику калориметрического метода определения тепловых эффектов реакции (см. с.76-78).

2. Определить тепловой эффект (изменение энтальпии) растворения заданной соли [ Cо(NH₂)₂, KBr, NaNO₃, …].

3. Рассчитать относительную ошибку и сделать выводы.

ЗАДАНИЕ 2. Определение теплот гидратации солей.

Цель работы:

1. Освоить методику калориметрического метода определения тепловых эффектов реакции (см. с.76-78).

2. Определить тепловые эффекты солей СиSO₄ и СиSO₄×5Н₂О; Na₂НРО₄ и Na₂НРО₄×2Н₂О и др.

3. Рассчитать теплоту гидратации соли (см. ур-ние 1.74).

ЗАДАНИЕ 3. Определение теплоты взаимодействия почвы с водой.

Цель работы:

1. Освоить калориметрический метод определения тепловых эффектов (см. с.76-78).

2. Определить теплоту взаимодействия различных почв (чернозем, бурая лесная и др.) с водой.

3. Сопоставить данные о теплотах взаимодействия почв с водой.