|
|
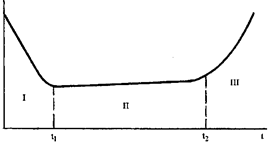
Этапы функционирования изделия. Экспоненциальный закон и закон Вейбулла распределения вероятности отказа изделийПричина возникновения внезапных отказов не связана с изменением состояния изделия и временем его предыдущей работы, а зависит от неблагоприятного сочетания множества факторов. При возникновении внезапных отказов величина интенсивности отказов l (показатель безотказности) практически не зависит от времени. Возникновение постепенных отказов определяется процессом постепенного накопления повреждений в изделии. На практике установлено, что изменение интенсивности отказов в течение всего жизненного цикла изделия можно представить обобщенной зависимостью в виде рисунка 5. На этой зависимости можно выделить три различных участка. На первом участке, называемом периодом приработки, интенсивность отказов в зависимости от времени эксплуатации уменьшается. В этот период выявляются и устраняются случайные отказы, вызванные явными ошибками производства (неправильная регулировка, неточная сборка и т.д.), отказы, связанные с отклонениями фактических условий работы и нагрузок от предполагаемых при выполнении проектных работ, а также отказы, связанные с приработкой различных узлов и сопряжений. Период приработки обычно включают в продолжительность обкаточных или приработочных испытаний.
Рисунок 5 - Зависимость интенсивности отказа изделия от времени его эксплуатации На втором участке интенсивность отказов для технического изделия остается примерно постоянной. Этот период получил название периода нормальной эксплуатации. В этот период постепенные (износные) отказы еще не проявляются, а могут возникать только внезапные отказы. Третий период получил название периода естественного старения материалов. В этот период кроме случайных отказов начинают возникать постепенные отказы, вызванные накоплением износных, коррозионных, усталостных, деструкционных и других повреждений. Вероятность возникновения отказа изделия с течением времени возрастает, поэтому эксплуатация изделия становится небезопасной или нерентабельной и поэтому она должна быть прекращена. Изделие направляется в ремонт или списывается. Установим зависимость вероятности безотказной работы от времени, используя в качестве основного параметра интенсивность отказов. С этой целью используем соотношение (14) для интенсивности отказов, из которого получим дифференциальное уравнение и проведя интегрирование в пределах от 0 до t с учетом того факта, что РH(0)= 1, будем иметь:
Соотношение (16) получило название основного уравнения теории надежности. Для периода нормальной эксплуатации l=const. Подставляя это значение в (16), получим экспоненциальный закон теории надежности:
Распределение (17) является однопараметрическим, так как зависит от одного параметра l, который выражается через математическое ожидание и дисперсию на основе следующих соотношений: Из соотношения (17) легко получить, что при наработке t=mT вероятность безотказной работы очень мала Pн(mT)=0,368 и даже при наработке t в десять раз меньше, чем средняя наработка до отказа mT, вероятность безотказной работы составляет 0,905, что с точки зрения надежности является часто недостаточной величиной. Поэтому для обеспечения высокой надежности изделия, подчиняющегося экспоненциальному закону необходимо назначать ресурсы много меньше, чем средняя наработка до отказа. В связи с простотой аналитического выражения экспоненциальное распределение нашло очень широкое применение в теории надежности. Его применяют: 1) для всех систем в период нормального функционирования при возникновении только внезапных отказов; 2) для всех систем при рассмотрении небольших отрезков времени, на которых можно считать l@const; 3) сложных систем, состоящих из большого числа элементов. На первом и третьем участке (рис. 5) интенсивность отказов зависит от времени и для аппроксимации этой зависимости используется степенная функция в виде:
где параметр Подставляя (18) в (16) и выполнив интегрирование получим для функции вероятности безотказной работы, ФРВ отказов и плотности распределения соотношения:
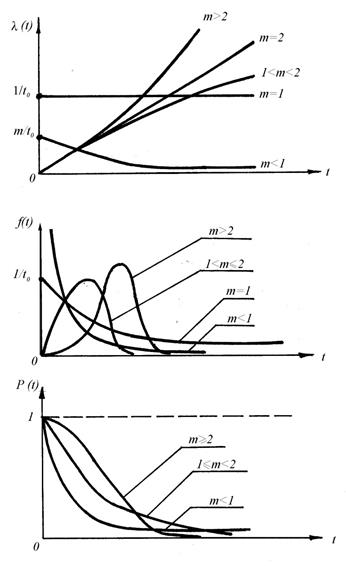
ФРВ в виде (19) получила название распределение Вейбулла. Это двухпараметрическое распределение, которое в зависимости от значения параметра формы позволяет описывать другие известные распределения (рисунок 6). Так при
Рисунок 6 - Качественный вид графиков интенсивности отказов λ(t), плотности распределения f(t) и ФРВ безотказной работы в зависимости от наработки t для различных значений параметра формы m распределения Вейбулла
Математическое ожидание и дисперсия распределения Вейбулла не выражаются через элементарные функции (табл.3). Таким образом, из обобщения известных экспериментальных данных (рис.4) без обработки большого статистического материала и построения гистограмм получен общий вид функций распределения вероятности отказов различных технических изделий. Выбор же конкретного вида ФРВ для изделия определяется экспериментальным определением параметров распределения и их статистической обработкой.
|
|
 . (16)
. (16)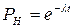 ,
,  ,
,  . (17)
. (17) .
. , (18)
, (18) >0 получил название параметра формы, а параметр
>0 получил название параметра формы, а параметр  >0 получил название параметра масштаба.
>0 получил название параметра масштаба. ,
,  ,
,  . (19)
. (19) близко к нормальному распределению.
близко к нормальному распределению.