Взаимосвязь эксплуатационных показателей с показателями качества сборочных единиц и общие требования к технологическим операциям В технологическом процессе в результате выполнения большого числа технологических операций изготавливается изделие с определенным набором эксплуатационных показателей качества  . В каждой технологической операции и в каждом технологическом переходе вследствие технологических воздействий происходит изменение формы, размеров и физико-механических свойств полуфабрикатов. Обозначим весь набор регламентированных НТД показателей на n-ой технологической операции изготовления k-ой детали через . В каждой технологической операции и в каждом технологическом переходе вследствие технологических воздействий происходит изменение формы, размеров и физико-механических свойств полуфабрикатов. Обозначим весь набор регламентированных НТД показателей на n-ой технологической операции изготовления k-ой детали через  . Для дальнейшего удобства записи математических соотношений весь набор таких показателей качества изготовления для всех операций и всех полуфабрикатов и деталей представим в виде одного упорядоченного множества . Для дальнейшего удобства записи математических соотношений весь набор таких показателей качества изготовления для всех операций и всех полуфабрикатов и деталей представим в виде одного упорядоченного множества  , где значение индекса i в определенном диапазоне соответствуют одной детали, а группа их значений в этом диапазоне соответствует определенному технологическому переходу или операции. , где значение индекса i в определенном диапазоне соответствуют одной детали, а группа их значений в этом диапазоне соответствует определенному технологическому переходу или операции.
В общем случае можно предположить, что существует некоторая функциональная зависимость, связывающая некоторый эксплуатационный показатель качества Y со всеми показателями качества  изготовления всех деталей, сборочных единиц и самого изделия на каждой технологической операции в виде: изготовления всех деталей, сборочных единиц и самого изделия на каждой технологической операции в виде:
 . (58) . (58)
В силу стохастической природы технологического процесса показатели  являются случайными величинами, которые после выполнения технологического процесса в силу контроля допусками за их рассеиванием являются центрированными случайными величинами, сгруппированными около своих математических ожиданий являются случайными величинами, которые после выполнения технологического процесса в силу контроля допусками за их рассеиванием являются центрированными случайными величинами, сгруппированными около своих математических ожиданий  с величиной стандартных отклонений с величиной стандартных отклонений  . Поэтому математическое ожидание эксплуатационного показателя качества Y в этих условиях будет определяться (п.4.5) соотношением: . Поэтому математическое ожидание эксплуатационного показателя качества Y в этих условиях будет определяться (п.4.5) соотношением:
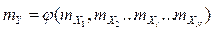 . (59) . (59)
Учитывая реализованную в технологическом процессе центрированность показателей  разложим соотношение (58) в ряд Тейлора по малым отклонениям показателей разложим соотношение (58) в ряд Тейлора по малым отклонениям показателей  от своих математических ожиданий. С точностью до первого порядка малости по таким отклонениям это разложение примет вид: от своих математических ожиданий. С точностью до первого порядка малости по таким отклонениям это разложение примет вид:
 , (60) , (60)
где производные в (60) вычисляются в точках математических ожиданий аргументов.
Используя обозначения:
 ; ;  ; ;
 ; ;  . (61) . (61)
придадим соотношению (60) нормированный вид, устанавливающий взаимосвязь между относительными отклонениями параметров от своих математических ожиданий:
 , (62) , (62)
где  . (63) . (63)
Это соотношение, связывающее между собой заведомо малые величины (  <<1 по их определению (61)), может быть получено как из физико-химических соображений (что является очень сложной задачей) или экспериментально, например, методом математического планирования эксперимента. Оно в принципе позволяет оценить относительную роль или вклад каждого показателя качества изготовления <<1 по их определению (61)), может быть получено как из физико-химических соображений (что является очень сложной задачей) или экспериментально, например, методом математического планирования эксперимента. Оно в принципе позволяет оценить относительную роль или вклад каждого показателя качества изготовления  на анализируемый эксплуатационный показатель Y. на анализируемый эксплуатационный показатель Y.
Однако, нам для проведения анализа и расчетов по соотношению аналогичному (57) необходимо найти связь коэффициентов вариации  с коэффициентом вариации с коэффициентом вариации 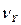 . Для этого можно воспользоваться соотношением (31), сделав предположение о нормальном законе распределения всех случайных величин, входящих в (62) или применить операцию вычисления дисперсии (9) к левой и правой частей соотношения (62). . Для этого можно воспользоваться соотношением (31), сделав предположение о нормальном законе распределения всех случайных величин, входящих в (62) или применить операцию вычисления дисперсии (9) к левой и правой частей соотношения (62).
Применяя операцию вычисления дисперсии, используя линейность композиции (62), независимость случайных величин  между собой и следующие свойства операции дисперсии: между собой и следующие свойства операции дисперсии:
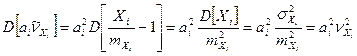
получим
 . (64) . (64)
Следовательно, величина вариации эксплуатационного показателя качества 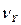 зависит от коэффициентов вариации показателей качества зависит от коэффициентов вариации показателей качества  изготавливаемых составных частей изделия на всей цепи технологических операций технологического процесса. Вклад каждой такой составляющей в общую величину изготавливаемых составных частей изделия на всей цепи технологических операций технологического процесса. Вклад каждой такой составляющей в общую величину 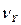 различен и определяется как величиной различен и определяется как величиной  так и величиной весового множителя так и величиной весового множителя  , который определяется производной (63). , который определяется производной (63).
Таким образом, при выполнении технологического процесса изготовления некоторого изделия будет получено значение одного из его эксплуатационных показателей Y в виде соотношения (59) для определения математического ожидания, соотношения (64) для определения коэффициента вариации показателя и соотношения  для определения диапазона его рассеивания. Проведение расчётов по полученным соотношениям обычно является сложной задачей, связанной с определением функциональной зависимости (58) эксплуатационного показателя от значений технологических показателей качества (геометрических размеров, шероховатости, твёрдости, показателей прочности и т.д.), получаемых на всех технологических операциях его изготовления. Однако, существующие некоторые частные математические модели, а также методы планирования эксперимента позволяют получить такую зависимость по крайней мере в виде уравнения регрессии. для определения диапазона его рассеивания. Проведение расчётов по полученным соотношениям обычно является сложной задачей, связанной с определением функциональной зависимости (58) эксплуатационного показателя от значений технологических показателей качества (геометрических размеров, шероховатости, твёрдости, показателей прочности и т.д.), получаемых на всех технологических операциях его изготовления. Однако, существующие некоторые частные математические модели, а также методы планирования эксперимента позволяют получить такую зависимость по крайней мере в виде уравнения регрессии.
Вместе с этим полученные соотношения играют важную роль в понимании методологии влияния технологических процессов на безотказность и долговечность изделий. Действительно, вероятность безотказной работы по некоторому эксплуатационному показателю (56) зависит не только от математического ожидания этого показателя, выбранного значения коэффициента запаса надёжности (57), но и коэффициента его вариации, величина которого (64) зависит от коэффициентов вариации технологических показателей качества составных частей изделия и его самого, получаемых на всех технологических операциях изготовления изделия. Причём их вклад определяется не только величиной коэффициента вариации  , но и весовым множителем , но и весовым множителем  в (64), который определяется производной (63). в (64), который определяется производной (63).
Для рациональной регламентации технологического процесса технологические показатели  задаются в нормативно-технической документации на изготовление номинальным значением задаются в нормативно-технической документации на изготовление номинальным значением  и допуском ∆Di. Однако, в свою очередь, эти технологические показатели и допуском ∆Di. Однако, в свою очередь, эти технологические показатели  зависят от показателей технологических режимов обработки зависят от показателей технологических режимов обработки  изделия. Эти показатели режимов обработки, в свою очередь, являются центрированными случайными величинами с коэффициентами вариации, зависящими от вида и качества средств технологического оснащения, условий из применения на производсте, регулярности подналадки и технического обслуживания, точности выполнения ручных операций и т.д. Аналогично тому, как был проведён расчёт для соотношения (58) можно выполнить расчёт для функциональной зависимости изделия. Эти показатели режимов обработки, в свою очередь, являются центрированными случайными величинами с коэффициентами вариации, зависящими от вида и качества средств технологического оснащения, условий из применения на производсте, регулярности подналадки и технического обслуживания, точности выполнения ручных операций и т.д. Аналогично тому, как был проведён расчёт для соотношения (58) можно выполнить расчёт для функциональной зависимости  от от  и получить соотношения аналогичные (59) и (64) и выводами аналогичными выводам, сделанным в предыдущем абзаце этого параграфа. и получить соотношения аналогичные (59) и (64) и выводами аналогичными выводам, сделанным в предыдущем абзаце этого параграфа.
Таким образом, проведённый анализ показывает, что в общем случае, дисперсии и показателей качества всех деталей и сборочных единиц и дисперсии режимов обработки на каждой технологической операции дают вклад в дисперсию и коэффициент вариации эксплуатационного показателя качества 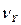 . Следовательно, с увеличением числа технологических операций, количества сборочных единиц, использования не достаточно жестких допусков на контролируемые параметры и параметры, которые подвергаются периодическому контролю, а также наличие ручных операций и возможность наличия параметров, которые дают существенный вклад, но не регламентируются документацией (например, часто радиусы сопряжений поверхности, величина и глубина залегания остаточных напряжений и т.д.) приводят к увеличению величины . Следовательно, с увеличением числа технологических операций, количества сборочных единиц, использования не достаточно жестких допусков на контролируемые параметры и параметры, которые подвергаются периодическому контролю, а также наличие ручных операций и возможность наличия параметров, которые дают существенный вклад, но не регламентируются документацией (например, часто радиусы сопряжений поверхности, величина и глубина залегания остаточных напряжений и т.д.) приводят к увеличению величины 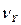 и необходимости использования больших значений коэффициентов безопасности n в расчетах на надежность (таблица 4). и необходимости использования больших значений коэффициентов безопасности n в расчетах на надежность (таблица 4).
Повышение качества продукции за счет снижения дисперсии показателей в процессе производства является одним из важнейших элементов технологической революции, прошедшей во всех ведущих странах мира.
|
 . В каждой технологической операции и в каждом технологическом переходе вследствие технологических воздействий происходит изменение формы, размеров и физико-механических свойств полуфабрикатов. Обозначим весь набор регламентированных НТД показателей на n-ой технологической операции изготовления k-ой детали через
. В каждой технологической операции и в каждом технологическом переходе вследствие технологических воздействий происходит изменение формы, размеров и физико-механических свойств полуфабрикатов. Обозначим весь набор регламентированных НТД показателей на n-ой технологической операции изготовления k-ой детали через  . Для дальнейшего удобства записи математических соотношений весь набор таких показателей качества изготовления для всех операций и всех полуфабрикатов и деталей представим в виде одного упорядоченного множества
. Для дальнейшего удобства записи математических соотношений весь набор таких показателей качества изготовления для всех операций и всех полуфабрикатов и деталей представим в виде одного упорядоченного множества  , где значение индекса i в определенном диапазоне соответствуют одной детали, а группа их значений в этом диапазоне соответствует определенному технологическому переходу или операции.
, где значение индекса i в определенном диапазоне соответствуют одной детали, а группа их значений в этом диапазоне соответствует определенному технологическому переходу или операции. . (58)
. (58) с величиной стандартных отклонений
с величиной стандартных отклонений  . Поэтому математическое ожидание эксплуатационного показателя качества Y в этих условиях будет определяться (п.4.5) соотношением:
. Поэтому математическое ожидание эксплуатационного показателя качества Y в этих условиях будет определяться (п.4.5) соотношением: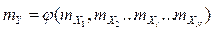 . (59)
. (59) от своих математических ожиданий. С точностью до первого порядка малости по таким отклонениям это разложение примет вид:
от своих математических ожиданий. С точностью до первого порядка малости по таким отклонениям это разложение примет вид: , (60)
, (60) ;
;  ;
; ;
;  . (61)
. (61) , (62)
, (62) . (63)
. (63) <<1 по их определению (61)), может быть получено как из физико-химических соображений (что является очень сложной задачей) или экспериментально, например, методом математического планирования эксперимента. Оно в принципе позволяет оценить относительную роль или вклад каждого показателя качества изготовления
<<1 по их определению (61)), может быть получено как из физико-химических соображений (что является очень сложной задачей) или экспериментально, например, методом математического планирования эксперимента. Оно в принципе позволяет оценить относительную роль или вклад каждого показателя качества изготовления  с коэффициентом вариации
с коэффициентом вариации 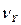 . Для этого можно воспользоваться соотношением (31), сделав предположение о нормальном законе распределения всех случайных величин, входящих в (62) или применить операцию вычисления дисперсии (9) к левой и правой частей соотношения (62).
. Для этого можно воспользоваться соотношением (31), сделав предположение о нормальном законе распределения всех случайных величин, входящих в (62) или применить операцию вычисления дисперсии (9) к левой и правой частей соотношения (62).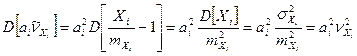
 . (64)
. (64) , который определяется производной (63).
, который определяется производной (63). для определения диапазона его рассеивания. Проведение расчётов по полученным соотношениям обычно является сложной задачей, связанной с определением функциональной зависимости (58) эксплуатационного показателя от значений технологических показателей качества (геометрических размеров, шероховатости, твёрдости, показателей прочности и т.д.), получаемых на всех технологических операциях его изготовления. Однако, существующие некоторые частные математические модели, а также методы планирования эксперимента позволяют получить такую зависимость по крайней мере в виде уравнения регрессии.
для определения диапазона его рассеивания. Проведение расчётов по полученным соотношениям обычно является сложной задачей, связанной с определением функциональной зависимости (58) эксплуатационного показателя от значений технологических показателей качества (геометрических размеров, шероховатости, твёрдости, показателей прочности и т.д.), получаемых на всех технологических операциях его изготовления. Однако, существующие некоторые частные математические модели, а также методы планирования эксперимента позволяют получить такую зависимость по крайней мере в виде уравнения регрессии. , но и весовым множителем
, но и весовым множителем  в (64), который определяется производной (63).
в (64), который определяется производной (63). изделия. Эти показатели режимов обработки, в свою очередь, являются центрированными случайными величинами с коэффициентами вариации, зависящими от вида и качества средств технологического оснащения, условий из применения на производсте, регулярности подналадки и технического обслуживания, точности выполнения ручных операций и т.д. Аналогично тому, как был проведён расчёт для соотношения (58) можно выполнить расчёт для функциональной зависимости
изделия. Эти показатели режимов обработки, в свою очередь, являются центрированными случайными величинами с коэффициентами вариации, зависящими от вида и качества средств технологического оснащения, условий из применения на производсте, регулярности подналадки и технического обслуживания, точности выполнения ручных операций и т.д. Аналогично тому, как был проведён расчёт для соотношения (58) можно выполнить расчёт для функциональной зависимости  и получить соотношения аналогичные (59) и (64) и выводами аналогичными выводам, сделанным в предыдущем абзаце этого параграфа.
и получить соотношения аналогичные (59) и (64) и выводами аналогичными выводам, сделанным в предыдущем абзаце этого параграфа.