|
|
Общая схема обоснования выбора показателей надежностиВыбор вида показателей надежности зависит от общего назначения изделия; ответственности выполняемых им функций; последствиями, возникающими при отказе изделия; экономическими соображениями и т.д. Основным показателем безотказности любого технического изделия является вероятность безотказной работы РH. Однако по мере эксплуатации изделия РH убывает. Поэтому вероятность безотказной работы связана с основным параметром долговечности – гамма-процентным ресурсом функциональной зависимостью Следовательно, задаваясь допустимыми изменениями РH в процессе эксплуатации, можно назначить Тg, при достижении которого изделие попадает в предельное состояние. После капитального ремонта и восстановления РH для изделия может быть назначено новое значение Тg,1. При последующей эксплуатации величина РH опять начинает снижаться и т.д. Обычно при каждом последующем ремонте число замененных узлов увеличивается N1<N2<N3<.... Эксплуатация изделия с ремонтами продолжается до тех пор, пока восстановление уровня надежности станет или невозможным, или невыгодным. Таким образом, возможны два варианта выбора показателей надежности. Первый вариант.При высоких требованиях к надежности изделия задаются допустимые значения g и по этому значению определяют гамма-процентный ресурс. Второй вариант.При обычных требованиях к надежности, когда отказ изделия не приводит к катастрофическим последствиям и большим экономическим потерям, задаются величиной Тg и по этому значению рассчитывают РH. Исходя из полученного значения назначают сроки плановых ремонтов и технического обслуживания таким образом, чтобы величина РH в межремонтный период лежала в приемлемых пределах. Однако и в первом, и во втором вариантах существуют предельные случаи, когда параметр безотказности РН перестает быть наглядным. Первый случай характерен для тех отказов, которые легко устранимы и не приводят к каким-либо значительным последствиям. Например, замена режущего инструмента при работе на станке, необходимость поправлять в транспортном лотке заклинившие детали и т.д. В этом случае характеристикой безотказности является параметр потока отказов. Другой крайний случай возникает при оценке высоконадежных изделий, когда значение PH(t) близко к единице. В этих случаях расчет производится по коэффициентам безопасности или коэффициентам запаса надежности. В теории надежности такой расчет обычно проводится как расчет вероятности безотказной работы изделия по заданному параметру. В связи с особой важностью этого вопроса рассмотрим его более подробно.
5.2 Основы параметрической теории надежности. Вероятность выполнения задания по параметру качества При расчетах на прочность, жесткость, износостойкость, теплостойкость, усталость, точность изготовления и т.д. проводится сопоставление по некоторым критериям расчетных параметров с их предельными значениями. Считают, что работоспособность по данному критерию обеспечена, если расчетный параметр критерия х меньше (или больше) заданного предельного значения хn. Учитывая требования надежности, в такой расчет вводят коэффициент безопасности п, принимая расчетное условие в виде:
В этом случае х и хп считают детерминированными величинами, хотя в действительности эти параметры являются статистическими и имеют определенное рассеивание. Для учета такого рассеивания расчет ведется по наиболее неблагоприятным значениям. Поэтому, хотя надежность и завышается по одному из критериев в ущерб другим, истинное значение показателя надежности неизвестно. Теория надежности позволяет корректно ответить на все возникающие в этой ситуации вопросы. Пусть задан некоторый параметр X, являющийся случайной величиной с плотностью распределения fx(x), и односторонний допуск Xп на этот параметр, также являющийся случайной величиной с плотностью распределения В этом случае вероятность выполнения задания определяется соотношением:
где, как обычно, детерминированная переменная l описывает область реализации случайной величины L. Пусть параметры X и Xn имеют нормальные законы распределения с числовыми характеристиками тх, sх и тп, sп. Используя устойчивость нормального закона к линейному преобразованию и вместо вычисления интегралов (49), используя (27) и (28), получим:
где ml =mx-mn, sl2=sx2+sn2, Up - квантиль нормального распределения. Введя коэффициент запаса надежности п=тх/тп и коэффициент вариации vx=sx/mx и vn=sn/mn, представим выражения для квантиля в виде:
Из соотношений (50) и (51) видно, что вероятность выполнения задания по параметру, вычисляемая для наиболее худшего случая L=0, зависит как от величины коэффициента запаса надежности, так и коэффициентов вариации параметра X и его предельного значения Xп. Например, пусть X - несущая способность детали, распределенная по нормальному закону с параметрами тх=3 kH и sх=0,7 kH, а Xn -действующая нагрузка, распределенная также по нормальному закону с параметрами тп=2 kH и sn=0,5 kH. Коэффициент запаса надежности будет тх/тn=1,5и, казалось бы, можно утверждать, что от этой нагрузки деталь не разрушится. Однако, расчет дает: Up= -1,16; Ф(-1,16)=-0,38 и РH(L=0)=0,88. Следовательно, мы получили, что хотя коэффициент запаса надежности выбран 1,5, тем не менее из каждых 100 деталей следует ожидать разрушение в 12 случаях. Такое низкое значение вероятности безотказной работы по параметру определяется наличием дисперсии (точнее величиной коэффициентов вариации) в распределениях как параметра, так и допуска на него. Видно, что даже в случае одинаковых коэффициентов запаса надежности можно получить различные вероятности выполнения задания в зависимости от рассеивания (дисперсии) случайной величины.
|
|
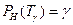 .
.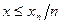 (или
(или 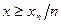 ) (48)
) (48)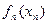 . Требуется определить вероятность выполнения задания по параметру X, т.е. вероятность того, что случайная величина L=X-Xn³0.
. Требуется определить вероятность выполнения задания по параметру X, т.е. вероятность того, что случайная величина L=X-Xn³0.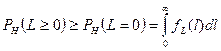 ,
,  , (49)
, (49)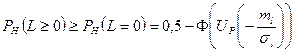 ,
, 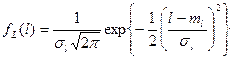 , (50)
, (50)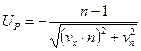 . (51)
. (51)