|
|
Нормальный закон распределения вероятностей случайных величинНаиболее широкое применение в теории вероятностей и различных ее прикладных приложениях, в том числе и в теории надежности, имеет нормальный закон распределения вероятностей случайных величин, которой является частным случаем распределения Вейбулла. Его широкое применение связано с удобством его прикладного применения (параметрами этого распределения являются математическое ожидание и дисперсия) и связано с центральной предельной теоремой теории вероятностей, суть которой сводится к следующему утверждению. Если некоторая случайная величина x является суммой большого числа независимых случайных величин xi Исходя из формулировки этой теоремы легко привести большое число примеров из различных областей знаний, когда априори можно утверждать, что некоторый рассматриваемый параметр имеет нормальное распределение. Нормальный закон распределения вероятностей некоторой случайной величины x, имеющей область возможных реализаций [а, в], имеет плотность распределения, определяемую следующим выражением:
где С – параметр, определяемый из условий нормировки ФРВ, Используя определение ФРВ и ее связь с плотностью распределения получим:
Подставляя в (21) выражение (20) и проведя необходимые преобразования получим:
где – Используя условия нормировки ФРВ
Интеграл ошибок Если множество возможных реализаций случайной величины x совпадает с действительной осью, то есть нижняя граница Нормальное распределение также используется для описания распределения случайной величины Т – наработки до отказа, имеющей область возможных реализаций [0, ¥]. Подставляя значения верхней и нижней границ в интеграл ошибок (
В таблице 2 приведены численные значения интеграла ошибок и константы С (25) в зависимости от значения параметра
Таблица 2 - Численные значения интеграла ошибок и нормировочной константы для ФРВ отказов в зависимости от параметра
Из таблицы 2 видно, что только при
Отметим, что во многих учебниках по надежности ФРВ отказов используют в виде (26) и (20) с С=1 без указания, что это приближенный вид распределения, а величина допускаемой погрешности зависит от коэффициента вариации этого параметра Из соотношения (26) следует, что в этом случае функцию распределения вероятности безотказной работы можно представить в виде:
где выражение для квантиля распределения имеет вид:
Нормальное распределение вероятности случайной величины двухпараметрическое распределение, содержащие в явном виде в качестве параметров m – математическое ожидание и s – стандартное отклонение случайной величины. Общий вид графиков нармального распределения приведён на рисунке 7. Нормальное распределение случайной величины обладает важным свойством, которое называется устойчивостью нормального распределения. Суть этого свойства сводится к следующему. Если случайная величина x является линейной композицией других случайных величин xi
(здесь аi и a0 – детерминированные величины), распределенных по нормальному закону с параметрами распределения
и стандартным отклонением:
Рисунок 7 - Плотность распределения f(t), ФРВ отказов F(t), ФРВ безотказной работы Рн (t) и интенсивность отказов нормального распределения в зависимости от наработки t для
Это свойство нормального распределения широко используется в теории надежности и других прикладных приложениях теории вероятности, например, при оценке производственных погрешностей, в управлении качеством продукции и т.п. Кроме того, при малых значениях коэффициента вариации нормальное распределение хорошо аппроксимирует биноминальное, Пуассоново и логарифмическое нормальное распределение. Основные виды непрерывных распределений случайной величины, используемых в теории надежности, представлены в табл.3. В таблице использовано общепринятое обозначение: Логарифмическое нормальное распределение (№3 таблица 3) используют для описания наработки до отказа деталей по усталости. Распределение Вейбулла (№4 таблица 3) обладает большой универсальностью, так как путем варьирования параметров t0(параметр масштаба) и т (параметр формы) переходит в другие виды распределения. Его используют для описания надежности изделий по приработочным отказам и усталостным разрушениям. Распределение c2(№6 таблица 3) в основном используется для оценки границ доверительных интервалов и проверки правдоподобия гипотез. Распределение Стьюдента (№7 таблица 3) применяют для оценки границ доверительных интервалов при конечном числе измерений.
|
|
 и если среди слагаемых xi нет таких, влияние которых на дисперсию x является преобладающим (или проще – нет отдельных слагаемых xi величина которых сравнима с величиной суммы x), то при неограниченном возрастании числа слагаемых закон распределения вероятности случайной величины x все с более высокой точностью приближается к нормальному закону вне зависимости от того каким законом распределения подчиняются слагаемые xi.
и если среди слагаемых xi нет таких, влияние которых на дисперсию x является преобладающим (или проще – нет отдельных слагаемых xi величина которых сравнима с величиной суммы x), то при неограниченном возрастании числа слагаемых закон распределения вероятности случайной величины x все с более высокой точностью приближается к нормальному закону вне зависимости от того каким законом распределения подчиняются слагаемые xi. , (20)
, (20) и
и  – математическое ожидание и стандартное отклонение случайной величины.
– математическое ожидание и стандартное отклонение случайной величины. <
<  . (21)
. (21) , (22)
, (22) – интеграл ошибок или интеграл Лапласа,
– интеграл ошибок или интеграл Лапласа,  – квантиль нормального распределения.
– квантиль нормального распределения. , заключающиеся в выполнении условия
, заключающиеся в выполнении условия  , получим в явном виде выражение для нормировочной константы:
, получим в явном виде выражение для нормировочной константы: . (23)
. (23) , через который выражается в явном виде ФРВ
, через который выражается в явном виде ФРВ  – является нечетной функцией;
– является нечетной функцией;  ;
;  – интеграл Пуассона.
– интеграл Пуассона. , а верхняя –
, а верхняя – 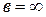 , то
, то  и
и  и
и  , то
, то  , а
, а 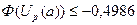 и величина константы С отличается от 1 на величину меньшую 0,0028. Следовательно, в этом случае можно использовать упрощенный вид функций (20) и (22) с
и величина константы С отличается от 1 на величину меньшую 0,0028. Следовательно, в этом случае можно использовать упрощенный вид функций (20) и (22) с  , допуская погрешность меньшую 0,3%.
, допуская погрешность меньшую 0,3%. и
и  ) получим выражение для ФРВ отказов (22) и (23) в виде:
) получим выражение для ФРВ отказов (22) и (23) в виде: , (24)
, (24) . (25)
. (25)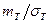 .
.
 с погрешностью менее 0,1% функцию распределения вероятности отказов можно записать в виде:
с погрешностью менее 0,1% функцию распределения вероятности отказов можно записать в виде: , (26)
, (26) . Причём в надёжности значение этого параметра существенно больше, чем при оценке геометрической точности изготовления.
. Причём в надёжности значение этого параметра существенно больше, чем при оценке геометрической точности изготовления.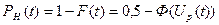 , (27)
, (27) . (28)
. (28) , (29)
, (29) и
и  , то случайная величина x распределена также по нормальному закону с математическим ожиданием:
, то случайная величина x распределена также по нормальному закону с математическим ожиданием: , (30)
, (30) . (31)
. (31)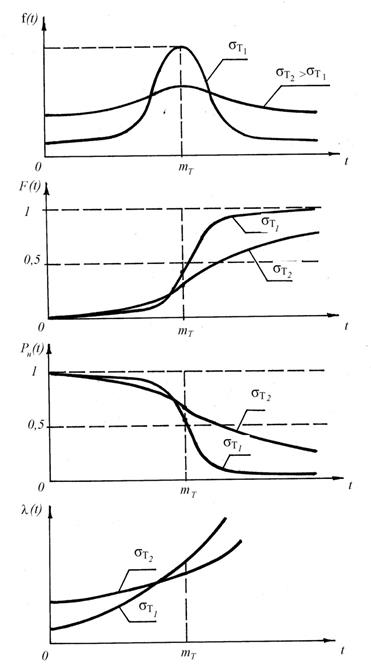
 >
> 
 - гамма-функция.
- гамма-функция.