|
|
Лабораторная работа №2.2.2. Определение молекулярной массы и плотности воздуха методом откачки
Цель работы: нахождение значения молекулярной массы и плотности воздуха. Приборы и принадлежности: лабораторная установка ФПТ 1-12, стеклянная колба с краником, лабораторные весы. Задачи работы: Изучить понятие состояния идеального газа и уравнение Менделеева-Клапейрона. Понять суть нормального атмосферного давления. Познакомиться с разреженным состоянием газа и с вакуумной техникой. Краткая теория В механике решается задача, в которой определяется положение тела в пространстве в любой момент времени. Для решения этой задачи применяется второй закон Ньютона, законы сохранения и основные теоремы динамики. Применение этих законов для решения конкретных задач требует задания начальных условий. Чаще всего, в роли начальных условий задаются координаты тела, и его скорость в начальный момент времени. В процессе применения названных законов механики также определяются координаты, и скорость в любой момент времени. Именно поэтому для описания состояния тела в механике необходимо указать его скорость или импульс и координаты в указанный момент времени. В молекулярной физике основное внимание уделяется описанию поведения тела и его свойств на основе его внутреннего строения. В настоящее время строение тела постулируется основными положениями молекулярно-кинетической теории. Согласно этой теории, все материальные объекты любой природы состоят из частиц. Этими частицами могут быть молекулы, ионы, атомы, электроны, фотоны и другие, известные в настоящее время частицы. В настоящее время известны размеры этих частиц, их массы и другие физические характеристики. На основе этих данных легко определяется число частиц в составе того или иного тела. Число таких частиц огромно по сравнению с числом тел, которые рассматриваются в механических задачах. Количественно число частиц в теле или системе сравнивается с фундаментальной величиной, которой является число Авогадро. Число Авогадро показывает, какое количество частиц содержится в одном моле любого вещества. Это число определено в опытах Перрена, оно является одной из фундаментальных постоянных в физике. Число Авогадро равно:
Тела, содержащие число частиц, сравнимое с числом Авогадро, называются макроскопическими системами. К таким системам относятся окружающие нас тела и вещества. Ясно, что описать состояние такой системы с помощью механики невозможно. Это связано не только с тем, что механическая задача потребует решения системы огромного числа векторных дифференциальных уравнений второго порядка, но главным образом с тем, что в силу хаотического движения частиц в макроскопических системах невозможно задать начальные условия. Невозможность описать состояние макроскопической системы механическими величинами становится очевидной при учете волновых свойств микрочастиц, из которых состоят тела. Хаотическое движение частиц макроскопической системы, а также их волновые свойства приводят к тому, что состояние таких систем можно описать только с помощью некоторых средних величин. Таким величинами являются объем тела или системы, давление и температура. Объем Следующей характеристикой состояния макроскопической системы является давление Следующей характеристикой состояния макроскопической системы является температура Температура Задание объема, давления и температуры макроскопической системы позволяют описать свойства системы, они заменяют задание координат и импульсов всех частиц системы. Поэтому эти величины называются параметрами состояния макроскопической системы. Уравнение, в котором описывается связь между параметрами состояния, называется уравнением состояния. Уравнение состояния можно записать в общем виде:
Для каждой макроскопической системы уравнение состояния будет принимать конкретный вид. Его можно вывести различными способами. Например, его можно получить, анализируя процессы в системе, или с использованием законов термодинамики, или на основе законов поведения отдельных частиц системы. Исторически первым было получено уравнение состояния идеального газа. При этом использовались полученные на опытах законы процессов, протекающих в идеальном газе. Сначала учеными был изучен изотермический процесс в газе. Изотермическим процессом называется процесс, при котором температура газа, состав газа и его масса не изменяются в ходе всего процесса. В 1661 году английский физик и химик Роберт Бойль, а в 1676 году французский физик Эдм Мариотт исследовали зависимость давления газа
Этот закон называется законом Бойля – Мариотта. В 1727 году французский физик Жак Шарль исследовал зависимость изменения давления от температуры при постоянном объеме. Процесс, в котором при неизменном составе газа и неизменной массе газа объем газа остается постоянным называется изохорическим. На опытах Ж.Шарль установил, что в изохорическом процессе давление изменяется с температурой по линейному закону:
В формуле (3)
В формуле (4) в числителе стоит изменение давления, а в знаменателе изменение температуры, так как начальная температура выбрана за ноль градусов Цельсия. Поэтому в общем виде термический коэффициент давления определяется формулой:
Из последней формулы следует, что термический коэффициент давления показывает, на какую величину изменяется единица давления газа при изменении его температуры на единицу. Эта величина имеет размерность:
Как видно из формулы (5), величину термического коэффициента давления можно легко измерить. При этом оказалось, что для большинства газов и для воздуха, представляющего собой смесь газов, значение термического коэффициента давления принимает одинаковое значение, равное
Последняя формула позволяет ввести новую температурную шкалу, для которой выполняется следующее соотношение:
Такая шкала была введена в 1848 году английским физиком В. Кельвином. Она называется шкалой Кельвина, а единица температуры называется кельвин. Из формулы (7) следует, что начало отсчета по шкале Кельвина или ноль кельвин по шкале Цельсия совпадает с температурой
В 1802 году французский химик Ж.Гей-Люссак исследовал изобарический процесс. Изобарический процесс представляет собой изменение объема газа при изменении его температуры, если давление газа, его состав и масса не изменяются. При этом он получил, что для всех газов объем линейно возрастает с температурой по закону:
В этой формуле
Коэффициент объемного расширения показывает, на какую величину изменится единица объема тела или газа при изменении температуры на единицу. Эта величина легко измеряется на опыте и, как показал Гей-Люссак, для всех газов она с большой степенью точности равна величине:
Это позволяет использовать для изобарического процесса температурную шкалу Кельвина. Тогда закон Гей-Люссака можно записать в виде: Используя законы изопроцессов, французский физик Б.Клапейрон в 1834 году вывел уравнение состояния идеального газа. Для того чтобы вывести уравнение Клапейрона, изобразим в системе координат Можно выбрать различные пути перехода из состояния
Здесь
Рис.1. Иллюстрация к выводу уравнения Клапейрона
Процесс
Перемножим, левые и правые части уравнений (13) и (14). При этом объем
Это уравнение является уравнением состояния газа или уравнением Клапейрона. Сущность этого уравнения состоит в том, что при неизменном составе газа и при постоянной массе газа его параметры состояния связаны условием:
Это уравнение можно получить, используя другие переходы из состояния Чтобы вычислить эту постоянную величину const, необходимо выделить какие-то условия существования газа. Такие условия называются нормальными условиями. Нормальным условиям соответствует давление газа, равное одной атмосфере, и температура, равная нулю градусов Цельсия:
Теперь необходимо определить объем некоторой стандартной массы газа. При этом использовался закон Авогадро. В 1811 году итальянский физик Авогадро показал, что в равных объемах различных газов при одинаковых давлениях и температурах содержится одинаковое число частиц. Это позволило за стандартную массу газа выбрать один моль газа. На опыте было измерено, что при нормальных условиях (17) один моль любого газа имеет объем
Теперь можем вычислить константу в уравнении Клапейрона для одного моля любого газа:
Эта величина называется универсальной газовой постоянной. Теперь можно записать уравнение состояния для одного моля газа:
Из этого уравнения можно легко перейти к уравнению состояния для любой массы газа или для любого объема газа. Пусть имеем произвольный объем газа
Теперь подставим этот объем в формулу (20), тогда получим:
Если известно число частиц в газе
Тогда уравнение состояния газа будет иметь вид:
В формулу (24) входят две постоянные величины
Эта величина была введена Л.Больцманом и называется постоянной Больцмана. Теперь уравнение состояния газа можно записать в виде:
Здесь Если известна масса газа
Подставим эту формулу в уравнение (22), тогда уравнение состояния газа будет иметь вид:
Это уравнение было получено Д.И.Менделеевым, после этих преобразований уравнение состояния газа стали называть уравнением Менделеева – Клапейрона. Все параметры газа, входящие в уравнение (28), можно измерить непосредственно, за исключением массы газа, т.к. взвешивание газа возможно только вместе с сосудом, в который он заключен, поэтому для определения массы газа (т) необходимо исключить массу сосуда. Это можно сделать, рассмотрев два состояния одного и того же газа при неизменных температуре (Т) и объеме (V). Пусть в первом состоянии масса газа Записав уравнение (28) для двух состояний газа (до откачки и после), получаем систему из двух уравнений, решение которой дает выражение для универсальной газовой постоянной:
Таким образом, для определения молекулярной массы воздуха необходимо на эксперименте определить разницу масс в колбе до откачки и после откачки, а также Плотность воздуха можно легко рассчитать из уравнения Менделеева-Клапейрона
Описание работы установки Лабораторная установка состоит из блока ФПТ 1-12 (1), стеклянной колбы, объёмом один литр (4), и соединяющего их резинного шланга. Также в оснастку лабораторной работы входят электронные весы (3) и термометр, табло которого выведено на переднюю панель. Внутри блока (1) смонтирован микрокомпрессор (2), который позволяет откачивать из колбы (4) воздух через шланг. Блок (1) включается переключателем «Сеть». Микрокомпрессор работает, когда зажата кнопка «Пуск». Давление в колбе можно контролировать по показаниям манометра «Давление». Когда давление в колбе равно атмосферному, то манометр показывает ноль. Это соответствует 100 000 Па. Когда из колбы откачана часть воздуха, то манометр показывает разницу давлений внутри и вне колбы. Манометр проградуирован так, что его показания в точности показывают, какая доля воздуха была откачана из колбы. Если бы из колбы был откачан весь воздух, то манометр показал бы минус единицу. Реально не удаётся откачать больше, чем 95% воздуха. При этом стрелка манометра указывает на - 0,95 бар. Это соответствует 100 000 Па
Рис. 2. Общий вид экспериментальной установки ФПТ1-12: 1 – корпус измерительного блока; 2 – компрессор; 3 – весы; 4 – колба; 5 – стойка; 6 – вакуумметр, 7 – кран.
Порядок выполнения работы 1. Включите весы, аккуратно отсоедините колбу от шланга, откройте краник на колбе. Теперь взвесьте колбу на весах. Полученное значение запишите в первую строку таблицы 1 как 2. Включите установку ФПТ 1-12 кнопкой «Сеть». Запишите значение температуры с табло «Температура» в первую строку таблицы 1. Обязательно переведите это значение из градусов Цельсия в градусы кельвина. 3. Подсоедините шланг к колбе (краник всё еще открыт). Теперь зажмите кнопку «Пуск». Компрессор начинает гудеть и откачивать из колбы воздух. Продолжайте откачивать, пока манометр не покажет - 0,95 бар. Иногда стрелка застревает. Просто продолжайте откачивать воздух. 4. Перекройте краник. Аккуратно отсоедините колбу от шланга. Взвесьте колбу на весах. Полученное значение запишите в первую строку таблицы 1 как 5. Теперь откройте краник, воздух с шипением наполнит колбу. 6. Заполните оставшиеся ячейки первой строки таблицы 1. Не забудьте перевести массу из грамм в килограммы. Рассчитайте молекулярную массу 7. Повторите пункты 1-4, заполняя оставшиеся строки таблицы 1. Таблица 1.
Контрольные вопросы 1. Какими величинами описывается состояние тела в механике? 2. Какие законы механики позволяют определить величины, описывающие состояние тела в механике? 3. Сформулируйте основные положения молекулярно-кинетической теории строения вещества. 4. Что понимается под атомом? Молекулой? 5. Что называется относительной атомной (молекулярной) массой? 6. Какова масса атомов? Как ее можно рассчитать? 7. Как определить размер атома? 8. Что называется молем вещества? 9. Что показывает число Авогадро? Чему равно число Авогадро? 10. Что называется молярной массой вещества? 11. Какая существует связь между собой относительная атомная масса и молярная масса? 12. Что называется макроскопической системой? 13. Какие величины описывают состояние макроскопической системы? 14. Почему нельзя описывать состояние макроскопической системы механическими методами? 15. Дайте определения и охарактеризуйте все параметры состояния макроскопической системы. 16. Запишите законы изотермического процесса. Изобразите графики этого процесса в различных системах координат: 17. Запишите законы изохорического процесса. Изобразите графики этого процесса в различных системах координат: 18. Что называется термическим коэффициентом давления? 19. Как осуществляется переход от температурной шкалы в градусах Цельсия к температурной шкале в кельвинах? 20. Запишите законы изобарического процесса. Изобразите графики этого процесса в различных системах координат: 21. Что называется коэффициентом объемного расширения? Чему он равен для газов? 22. Выведите уравнение Клапейрона для газов. 23. Какие условия называются нормальными условиями? 24. Вычислите универсальную газовую постоянную. Используя нормальные условия. 25. Выведите различные выражения для уравнения состояния идеального газа. 26. Что называется постоянной Больцмана? Чему она равна? 27. Вывести рабочую формулу для измерения молекулярной массы воздуха. 28. Поясните, какие измерения надо сделать в работе. Как выполнить эти измерения. 29. Поясните, как производится измерение массы откачанного воздуха.
2.3. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
|
|
 .
. , как характеристика состояния макроскопической системы, имеет такой же смысл, как и объем тела в механике. В механике под объемом тела понимается объем той части пространства, которая занята этим телом. В молекулярной физике понятие объема уточняется тем, что обязательно фиксируется тот факт, что объем тела всегда показывает его границы с внешними телами. У газов есть свойство занимать весь предоставленный им объём. Газ мог находиться в колбе с объёмом 1 л. Тогда его объём будет равен 1л. Если тот же газ переместить в колбу объёмом 100 л, то газ расширится и станет занимать 100 л. Конечно, газ не может расширяться бесконечно. В безграничных просторах космоса газ собирается в облака конечного объёма. Но в условиях земли можно смело считать, что объём газа равен объёму сосуда, в котором он находится.
, как характеристика состояния макроскопической системы, имеет такой же смысл, как и объем тела в механике. В механике под объемом тела понимается объем той части пространства, которая занята этим телом. В молекулярной физике понятие объема уточняется тем, что обязательно фиксируется тот факт, что объем тела всегда показывает его границы с внешними телами. У газов есть свойство занимать весь предоставленный им объём. Газ мог находиться в колбе с объёмом 1 л. Тогда его объём будет равен 1л. Если тот же газ переместить в колбу объёмом 100 л, то газ расширится и станет занимать 100 л. Конечно, газ не может расширяться бесконечно. В безграничных просторах космоса газ собирается в облака конечного объёма. Но в условиях земли можно смело считать, что объём газа равен объёму сосуда, в котором он находится. . Это понятие также заимствуется из механики. В механике под давлением понимается скалярная величина, равная отношению силы, действующей на некоторую площадь, к величине этой площади. В механике показывается, что можно рассматривать два вида давления. Давление может быть статическим и динамическим. Статическое давление производят неподвижные тела на поверхность тел, с которыми они взаимодействуют. Динамическое давление – это давление, которое оказывают на некоторую поверхность ударяющиеся об нее движущиеся тела. Из такого объяснения и особенностей поведения частиц макроскопической системы следует, что давление в молекулярной физике определяется ударами хаотически движущихся частиц о стенки сосудов. Такое давление является динамическим давлением, и измерить можно только некоторое среднее значение давления, так как количество ударяющихся о некоторую поверхность частиц огромно, а сила, с которой каждая частица действует на поверхность, неизвестна и носит случайный характер.
. Это понятие также заимствуется из механики. В механике под давлением понимается скалярная величина, равная отношению силы, действующей на некоторую площадь, к величине этой площади. В механике показывается, что можно рассматривать два вида давления. Давление может быть статическим и динамическим. Статическое давление производят неподвижные тела на поверхность тел, с которыми они взаимодействуют. Динамическое давление – это давление, которое оказывают на некоторую поверхность ударяющиеся об нее движущиеся тела. Из такого объяснения и особенностей поведения частиц макроскопической системы следует, что давление в молекулярной физике определяется ударами хаотически движущихся частиц о стенки сосудов. Такое давление является динамическим давлением, и измерить можно только некоторое среднее значение давления, так как количество ударяющихся о некоторую поверхность частиц огромно, а сила, с которой каждая частица действует на поверхность, неизвестна и носит случайный характер. . В настоящее время под температурой понимается количественная характеристика термодинамического равновесия изучаемой макроскопической системы с другими телами и системами. Первоначально понятие температуры вводилось на основе ощущений тепла и холода. Именно отсюда пошли известные в настоящее время эмпирические температурные шкалы. Примером такой эмпирической температурной шкалы является шкала Цельсия или шкала Реомюра, или шкала Фаренгейта. Такие температурные шкалы и соответствующие им возможности измерения температуры использовались для исследования свойств различных тел на опыте.
. В настоящее время под температурой понимается количественная характеристика термодинамического равновесия изучаемой макроскопической системы с другими телами и системами. Первоначально понятие температуры вводилось на основе ощущений тепла и холода. Именно отсюда пошли известные в настоящее время эмпирические температурные шкалы. Примером такой эмпирической температурной шкалы является шкала Цельсия или шкала Реомюра, или шкала Фаренгейта. Такие температурные шкалы и соответствующие им возможности измерения температуры использовались для исследования свойств различных тел на опыте. определяет скорости, с которыми движутся молекулы этого газа. Чем выше температура, тем с большими скоростями летят молекулы. Например, мы прикладываем руку к стакану с тёплой водой. Молекулы воды движутся с большими скоростями, чем молекулы руки и стакана. Молекулы воды, сталкиваясь с молекулами стакана, передают им часть своей энергии. Молекулы стакана начинают двигаться быстрее, стакан нагревается. Вода, кстати, при этом немного остывает. Молекулы стакана в свою очередь бьются о молекулы кожи руки и молекулы руки тоже приобретают дополнительную энергию движения. Рука нагревается от стакана. Молекулы руки передают увеличившуюся энергию молекулам нервных окончаний, а нервные окончания передают электрические сигналы в мозг и мозг понимает, что рука прикоснулась к тёплому стакану, а не к холодному. Температура в молекулярной физике измеряется в градусах кельвина. Температура в градусах кельвина связана с температурой в градусах цельсия следующим соотношением
определяет скорости, с которыми движутся молекулы этого газа. Чем выше температура, тем с большими скоростями летят молекулы. Например, мы прикладываем руку к стакану с тёплой водой. Молекулы воды движутся с большими скоростями, чем молекулы руки и стакана. Молекулы воды, сталкиваясь с молекулами стакана, передают им часть своей энергии. Молекулы стакана начинают двигаться быстрее, стакан нагревается. Вода, кстати, при этом немного остывает. Молекулы стакана в свою очередь бьются о молекулы кожи руки и молекулы руки тоже приобретают дополнительную энергию движения. Рука нагревается от стакана. Молекулы руки передают увеличившуюся энергию молекулам нервных окончаний, а нервные окончания передают электрические сигналы в мозг и мозг понимает, что рука прикоснулась к тёплому стакану, а не к холодному. Температура в молекулярной физике измеряется в градусах кельвина. Температура в градусах кельвина связана с температурой в градусах цельсия следующим соотношением  .
. (1)
(1) от его объема
от его объема  при постоянной температуре. При этом они установили, что в этом процессе произведение давления на объем сохраняется, то есть:
при постоянной температуре. При этом они установили, что в этом процессе произведение давления на объем сохраняется, то есть: или
или  , если
, если  (2)
(2)
 (3)
(3) - давление газа при некоторой температуре
- давление газа при некоторой температуре  , измеренной по эмпирической температурной шкале Цельсия,
, измеренной по эмпирической температурной шкале Цельсия,  - давление газа при температуре
- давление газа при температуре  ,
,  - термический коэффициент давления. Этот закон называется законом Шарля. Из формулы (3) следует, что
- термический коэффициент давления. Этот закон называется законом Шарля. Из формулы (3) следует, что (4)
(4) (5)
(5)
 . Подставим это значение
. Подставим это значение  (6)
(6) (7)
(7) , а ноль градусов по шкале Цельсия совпадает с температурой
, а ноль градусов по шкале Цельсия совпадает с температурой  по шкале Кельвина. Тогда формула (6) будет иметь вид:
по шкале Кельвина. Тогда формула (6) будет иметь вид: или
или  при
при  (8)
(8) (9)
(9) - объем газа при некоторой температуре
- объем газа при некоторой температуре  , измеренной по шкале Цельсия,
, измеренной по шкале Цельсия,  - объем газа при температуре, равной нулю градусов по Цельсию,
- объем газа при температуре, равной нулю градусов по Цельсию,  - коэффициент объемного расширения. Этот закон называется законом Гей-Люссака. Величина коэффициента объемного расширения определяется по формуле:
- коэффициент объемного расширения. Этот закон называется законом Гей-Люссака. Величина коэффициента объемного расширения определяется по формуле: (10)
(10) . (11)
. (11) или
или  при
при  (12)
(12) на рисунке 1 две изотермы. Пусть точка
на рисунке 1 две изотермы. Пусть точка  изображает некоторое исходное состояние газа. В этом состоянии газ имеет следующие параметры состояния -
изображает некоторое исходное состояние газа. В этом состоянии газ имеет следующие параметры состояния -  . Пусть точка
. Пусть точка  изображает некоторое конечное состояние этого же газа с параметрами состояния -
изображает некоторое конечное состояние этого же газа с параметрами состояния -  найдем уравнение связи между этими параметрами состояния. Для решения этой задачи воспользуемся сформулированными газовыми законами.
найдем уравнение связи между этими параметрами состояния. Для решения этой задачи воспользуемся сформулированными газовыми законами. в соответствии с рисунком 1. При этом процесс
в соответствии с рисунком 1. При этом процесс  изотермический, протекающий при температуре
изотермический, протекающий при температуре  . Для этого процесса можно записать:
. Для этого процесса можно записать: (13)
(13) - давление газа в состоянии
- давление газа в состоянии  , равное давлению газа в конечном состоянии
, равное давлению газа в конечном состоянии  - объем газа в состоянии
- объем газа в состоянии 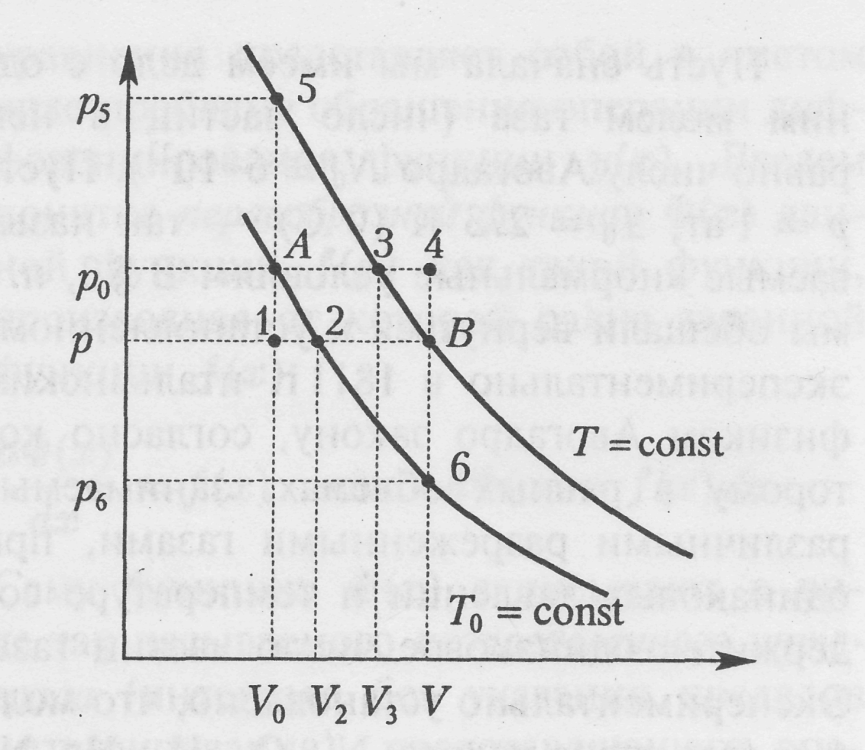
 является изобарическим при постоянном давлении
является изобарическим при постоянном давлении  . Для этого процесса можно записать уравнение:
. Для этого процесса можно записать уравнение: (14)
(14) (15)
(15) (16)
(16) . Эти переходы необходимо рассмотреть самостоятельно.
. Эти переходы необходимо рассмотреть самостоятельно. ,
,  (17)
(17) (18)
(18) (19)
(19) (20)
(20) и знаем, что этот объем занимают
и знаем, что этот объем занимают  молей газа. Тогда можем найти объем одного моля:
молей газа. Тогда можем найти объем одного моля: (21)
(21) или
или  (22)
(22) , то число молей
, то число молей  (23)
(23) (24)
(24) и
и  . Их можно заменить одной величиной, которая также будет постоянной для всех газов:
. Их можно заменить одной величиной, которая также будет постоянной для всех газов: (25)
(25) или
или  (26)
(26) - концентрация частиц или число частиц в единице объема.
- концентрация частиц или число частиц в единице объема. и его молярная масса
и его молярная масса  , тогда число молей газа можно найти по формуле:
, тогда число молей газа можно найти по формуле: (27)
(27) (28)
(28) , а во втором
, а во втором  . Масса сосуда с воздухом в первом состоянии
. Масса сосуда с воздухом в первом состоянии  , где т0— масса сосуда, а масса сосуда во втором состоянии
, где т0— масса сосуда, а масса сосуда во втором состоянии  , очевидно, что
, очевидно, что  .
. (29).
(29). .
. (30).
(30). 0,05% = 5 000 Па.
0,05% = 5 000 Па.

 .
. .
. по формуле (2.29). Рассчитайте плотность воздуха
по формуле (2.29). Рассчитайте плотность воздуха  считая
считая  по формуле (2.30).
по формуле (2.30). , м3
, м3
 , г
, г
 , г
, г
 , кг
, кг
 , кг/моль
, кг/моль
 , кг/м3
, кг/м3
