|
|
Лабораторная работа №2.1.5. Изучение собственных колебаний струныЦель работы: получение на струне стоячих волн, наблюдение картины распределения амплитуд и количественная проверка формулы собственных частот колебаний струны. Оборудование: 1) генератор электрических колебаний (измерительное устройство); 2) струна на подставке.
Теоретические сведения. Если натянутую между двумя точками струну вывести из положения равновесия, она будет совершать колебания. Волна, распространяясь по струне, отражается от ее концов. Вследствие наложения падающей и отраженной волн в струне устанавливаются особые колебания Особенности состоят в том, что колеблются не все точки струны. Часть из них остаются неподвижными и называются узлами стоячей волны. На концах струны в точках закрепления обязательно получаются узлы, а между ними одна или несколько пучностей – областей, колеблющихся с максимальной амплитудой. Между двумя соседними узлами все точки струны колеблются одновременно (в одинаковой фазе, синфазно), но с разными амплитудами. Такой тип синфазных колебаний с характерным пространственным распределением амплитуд – чередованием узлов (нулей) и пучностей (максимумов) получил название стоячей волны. Расстояние между двумя соседними узлами равно половине длины волны. Все точки, находящиеся между соседними узлами, одновременно достигают максимального отклонения и одновременно проходят через положение равновесия. На рис. 1 даны «моментальные фотографии» отклонений точек от положения равновесия в два близких момента времени
Рис. 1. Колебания струны На рис. 2 показаны положения струны через каждую восьмую часть периода 8 T . Вначале все точки струны лежат на прямой линии (см. рисунок). Затем между неподвижными узлами происходит вспучивание струны, которое достигает максимума через четверть периода. После этого вспучивание спадает, и струна снова становится прямой через пол периода. Далее вспучивание происходит в другую сторону. В каждое мгновение видна волна, при этом волна стоит на месте – отсюда название этого типа колебаний – стоячая волна. Другие примеры стоячих волн – стоячая звуковая волна внутри воздушных труб (орган, духовые музыкальные инструменты), стоячие электромагнитные волны в линиях передач или волноводах. В отличие от бегущей волны, которая может двигаться вправо или влево, у стоячей волны нет направления распространения. Это отличие видно на двух снимках, относящихся к близким моментам времени (рис. 3). Для бегущей волны максимумы и минимумы волны в каждое следующее мгновение переходят на новое место, а в стоячей волне остаются на одном и том же месте. В стоячей волне в отличие от бегущей не происходит переноса энергии. Это объясняется тем, что падающая и отраженная волны имеют одинаковую амплитуду и поэтому переносят одинаковую энергию в противоположных направлениях. Т. к. узловые точки неподвижны, через них энергия не переносится. Энергия стоячей волны есть величина постоянная. В тот момент времени, когда все частицы струны проходят через положение равновесия, вся энергия колеблющихся частиц является кинетической. Наоборот, в положении максимального отклонения от положения равновесия, энергия всех частиц является потенциальной. Происходит превращение кинетической энергии в потенциальную и наоборот. На длине струны l будет укладываться всегда целое число стоячих волн. Отсюда вытекает условие:
Так как длина волны λ связана со скоростью распространения волны v и частотой колебания ν соотношением Струна, следовательно, может колебаться не с одной частотой, а с целым спектром частот. Частоты
которая называется основной частотой. Опыт показывает, что скорость распространения упругой волны вдоль струны определяется величиной натяжения Т струны и линейной плотности ρ материала струны (массой единицы длины струны)
Подставляя (5) в (3), получим формулу для расчета частот колебаний струны
Описание прибора
Рис. 4. Внешний вид установки
Прибор состоит из жесткой основы, на которой закреплены постоянные магниты, между полюсами которых натянута струна, и механизма натяжения струны. Один конец струны жестко закреплен, а другой прикреплен к тарировочной пружине. Второй конец пружины механически связан с винтовым механизмом, с помощью которого можно изменять натяжение струны. Сила натяжения струны измеряется с помощью показателя, который перемещается по шкале при изменении натяжения струны. В состав измерительного устройства входит генератор синусоидальных колебаний и частотомер. На передней панели устройства размещены: – ручки «ЧАСТОТА ГРУБО» и «ЧАСТОТА ТОЧНО» – для установки частоты генератора; – ручка «УРОВЕНЬ» для установки необходимой амплитуды выходного напряжения генератора (амплитуда колебаний струны); – жидкокристаллический дисплей. На струну с током действует магнитная сила, направленная перпендикулярно току. Поскольку ток переменный, то и сила изменяется с той же частотой и раскачивает струну. Частоту изменения силы можно изменять с помощью генератора. Когда частота магнитной силы становится близкой к частоте собственных колебаний струны, возникает резонанс, и колебания усиливаются.
Измерения. 1. Подключить установку в сеть 220 В. Нажать выключатель «СЕТЬ» устройства питания лампы подсвечивания (светится лампа). Нажать выключатель «СЕТЬ» измерительного устройства (светится подсвечивание дисплея и на дисплее отображается выставленная частота). 2. Дать установке прогреться 3-5 мин. 3. Установить натяжение струны 0,4 Н. Ручку «УРОВЕНЬ» установить в среднее положение. 4. Изменяя с помощью ручек «ЧАСТОТА ГРУБО» и «ЧАСТОТА ТОЧНО» Частоту в диапазоне 20-45 Гц, получить одну хорошо заметную волну на всей длине струны. 5. Увеличивая частоту, получить волны на других частотах. Максимальное число их не меньше четырех. 6. Записать показания генератора и зарисовать распределение амплитуд колебаний точек струны во всех случаях. 7. Повторить опыт при натяжении струны 0,3 Н. 9. По формуле (6) рассчитать частоты собственных колебаний для каждого случая и занести данные в таблицу 1. Таблица 1
Контрольные вопросы. 1. Что называется стоячей волной? Запишите формулу стоячей волны. 2. Что называется узлом (пучностью) стоячей волны? 3. Происходит ли в стоячей волне перемещение колебаний в пространстве (вдоль оси Х)? 4. Наступает ли такое состояние стоячей волны, когда все точки струны лежат на одной прямой? Будут ли при этом точки неподвижны? 5. Происходит ли перенос энергии в стоячей волне вдоль оси Х? 6. В каких фазах колеблются точки струны между двумя узлами? 7. В каких фазах колеблются точки струны лежащие по обе стороны одного и того же узла? 8. Как изменяется амплитуда колебаний между двумя узлами? 9. Чем отличается стоячая волна от бегущей? 10. Какие колебания струны называются собственными?
2.2. МОЛЕКУЛЯРНАЯ ФИЗИКА Лабораторная работа №2.2.1. Определение отношения Цель работы: – знакомство с одним из методов определения отношения теплоемкостей при постоянном давлении и постоянном объеме, – сравнение результатов эксперимента с теорией. Приборы и принадлежности: лабораторная установка ФПТI-6.
Краткая теория Элементарная теплота δQ связана с бесконечно малым изменением температуры dT следующим образом:
Величина C характеризует тепловые свойства тела и называется теплоемкостью. Теплоемкость численно равна количеству теплоты, необходимому для повышения температуры на 1 градус (Кельвин). Для характеристики тепловых свойств веществ существуют понятия удельной c и молярной C теплоемкости. Связь между ними выражается так:
где M — молярная масса. В газе различают теплоемкости: при постоянном давлении — удельную Можно показать, что молярные теплоемкости при постоянном давлении и постоянном объеме связаны уравнением Майера:
С достаточной точностью калориметрическим методом можно измерить лишь
Отношение теплоемкостей γ входит в уравнение Пуассона для адиабатического процесса:
Согласно классической теории теплоемкости идеального газа γ не зависит от температуры и однозначно определяется числом степеней свободы i его молекул. В настоящей работе для измерения γ (показателя адиабаты) применяется метод Клемана-Дезорма.
|
|
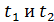 . Стрелками указаны направления движения точек струны.
. Стрелками указаны направления движения точек струны.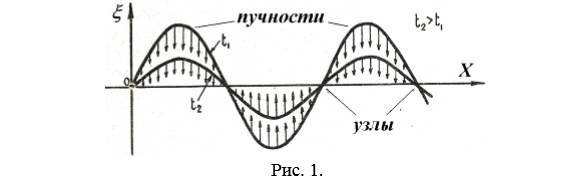
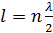 (n=1,2........). (1)
(n=1,2........). (1)
 Или
Или 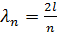 . (2)
. (2)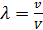 , то этим длинам волн соответствуют частоты
, то этим длинам волн соответствуют частоты  (n=0,1,2,.....). (3)
(n=0,1,2,.....). (3)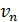 называются собственными частотами струны. Они являются кратными частоте
называются собственными частотами струны. Они являются кратными частоте , (4)
, (4) . (5)
. (5) . (6)
. (6)
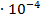
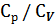 методом Клемана-Дезорма
методом Клемана-Дезорма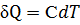 (1)
(1) (2)
(2) и молярную
и молярную  ; при постоянном объеме — удельную
; при постоянном объеме — удельную 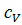 и молярную
и молярную  . Это связано с тем, что необходимое для нагревания количество теплоты зависит от условий его подвода.
. Это связано с тем, что необходимое для нагревания количество теплоты зависит от условий его подвода. (3)
(3)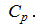 Теплоемкость газа при постоянном объеме непосредственно определить трудно, так как масса газа в нагреваемом сосуде мала по сравнению с массой калориметра, и измерения недостаточно точны. Поэтому
Теплоемкость газа при постоянном объеме непосредственно определить трудно, так как масса газа в нагреваемом сосуде мала по сравнению с массой калориметра, и измерения недостаточно точны. Поэтому 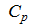 и отношение теплоемкостей:
и отношение теплоемкостей: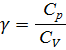
 (4)
(4)